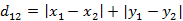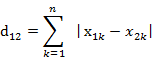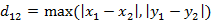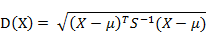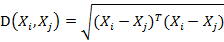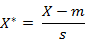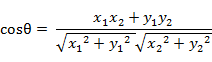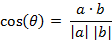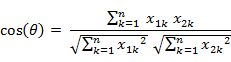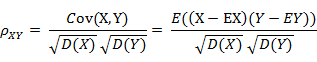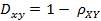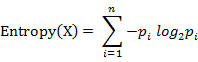统计学中相似性度量（距离）

在做分类时常常需要估算不同样本之间的相似性度量(Similarity Measurement)，这时通常采用的方法就是计算样本间的“距离”(Distance)。采用什么样的方法计算距离是很讲究，甚至关系到分类的正确与否。

而度量距离的方法有：欧式距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离、马氏距离等等。

1.欧氏距离（Euclidean Distance）

在欧几里得空间中，点x =(x1,...,xn)和 y =(y1,...,yn)之间的欧氏距离为

$d(x,y):={\sqrt {(x_{1}-y_{1})^{2}+(x_{2}-y_{2})^{2}+\cdots +(x_{n}-y_{n})^{2}}}={\sqrt {\sum _{{i=1}}^{n}(x_{i}-y_{i})^{2}}}$

向量 $\vec{x}$ 的自然长度，即该点到原点的距离为

$\|{\vec {x}}\|_{2}={\sqrt {|x_{1}|^{2}+\cdots +|x_{n}|^{2}}}$

它是一个纯数值。在欧几里得度量下，两点之间线段最短。

2. 曼哈顿距离(Manhattan Distance)

从名字就可以猜出这种距离的计算方法了。想象你在曼哈顿要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源，曼哈顿距离也称为城市街区距离(City Block distance)。

(1)二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离

(2)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的曼哈顿距离

3. 切比雪夫距离 ( Chebyshev Distance )

国际象棋玩过么？国王走一步能够移动到相邻的8个方格中的任意一个。那么国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？自己走走试试。你会发现最少步数总是max( | x2-x1 | , | y2-y1 | ) 步。有一种类似的一种距离度量方法叫切比雪夫距离。

(1)二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离

(2)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的切比雪夫距离

这个公式的另一种等价形式是

看不出两个公式是等价的？提示一下：试试用放缩法和夹逼法则来证明。

4. 闵可夫斯基距离(Minkowski Distance)

闵氏距离不是一种距离，而是一组距离的定义。

(1) 闵氏距离的定义

两个n维变量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：

其中p是一个变参数。当p=1时，就是曼哈顿距离；当p=2时，就是欧氏距离；当p→∞时，就是切比雪夫距离

根据变参数的不同，闵氏距离可以表示一类的距离。

(2)闵氏距离的缺点

　　闵氏距离，包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点。

　　举个例子：二维样本(身高,体重)，其中身高范围是150~190，体重范围是50~60，有三个样本：a(180,50)，b(190,50)，c(180,60)。那么a与b之间的闵氏距离（无论是曼哈顿距离、欧氏距离或切比雪夫距离）等于a与c之间的闵氏距离，但是身高的10cm真的等价于体重的10kg么？因此用闵氏距离来衡量这些样本间的相似度很有问题。

简单说来，闵氏距离的缺点主要有两个：(1)将各个分量的量纲(scale)，也就是“单位”当作相同的看待了。(2)没有考虑各个分量的分布（期望，方差等)可能是不同的。

5. 马氏距离(Mahalanobis Distance)

（1）马氏距离定义

       有M个样本向量X1~Xm，协方差矩阵记为S，均值记为向量μ，则其中样本向量X到u的马氏距离表示为：

       而其中向量Xi与Xj之间的马氏距离定义为：

       若协方差矩阵是单位矩阵（各个样本向量之间独立同分布）,则公式就成了：

       也就是欧氏距离了。

　　若协方差矩阵是对角矩阵，公式变成了标准化欧氏距离。

(2)马氏距离的优缺点：量纲无关，排除变量之间的相关性的干扰。

6. 标准化欧氏距离 (Standardized Euclidean distance )

(1)标准欧氏距离的定义

　　标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。标准欧氏距离的思路：既然数据各维分量的分布不一样，好吧！那我先将各个分量都“标准化”到均值、方差相等吧。均值和方差标准化到多少呢？这里先复习点统计学知识吧，假设样本集X的均值(mean)为m，标准差(standard deviation)为s，那么X的“标准化变量”表示为：

　　而且标准化变量的数学期望为0，方差为1。因此样本集的标准化过程(standardization)用公式描述就是：

　　标准化后的值 = ( 标准化前的值－分量的均值 ) /分量的标准差

　　经过简单的推导就可以得到两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的标准化欧氏距离的公式：

　　如果将方差的倒数看成是一个权重，这个公式可以看成是一种加权欧氏距离(Weighted Euclidean distance)。

7. 夹角余弦(Cosine)

有没有搞错，又不是学几何，怎么扯到夹角余弦了？各位看官稍安勿躁。几何中夹角余弦可用来衡量两个向量方向的差异，机器学习中借用这一概念来衡量样本向量之间的差异。

(1)在二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式：

(2) 两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦

类似的，对于两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)，可以使用类似于夹角余弦的概念来衡量它们间的相似程度。

　　即：

夹角余弦取值范围为[-1,1]。夹角余弦越大表示两个向量的夹角越小，夹角余弦越小表示两向量的夹角越大。当两个向量的方向重合时夹角余弦取最大值1，当两个向量的方向完全相反夹角余弦取最小值-1。

8. 相关系数 ( Correlation coefficient )与相关距离(Correlation distance)

(1) 相关系数的定义

相关系数是衡量随机变量X与Y相关程度的一种方法，相关系数的取值范围是[-1,1]。相关系数的绝对值越大，则表明X与Y相关度越高。当X与Y线性相关时，相关系数取值为1（正线性相关）或-1（负线性相关）。

(2)相关距离的定义

9.信息熵(Information Entropy)

信息熵是衡量分布的混乱程度或分散程度的一种度量。分布越分散(或者说分布越平均)，信息熵就越大。分布越有序（或者说分布越集中），信息熵就越小。

计算给定的样本集X的信息熵的公式：

参数的含义：

n：样本集X的分类数

pi：X中第i类元素出现的概率

信息熵越大表明样本集S分类越分散，信息熵越小则表明样本集X分类越集中。。当S中n个分类出现的概率一样大时（都是1/n），信息熵取最大值log2(n)。当X只有一个分类时，信息熵取最小值0

https://www.cnblogs.com/heaad/archive/2011/03/08/1977733.html