Description

​ 平面上摆放着一个n*m的点阵（下图所示是一个3*4的点阵）。Curimit想知道有多少三点组(a，b，c)满足以a，b，c三点共线。这里a，b，c是不同的3个点，其顺序无关紧要。(即(a，b，c)和
(b，c，a)被认为是相同的）。由于答案很大，故你只需要输出答案对1，000，000，007的余数就可以了。

Input

有且仅有一行，两个用空格隔开的整数n和m。

Output

有且仅有一行，一个整数，表示三点组的数目对1，000，000，007的余
数。（1，000。000。007是质数）

Sample Input

3 4

Sample Output

2 0

HINT

对于100%的数据，1< =N,m< =50000

Sol

我们可以把斜着的和横竖分开算，横竖的答案就是\(m*C(n,3)+n*C(m,3)\)，然后考虑斜着的答案：

首先斜率为正和斜率为负的方案数显然是相同的，这里只考虑斜率为正的答案。

我们枚举两端的点的横纵坐标之差\(i,j\)，然后中间整点的个数就随之确定了，然后这样的“两端的点对”的个数正是\((n-i)*(m-j)\)，中间的点个数是\(gcd(i,j)-1\)，原因看下图：

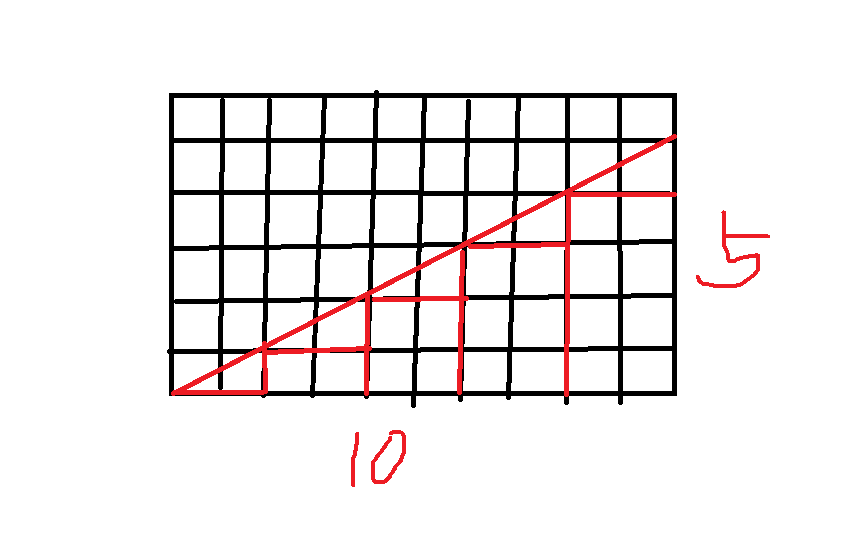
可以把原图切割成\(gcd(i,j)\)个边长为\((i/gcd(i,j),j/gcd(i,j))\)的小三角形，所以整点就有\(gcd(i,j)-1\)个。

所以得出\(ans=\sum_{i=1}^{n}\sum_{j=1}^{m}(gcd(i,j)-1)(n-i)(m-i)\)

\(=\sum_{i=1}^{n}\sum_{j=1}^{m}(n-i)(m-j)\sum_{d|gcd(i,j)}\varphi(d)-\sum_{i=1}^{n}\sum_{j=1}^{m}(n-i)(m-j)\)

假设\(n<m\)

\(=\sum_{d=1}^{n}\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{d}\rfloor}(n-id)(m-id)\varphi(d)-\sum_{i=1}^{n}\sum_{j=1}^{m}(n-i)(m-j)\)

因为\((n-id),(m-id),(n-i)(m-j)\)这些都是等差数列，能够\(O(1)\)计算，所以最终的复杂度为\(O(n)\)。

Code

#include <cstdio>
int n,m,phi[50005],vis[50005],pri[50005],tot,ans,P=1000000007;
int main()
{
    scanf("%d%d",&n,&m);if(n>m) n^=m^=n^=m;
    phi[1]=1;for(int i=2;i<=50000;i++)
    {
        if(!vis[i]) pri[++tot]=i,phi[i]=i-1;
        for(int j=1;j<=tot&&i*pri[j]<=50000;j++)
        {
            vis[i*pri[j]]=1;
            if(i%pri[j]==0){phi[i*pri[j]]=phi[i]*pri[j];break;}
            phi[i*pri[j]]=phi[i]*(pri[j]-1);
        }
    }
    for(int i=1;i<=n;i++) ans=(ans+1ll*phi[i]*(1ll*(n-i+n%i)*(n/i)/2%P)%P*(1ll*(m-i+m%i)*(m/i)/2%P)%P)%P;
    ans=(ans-1ll*(1ll*(n-1)*n/2%P)*(1ll*(m-1)*m/2%P)%P+P)%P;ans=(ans<<1)%P;
    ans=(ans+((1ll*n*(1ll*m*(m-1)*(m-2)/6)%P)+(1ll*m*(1ll*n*(n-1)*(n-2)/6%P)%P)%P)%P)%P;
    printf("%d\n",ans);
}