Algorithm——二叉搜索树
《算法导论》介绍了二叉搜索树的基本实现。二叉搜索树是一种常见的数据结构,它的定义是:“二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树”。总结地说,即在一株二叉搜索树中,对任何节点x,其左子树中的关键字最大不超过x.key,其右子树中的关键字最小不低于x.key。二叉搜索树还可以有几种常见的变形,如红黑树、B树等。
二叉查找树一般支持四种操作:
- 遍历树
- 查找树中关键字为key的节点
- 往树中插入一个关键字为key的节点
- 删除树中关键字为key的节点
删除和插入节点会改变原树的组织结构,但我们要保证操作后的新树仍满足二叉搜索书的性质。因为二叉搜索中的一个节点要记录它的key值、父节点、左孩子和又孩子节点,所以我们设计了一个数据结构来表示一个节点对象,并且约定树中不存在key值相同的节点:
/**
* 二叉搜索树中的节点对象
*
* @author coder
*
*/
class Node {
public Node(int key) {
this.key = key;
}
int key;// 节点的关键字
Node p;// 节点的父节点
Node left;// 节点的左孩子节点
Node right;// 节点的右孩子节点
}
private Node root = null;//二叉搜索树的根节点二叉搜索树性质允许我们通过一个简单的递归算法按序输出二叉搜索树中的所有关键字,这种算法称为中序遍历。它的实现是:
/**
* 中序遍历
*
* @param x
* 节点x是要开始遍历的子树的根节点
*/
public void inorderTreeWalk(Node x) {
if (x != null) {
inorderTreeWalk(x.left);
System.out.println(x.key);
inorderTreeWalk(x.right);
}
}查找一个二叉搜索树中的节点的实现也是较为简单和好理解的:
/**
* 从节点x开始,搜索一个关键字为key的节点并返回
*
* @param x
* @param k
* @return
*/
public Node treeSearch(Node x, int k) {
if (x == null || x.key == k)
return x;
if (x.key > k)
return treeSearch(x.left, k);
else
return treeSearch(x.right, k);
}查找的实现除了借助递归,也可以使用循环迭代来实现:
/*
* 搜索节点的迭代版本
*/
public Node iterativeTreeSearch(Node x, int k) {
while (x != null && x.key != k) {
if (x.key > k)
x = x.left;
else
x = x.right;
}
return x;
}在一些情况下,迭代实现可能会比递归实现效率要高。
如果我们要直接得到一株二叉搜索树中,key值最大和key值最小的节点;根据二叉搜索树的性质可知,key值最小的节点一定在左子树中,key值最大的节点一定在右子树;所以我们可以很快写出这两个操作的实现:
/*
* 根据二叉查找树的性质,key最小的节点一定在左子树中
*/
public Node treeMinimum(Node x) {
while (x.left != null)
x = x.left;
return x;
}
/*
* 根据二叉查找树的性质,key最大的节点一定在右子树中
*/
public Node treeMaximum(Node x) {
while (x.right != null)
x = x.right;
return x;
}另外二叉搜索树中还有两个概念:某个节点的后继和前驱。设一株二叉搜索中有节点x,那么节点x的前驱的定义是:所有关键字小于x.key的节点中,key值最大的那个节点;相似地,节点x的后继就是:所有关键字大于x.key的节点中,key值最小的那个节点。
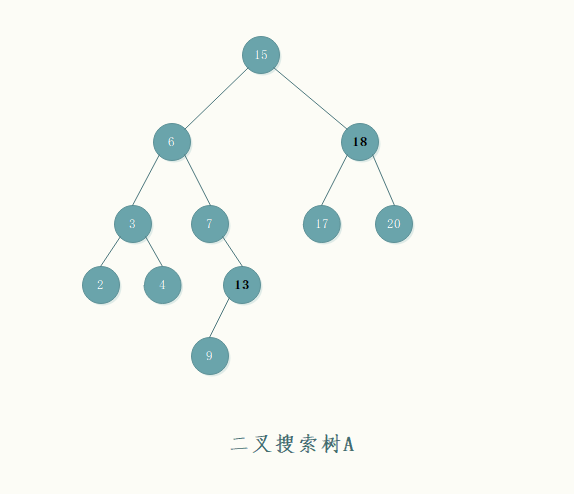
对于这样一株二叉搜索树:
如果要得到节点x的后继,那么根据二叉搜索树性质,我们分析得到:
- 如果节点x(如图中节点18)存在右子树,那它的后继一定是右子树中key最小的那个节点,也就是20
- 如果节点x不存在右子树(如图中节点13),那么它的后继需要向顶端查找,直到找到这样一个节点y:它是最靠近节点x的祖先,同时它的的左孩子也是x的一个祖先。为什么得到这样的分析呢?可知,因为节点x没有右子树,所以它的后继如果存在,则一定是在它的祖先之中;如果节点x是其父节点的左孩子,那其父节点就是它的后继;如果节点x是的其父节点的右孩子,根据二叉树搜索树性质,右子树中的节点key都会大于根节点的key,所以只能层级向上遍历,找到这样一个节点,它是节点x的祖先,同时它的左孩子也是节点x的祖先(因为根节点的值总是大于其左子树中的值,这样的节点才是x的后继)。
- 后继不存在,则返回null了
根据上面的分析,我们就可以得出获取二叉查找树某节点的后继的实现了:
/*
* 返回节点x的后继
*/
public Node treeSucCessor(Node x) {
if (x.right != null)
return treeMinimum(x.right);
Node y = x.p;
while (y != null && x == y.right) {
x = y;
y = y.p;
}
return y;
}对于某节点的前驱,它的实现思路有后继基本一致,只不过处理逻辑是相反的,它的代码如下:
/*
* 返回节点x的前驱
*/
public Node treePredeCessor(Node x) {
if (x.left != null)
return treeMaximum(x.left);
Node y = x.p;
while (y != null && x == y.left) {
x = y;
y = y.p;
}
return y;
}二叉搜索树的节点插入操作相比前两个实现会略显复杂,因为它会改变原有树的组织结构:
/*
* 二叉搜索树节点的插入操作,假设二叉搜索树中不存在key相同的节点
*/
public void treeInsert(Node z) {
Node y = null;
Node x = root;
while (x != null) {// 从根节点开始,依次比较左右节点与z的key值;找到应该在哪个子树中插入该节点
y = x;
if (z.key < x.key)
x = x.left;
else
x = x.right;
}
z.p = y;
if (y == null)// 此时树应该是空的
root = z;
else if (z.key < y.key)
y.left = z;
else
y.right = z;
}该函数的处理思路是:为了插入新节点z,我们首先要找到适合插入的子树;由二叉搜索树的性质可知,插入一个节点会导致它成为该树的一个叶子节点。从根节点root开始遍历,通过比较key值,得到待插入节点z的双亲,节点y就是记录此信息的。如果节点y为null,则说明该树本来就是一株空树,节点z插入之后,它就是根节点;如果节点z的key值比其找到的双亲小,那么节点z就应该成为节点y的左孩子;否则,它就是节点y的右孩子。
二叉查找树节点的删除处理则是最复杂的,它的代码实现逻辑分析如下:
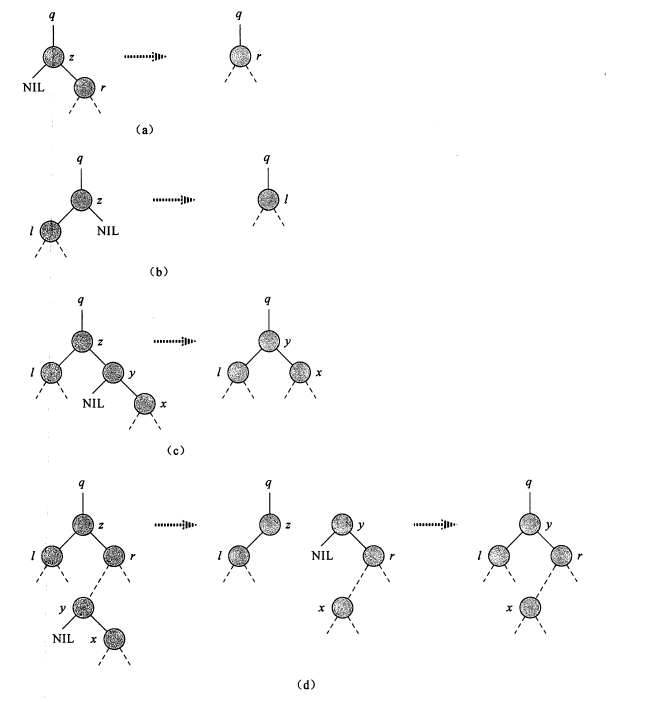
对于要删除的节点z,要考虑这么几种情况:
- 如果节点z没有孩子节点,则可以简单地将它删除;
- 如果节点z只有右孩子或者左孩子,那么就将这个孩子提升到树中z所处的位置,并修改节点z的父节点中的信息,用z的孩子节点来替换z(对应情况a、b)
- 如果节点z既有左孩子,也有右孩子;为了保持二叉搜索树的性质,我要查找z的后继y,这个后继位于z的右子树中并且没有左孩子,则需要将y移出原来的位置进行连接,并替换树中的z,具体处理为:1.如果y是z的右孩子,那么用y替换z,并仅留下y的右孩子(对应情况c);2.否则,y位于z的右子树中但并不是z的右孩子;此时,先用y的右孩子替换y,然后再用y替换z(对应情况d)
(可以给上图的四种情况中的节点标上key值以加深理解)
根据上面的分析,我们可以得出节点删除操作的代码实现是:
/*
* 二叉树节点的删除操作
*
* 1.如果z没有孩子节点,那么只是简单地将它删除,并修改它的父节点,用null最为孩子来替换z
*
* 2.如果z只有一个孩子,那么将这个孩子提升到树中z的位置,并修改z的父节点,用z的孩子来替换z
*
* 3.如果z有两个孩子,那么找z的后继y(一定在z的右子树中),并让y占据树中z的位置.z的原来右子树部分成为y的新的右子树,
* 并且z的左子树成为y的新的左子树
*/
public void treeDelete(Node z) {
if (z.left == null)
transplant(z, z.right);
else if (z.right == null)
transplant(z, z.left);
else {
Node y = treeMinimum(z.right);// y是z的后继节点
if (y.p != z) {// 如果后继节点y不是z的孩子
transplant(y, y.right);
y.right = z.right;
y.right.p = y;
}
transplant(z, y);
y.left = z.left;
y.left.p = y;
}
}
/*
* 用另一颗子树(v)替换一颗子树(u)并成为其(u)双亲的孩子节点.
*
* 调用一次transplant(n, v)时,一颗以v为根的子树来替换一颗以u为根的子树,节点u的双亲就变为节点v的双亲,并且最后v成为u的双亲的相应孩子
*/
private void transplant(Node u, Node v) {
if (u.p == null)
root = v;
else if (u == u.p.left)
u.p.left = v;
else
u.p.right = v;
if (v != null)
v.p = u.p;
此次二叉搜索树有关的源代码如下:
/**
* 二叉搜索树中的节点对象
*
* @author coder
*
*/
class Node {
public Node(int key) {
this.key = key;
}
int key;// 节点的关键字
Node p;// 节点的父节点
Node left;// 节点的左孩子节点
Node right;// 节点的右孩子节点
}
/**
*
* 二叉搜索树
*
* 设x是二叉树搜索树中的一个节点。如果y是x左子树中的一个节点,那么y.key =< x.key.如果y是x右子树中的一个节点,那么y.key >=
* x.key.
*
* @author coder
*
*/
class BinarySearchTree {
private Node root = null;// 二叉搜索树的根节点
/**
* 中序遍历
*
* @param x
* 节点x是要开始遍历的子树的根节点
*/
public void inorderTreeWalk(Node x) {
if (x != null) {
inorderTreeWalk(x.left);
System.out.println(x.key);
inorderTreeWalk(x.right);
}
}
/**
* 从节点x开始,搜索一个key值为key的节点并返回
*
* @param x
* @param k
* @return
*/
public Node treeSearch(Node x, int k) {
if (x == null || x.key == k)
return x;
if (x.key > k)
return treeSearch(x.left, k);
else
return treeSearch(x.right, k);
}
/*
* 搜索节点的迭代版本
*/
public Node iterativeTreeSearch(Node x, int k) {
while (x != null && x.key != k) {
if (x.key > k)
x = x.left;
else
x = x.right;
}
return x;
}
/*
* 根据二叉查找树的性质,key最小的节点一定在左子树中
*/
public Node treeMinimum(Node x) {
while (x.left != null)
x = x.left;
return x;
}
/*
* 根据二叉查找树的性质,key最大的节点一定在右子树中
*/
public Node treeMaximum(Node x) {
while (x.right != null)
x = x.right;
return x;
}
/*
* 返回节点x的后继
*/
public Node treeSucCessor(Node x) {
if (x.right != null)
return treeMinimum(x.right);
Node y = x.p;
while (y != null && x == y.right) {
x = y;
y = y.p;
}
return y;
}
/*
* 返回节点x的前驱
*/
public Node treePredeCessor(Node x) {
if (x.left != null)
return treeMaximum(x.left);
Node y = x.p;
while (y != null && x == y.left) {
x = y;
y = y.p;
}
return y;
}
/*
* 二叉搜索树节点的插入操作,假设二叉搜索树中不存在key相同的节点
*/
public void treeInsert(Node z) {
Node y = null;
Node x = root;
while (x != null) {// 从根节点开始,依次比较左右节点与z的key值;找到应该在哪个子树中插入该节点
y = x;
if (z.key < x.key)
x = x.left;
else
x = x.right;
}
z.p = y;
if (y == null)// 此时树应该是空的
root = z;
else if (z.key < y.key)
y.left = z;
else
y.right = z;
}
/*
* 二叉树节点的删除操作
*
* 1.如果z没有孩子节点,那么只是简单地将它删除,并修改它的父节点,用null最为孩子来替换z
*
* 2.如果z只有一个孩子,那么将这个孩子提升到树中z的位置,并修改z的父节点,用z的孩子来替换z
*
* 3.如果z有两个孩子,那么找z的后继y(一定在z的右子树中),并让y占据树中z的位置.z的原来右子树部分成为y的新的右子树,
* 并且z的左子树成为y的新的左子树
*/
public void treeDelete(Node z) {
if (z.left == null)
transplant(z, z.right);
else if (z.right == null)
transplant(z, z.left);
else {
Node y = treeMinimum(z.right);// y是z的后继节点
if (y.p != z) {// 如果后继节点y不是z的孩子
transplant(y, y.right);
y.right = z.right;
y.right.p = y;
}
transplant(z, y);
y.left = z.left;
y.left.p = y;
}
}
/*
* 用另一颗子树(v)替换一颗子树(u)并成为其(u)双亲的孩子节点.
*
* 调用一次transplant(n, v)时,一颗以v为根的子树来替换一颗以u为根的子树,节点u的双亲就变为节点v的双亲,并且最后v成为u的双亲的相应孩子
*/
private void transplant(Node u, Node v) {
if (u.p == null)
root = v;
else if (u == u.p.left)
u.p.left = v;
else
u.p.right = v;
if (v != null)
v.p = u.p;
}
}
另外,完整的测试代码如下所示:
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
Node root = new Node(12);
Node node1 = new Node(18);
Node node2 = new Node(6);
Node node3 = new Node(25);
Node node4 = new Node(7);
Node node5 = new Node(1);
// 初始化二叉搜索树
tree.treeInsert(root);
tree.treeInsert(node1);
tree.treeInsert(node2);
tree.treeInsert(node3);
tree.treeInsert(node4);
tree.treeInsert(node5);
System.out.println("中序遍历:");
tree.inorderTreeWalk(root);
System.out.println("Max key in Tree:" + tree.treeMaximum(root).key);
System.out.println("Min key in Tree:" + tree.treeMinimum(root).key);
System.out.println("node4 key=" + node4.key + "的后继:" + tree.treeSucCessor(node4).key);
System.out.println("node4 key=" + node4.key + "的前驱:" + tree.treePredeCessor(node4).key);
System.out.println("从根节点开始搜索key为" + node2.key + "的节点,它的key为:" + tree.treeSearch(root, node2.key).key);
Node node6 = new Node(5);
Node node7 = new Node(4);
System.out.println("再插入两个节点----------------------------------------------");
tree.treeInsert(node6);
tree.treeInsert(node7);
System.out.println("中序遍历:");
tree.inorderTreeWalk(root);
System.out.println("Max key in Tree:" + tree.treeMaximum(root).key);
System.out.println("Min key in Tree:" + tree.treeMinimum(root).key);
System.out.println("node2 key=" + node2.key + "的后继:" + tree.treeSucCessor(node2).key);// key为25的节点不存在后继,会抛出空指针
System.out.println("node2 key=" + node2.key + "的前驱:" + tree.treePredeCessor(node2).key);
System.out.println("删除一个节点" + node4.key);
tree.treeDelete(node4);// 删除一个节点
System.out.println("中序遍历:");
tree.inorderTreeWalk(root);
System.out.println("Max key in Tree:" + tree.treeMaximum(root).key);
System.out.println("Min key in Tree:" + tree.treeMinimum(root).key);
System.out.println("node2 key=" + node2.key + "的后继:" + tree.treeSucCessor(node2).key);// key为25的节点不存在后继,会抛出空指针
System.out.println("node2 key=" + node2.key + "的前驱:" + tree.treePredeCessor(node2).key);
}输出结果如下:
中序遍历:
1
6
7
12
18
25
Max key in Tree:25
Min key in Tree:1
node4 key=7的后继:12
node4 key=7的前驱:6
从根节点开始搜索key为6的节点,它的key为:6
再插入两个节点----------------------------------------------
中序遍历:
1
4
5
6
7
12
18
25
Max key in Tree:25
Min key in Tree:1
node2 key=6的后继:7
node2 key=6的前驱:5
删除一个节点7
中序遍历:
1
4
5
6
12
18
25
Max key in Tree:25
Min key in Tree:1
node2 key=6的后继:12
node2 key=6的前驱:5