题面

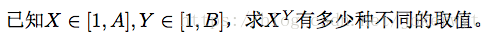
a,b <= 1e9

大佬们都说这题太显然了

我比较蒟蒻，啥想法都没有
首先观察一下，对于一个$k = x^a = y^b= p1^{e1} \cdot p2^{e2}...$，那么$lcm(a,b) |ei$。
将指数中的lcm(a,b)提出来，，$k = x0^{lcm(a,b)} = x ^ a = y ^b$。

这个形式告诉我们，对于任意被重复计算的$x^a=y^b$，我们都可以找到一个x0,使得
$x = x0^{lcm(a,b) / a}$
$y = x0^{lcm(a,b) / b}$，即x,y可以被表达为同底幂。

那么，我们要计算的实际上是同底幂的0~b次方中的重复。

用总数a * b 减去 这些重复便是答案。
对于能开根的数c，我们并不需要计算他的同底幂。 因为这些重复会在他的最简底数处计算。

那么考虑如何计算。 枚举同底c，他在1~a中的幂有$c^1,c^2...c^k$
假如k <= 1那么不需要计算，这一部分的c > $\sqrt n$，c只需要枚举到$\sqrt n$
现在问题转化为求${c^i}^y$中的重复，即$iy，i \in [1,k]，y \in [1,B]$的重复。

直接求不好搞，我们考虑分段搞。

对于区间$[(i-1)B + 1, iB]$之中的数x，假如x能整除[1,k]之间的一个数d，就一定能保证他能被分解为iy的形式吗？
显然不是
还要保证y <= b。 因此有 d >= i，即x必须要整除[i,k]这个区间内的某个数。$[(i-1)B + 1, iB]$区间具有相同特性，因此我们将它放在一起，发现这个问题只要用[i,k]中的数简单容斥一下即可求出不重个数，用kb - 不重个数即得重复个数。

但是区间内的数最多会达到30个，容斥会gg。

这时就有个trick

我们发现假如区间中有2,3,6这三个元素，那么6是不需要容斥的。 因为6的倍数能被2与3完全包含。
也即： 对于在区间中有因子的数，我们不需要加入容斥，这样的话元素的个数降到了15个。

总的时间复杂度$O(\sqrt n \cdot k \cdot 2 ^{15})$，实际上sqrt n不是满的并且 随着c的增加，k减的特别快，因此能通过本题

#include <cstdio>
#include <iostream>
#include <cstring>
#include <cmath>
using namespace std;
typedef long long ll;
ll a,b;
ll ans;
int ksm(int x,int y) {
    int ret = 1;
    for (; y; y>>=1) {
        if (y & 1) ret = ret * x;
        x *= x;
    }
    return ret;
}
ll fen;
ll gcd(ll a,ll b) {
    return b == 0 ? a : gcd(b, a % b);
}

bool isvalid(ll c) {
    int t = c, g = 0;
    for (int i = 2; i * i <= t; i ++) if (t % i == 0) {
        int u = 0; while (t % i == 0) t /= i,u++;
        g = (g == 0) ? u : gcd(u, g);
    }
    return t != 1 || g == 1;
}

int rc[30];
void init(int a,int b) {
    rc[0] = 0;
    for (int i = a; i <= b; i++) {
        int flag = 0;
        for (int j = a; j < i; j++) if (i % j == 0) {
            flag = 1; break;
        }
        if (!flag) rc[++rc[0]] = i;
    }
}

ll L, R, ret;
void dfs(int x,int xs,ll lcm) {
    if (x > rc[0]) {
        if (lcm != 0)
            ret += xs * ((R / lcm) - (L-1) / lcm);
        return;
    }
    dfs(x + 1, xs, lcm);
    dfs(x + 1, -xs, (lcm == 0) ? rc[x] : rc[x] * lcm / gcd(lcm, rc[x]));
}

int main() {
    freopen("t3.in","r",stdin);
    cin>>a>>b; ans = 1 + (a - 1) * b;
    fen = sqrt(a);
    for (ll c = 2; c <= fen; c++) {
        if (isvalid(c)) {
            int k = 0; 
            for (ll i = c; i <= a; i *= c, k++) ;
            ll s = 0;
            for (ll i = 1; i <= k; i++) { //(i-1)B+1 ~ iB
                L = (i - 1) * b + 1, R = i * b;
                init(i, k);
                ret = 0;
                dfs(1, -1, 0);
                ans -= b - ret;
            }
        }
    }
    cout<<ans<<endl;
}