原问题提出

给定一个二分类问题的训练样本集$D=\{(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),...,(\boldsymbol{x}_m,y_m)\},y_i\in \{-1, +1\}$，我们的目标是找到一条分界线/超平面来将两类区分开，如下图：

在样本空间中，超平面可以通过以下线性方程来描述：

$$\boldsymbol{w}^T\boldsymbol{x}+b=0$$
其中， $\boldsymbol{w}=(w_1,w_2,...,w_d)$为法向量，决定了超平面的方向； $b$为位移项，决定了超平面与原点的距离。

如果一个超平面能够将训练样本正确分类，则我们希望这个超平面具有的性质是，对于$(\boldsymbol{x}_i,y_i)\in D$，有

$$\boldsymbol{w}^T\boldsymbol{x}+b\left\{ \begin{aligned} >0,\ y_i=+1 \\ <0,\ y_i=-1 \end{aligned} \right.$$
这个式子也是我们在得到超平面之后预测一个新样本的判决条件。

显然，上图中 5 个超平面都满足要求。但是，哪一个是最好的呢？

直观上看，应该去找位于两类训练样本“正中间”的超平面，即上图中最粗的分界线。因为这条线能够在最大程度上容忍两类的数据波动和噪声。

因此，为了能够得到“正中间”位置的超平面，我们将上述条件变得更加严格：

$$\boldsymbol{w}^T\boldsymbol{x}+b\left\{ \begin{aligned} \ge+1,\ y_i=+1 \\ \le-1,\ y_i=-1 \end{aligned} \right. \qquad(1)$$
显然，条件严格后，靠近样本边缘的一些超平面可能会不符合要求，最后会剩下比较靠中间的几个超平面。
那么，如何选出最“正中间”的那个超平面呢？我们可以给一个具体的量化目标：让超平面与最近的样本的距离最大。

如下图所示，距离超平面最近的这几个样本点可以使得公式 (1) 的等号成立，它们被称为“支持向量”（Support Vector）。

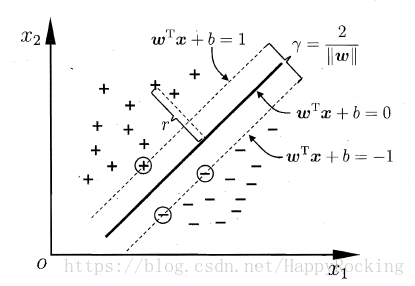
样本空间中任意点$\boldsymbol{x}$到超平面的距离的计算公式为：

$$r=\frac{|\boldsymbol{w}^T\boldsymbol{x}+b|}{||\boldsymbol{w}||}$$
因此，两类的支持向量到超平面的距离之和为
$$\gamma =\frac{2}{\boldsymbol{w}},$$
它被称为“间隔”。

如果想找到具有“最大间隔”（maximum margin）的超平面，那么需要最大化$\gamma$，也就是需要最小化$||\boldsymbol{w}||^2$。因此，最后需要求解的问题为：

$$\begin{aligned} \max_{\boldsymbol{w},b}\ &\quad \frac{1}{2}||\boldsymbol{w}||^2 \\ s.t. &\quad y_i(\boldsymbol{w}^T\boldsymbol{x}+b)\ge1,\quad i=1,2,...,m \end{aligned} \qquad (2)$$
这就是支持向量机（Support Vector Machine,SVM）的基本型。

对偶问题推导

我们希望求解问题 (2) 来得到“正中间”的分界超平面：

$$f(\boldsymbol x)={\boldsymbol w}^T\boldsymbol x + b$$
其中， $\boldsymbol w$ 和 $b$ 是模型参数，正是问题 (2) 的最优解。问题 (2) 本身是一个凸二次规划问题，可以直接使用现成的优化计算包求解。但我们有更高效的办法，即转为求解其对偶问题，转换过程如下。

根据拉格朗日乘子法，对原问题的每条约束添加拉格朗日乘子 $\alpha \ge0$，则该问题的拉格朗日函数可写为：

$$L(\boldsymbol w,b,\boldsymbol\alpha)=\frac1 2 ||\boldsymbol w||^T+\sum_{i=1}^{m}\alpha_i[1-y_i(\boldsymbol w^T\boldsymbol x_i+b)]\quad(3)$$
其中 $\boldsymbol\alpha=(\alpha_1,\alpha_2,...,\alpha_m)。$
可发现
$$\alpha_i[1-y_i(\boldsymbol w^T\boldsymbol x_i+b)]\le0$$
所以 $L(\boldsymbol w,b,\boldsymbol\alpha)\le \frac1 2 ||\boldsymbol w||^T$，即拉格朗日函数是原问题的一个下界。我们要想找到最接近原问题最优值的一个下界，就需要求出下界的最大值。

根据拉格朗日对偶性，原始问题的对偶问题是最大化最小问题：

$$\max_\alpha \min_{\boldsymbol{w},b}L(\boldsymbol w,b,\boldsymbol\alpha)$$

首先，求 $\min_{\boldsymbol{w},b}L(\boldsymbol w,b,\boldsymbol\alpha)$ ，消除掉 $\boldsymbol w,b$：分别令 $\boldsymbol w,b$ 的偏导为0，可推出

$$\begin{aligned} \frac{\partial L}{\partial \boldsymbol w}&=\boldsymbol w + \sum_{i=1}^m \alpha_i(-y_i \boldsymbol x_i)=0 \ \Rightarrow \boldsymbol w=\sum_{i=1}^m \alpha_i y_i \boldsymbol x_i\quad(4)\\ \frac{\partial L}{\partial \boldsymbol w}&= -\sum_{i=1}^m \alpha_i y_i=0 \qquad\quad\ \ \ \Rightarrow \sum_{i=1}^m \alpha_i y_i=0\ \quad(5) \end{aligned}$$
将公式（4）（5）带入到拉格朗日函数(3)，得到
$$\begin{aligned} L(\boldsymbol w,b,\boldsymbol\alpha) &=\frac1 2 ||\boldsymbol w||^T+\sum_{i=1}^{m}\alpha_i[1-y_i(\boldsymbol w^T\boldsymbol x_i+b)]\\ &=\frac1 2 \boldsymbol w^T\boldsymbol w +\sum_{i=1}^m\alpha_i -\sum_{i=1}^m\alpha_iy_i\boldsymbol x_i^T\boldsymbol w-\sum_{i=1}^m\alpha_iy_ib\\ &= \frac 1 2\boldsymbol w^T \boldsymbol w+\sum_{i=1}^m\alpha_i-\boldsymbol w^T\boldsymbol w-0\\ &=\sum_{i=1}^m\alpha_i-\frac1 2 \sum_{i=1}^m\sum_{j=1}^m \alpha_i\alpha_jy_iy_j\boldsymbol x_i^T\boldsymbol x_j^T \end{aligned}$$
因此，问题（2）的对偶问题是
$$\begin{aligned} \max_\alpha\quad &\sum_{i=1}^m\alpha_i-\frac1 2 \sum_{i=1}^m\sum_{j=1}^m \alpha_i\alpha_jy_iy_j\boldsymbol x_i^T\boldsymbol x_j^T\quad(6)\\ s.t.\quad&\sum_{i=1}^T\alpha_iy_i=0\\ &\alpha_i\ge0,i=1,2,...,m. \end{aligned}$$
解出 $\boldsymbol \alpha$ 后，求出 $\boldsymbol w$ 和 $b$ 即可得到模型：
$$\begin{aligned} f(\boldsymbol x)&=\boldsymbol w^T\boldsymbol x + b\\ &=\sum_{i=1}^m\alpha_iy_i\boldsymbol x_i^T\boldsymbol x+b \end{aligned}$$
需要注意的是，问题（2）有不等式约束，因此对偶问题需要满足KKT条件：
$$\left\{ \begin{aligned} &\alpha_i\ge0 \\ &y_if(\boldsymbol x_i)-1\ge0\\ &\alpha_i(y_if(\boldsymbol x_i)-1)=0 \end{aligned} \right.$$
因此，对于训练样本 $(\boldsymbol x_i,y_i)$，总有 $\alpha_i=0$ 或 $y_if(\boldsymbol x_i)=1$。若 $\alpha_i=0$，则该样本不会对 $f(\boldsymbol x)$ 的值有任何影响；若 $\alpha_i>0$，则必有 $y_if(\boldsymbol x_i)=1$，所对应的样本点位于最大间隔边界上，是一个支持向量。这显示出支持向量的一个重要性质：训练完成后，大部分的训练样本都不需要保留，最终模型仅与支持向量有关。