呼~好久没更了
说得根有人看似的
魔改自DZYdalao的ppt
整除和剩余
设a,b是两个整数,\(b\neq0\),则存在唯一的q和r,使得
a=qb+r,\(0 \leq r <|b|\)
即q=a/b,r=a%b
这种式子叫带余除法
若r=0,则称b整除a,记为b|a
若a和b除以m的余数相同,称为a和b模m同余,记为
\(a \equiv b (mod m)\)
在模 m 的意义下,余数相同的归为一个集合,那么所有整数被分为 m个不同的集合,模 m 的余数分别为 0,1,2,3,...,m − 1,这些集合被称为模 m 剩余类(同余类)。
一个整数的集合,对 m 取模后,余数遍历了 0,1,2,3,...,m − 1,那么该整数集合是模 m 的完全剩余系。
素数
定义:素数(质数)是大于 1 的正整数,并且除了 1 和它本身不能被其他正整
数整除。大于 1 的非素数的正整数称为合数。
素数定理:
记\(\pi(x)\)表示小于x的素数一共有多少个
那么有\(\pi(x)\approx\frac{x}{ln x}\)
这东西一般人可能证不出来
而且好像没啥用
唯一分解定理
每一个正整数都可以唯一的表示成质数的乘积,其中质数因子从小到大出现。换句话说,任意正整数 n 可以写成:
\(n = p_{1}^{a_{1}} p_{2}^{a_{2}} ... p_{k}^{a_{k}}\)
\(= \prod_{i=1}^{k} p_{i}^{a_{i}}\)
题意:
给定 X,让你构造序列 $a_{1} ,a_{2} ,...,a_{n} $,满足 \(a_{i}< a_{i+1} ,a_{i} |a _{i+1} ,a_{n} = X\)。求最大的 n,以及在最大 n 下的方案数。
把 X 质因数分解,把质因子任意排列,那么这个前缀积对应着一个最优序列。
第二问是组合数学,就不讲了
主要是不想写公式
素数筛法
由反证法,可知如果n是合数,那么它一定有一个小于\(\sqrt{n}\)的因数
可以得到以下判定法:
bool isprime(int x)
{
if (x==1)
return false;
for (int i=2;i*i<=x;i++)
if (x%i==0)
return false;
return true;
}瞎推一波可以发现,如果x是素数,那么它要么是2,要么%6=1或5
可以优化:
bool isprime(int x)
{
if (x==1)
return false;
if (x==2)
return true;
if (x%6!=1&&x%6!=5)
return false;
for (int i=2;i*i<=x;i++)
if (x%i==0)
return false;
return true;
}复杂度O(\(\sqrt{n}\))
素数筛法
如果我们想知道1~n 中所有素数,那将是O(\(n\sqrt{n}\))的
其实可以一次性把所有素数筛出来
我们可以枚举 1 到 n 所有数,如果枚举一个数的时候它没有被筛去,那么说明他是一个质数。
由调和级数,复杂度O(n ln n)
埃拉托斯特尼筛法
我们可以枚举 1 到 n 所有数,如果枚举一个数的时候它没有被筛去,那么说明他是一个质数。
对于质数,我们把大于它们且是它们倍数的数筛去。
复杂度O(n ln ln n),基本够用了
int np[MAXN],pl[MAXN],cnt;
void init()
{
np[1]=1;
for (int i=2;i<=n;i++)
if (!np[i])
{
pl[++cnt]=i;
for (int j=i*2;j<=n;j+=i)
np[i]=1;
}
}如果你觉得一堆ln碍眼你还可以自己去学一种叫欧拉筛的严格O(n)算法
题意:给定 L,R,保证$ L,R ≤ 10^{9} ,R−L ≤ 10^{5}$ ,问 [L,R] 中距离最近的两个质数的距离。
根据上面那个“如果n是合数,那么它一定有一个小于\(\sqrt{n}\)的因数”
也就是说\(\sqrt(R)\)以内的数可以筛掉[L,R]
然后瞎搞就可以了
欧拉函数
定义:\(\varphi(x)\)=1~n中与n互质的数
性质:
1.p是素数 ⇔ \(\varphi(p)\)=p-1(很好证明)
2.设 p 是一个素数,a 是一个正整数,那么
\(\varphi(p^{a}) = p^{a} - p^{a-1} = p^{a-1}(p-1)\)
也好证
3.如果 m,n 互质,那么 φ(mn) = φ(m)φ(n),这叫欧拉函数的积性。注意要互质。
可以构造一个矩阵:
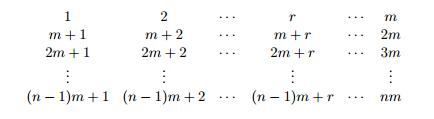
然后就可以证了
4.如果
\(n = \prod_{i=1}^{k} p_{i}^{a_{i}}\),
则
\(\varphi(n) = n \prod_{i=1}^{k} (1-\frac{1}{p_{i}}})\)
(公式挂了明天改)
可以通过意识流积性证明
5.\(\sum_{d|n} \varphi(d) = n\)
什么?证明?
你找一个n,然后把\(frac{1}{n},frac{2}{n},...,frac{n-1}{n}\)写出来,然后化成最简分数,再按分母归类,然后就会发现一件神奇的事
欧拉定理
如果 a,m 互质,那么:
\(a^{\varphi(m)} \equiv 1 (mod m)\)
证明留作课后习题略
特殊情况:费马小定理
当 p 是质数,\(a \neq p\) 时,有 \(a ^ {p-1} ≡ 1 (mod p)\)。
广义欧拉定理
若 a,m 互质,则 \(a^{n} ≡ a^{n} mod φ(m) (mod m)。\)
若 a,m 不互质,则:
\(a ^{n} ≡ a^{n} mod φ(m) (n < φ(m))\)
\(a^{n} ≡ a^{n} mod φ(m)+φ(m) otherwise\)
(例题:poj3090)[http://poj.org/problem?id=3090]
题意:
给出范围为 (0,0) 到 (n,n) 的整点,你站在原点处,问有多少个整点可见。

易知(x,y)=1
然后是个很裸的莫比乌斯反演
枚举横坐标 x,那么不被挡住的纵坐标一定与 x 互质。
ans = 2$\sum _{i=1} ^{\varphi(i)} $ + 3,3 对应 (1,0),(0,1),(0,0) 三点。
(例题:poj2720)[http://poj.org/problem?id=2720]
题意
\(f_{0} = 1,f_{i} = a^{ f_{i-1} }\),求 f_{n}的最后 7 位数 (n ≤ 100)。
啊呀atcoder要开始了,明天再写吧