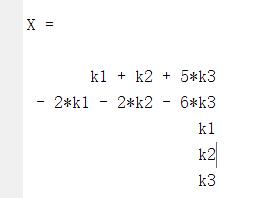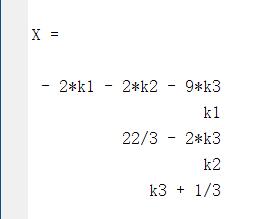常用命令
| 命令 |
功能 |
| format rat |
定义输出格式为小数分数格式 |
| A\b |
左除,求方程组的特解 |
| null(A) |
求 Ax = b 的解空间的规范正交基 |
| null(A,’r’) |
求其次线性方程组 Ax = b 的基础解系,加上 ‘r’ 求出的是一组最小正整数解 |
例1. 求齐次线性方程组的通解
用基础解系表示齐次线性方程组的通解
⎧⎩⎨⎪⎪⎪⎪x1+x2+x3+x4+x5=03x1+2x2+x3+x4−3x5=0x2+2x3+2x4+6x5=05x1+4x2+3x3+3x4−x5=0
A =[1 1 1 1 1;3 2 1 1 -3;0 1 2 2 6;5 4 3 3 -1];
format rat;
B = null(A,'r');
syms k1 k2 k3;
X = k1*B(:,1) + k2*B(:,2) + k3*B(:,3)
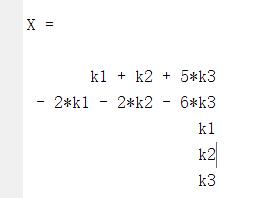
即 X = k1
⎡⎣⎢⎢⎢⎢⎢⎢1−2100⎤⎦⎥⎥⎥⎥⎥⎥
+ k2
⎡⎣⎢⎢⎢⎢⎢⎢1−2010⎤⎦⎥⎥⎥⎥⎥⎥
+ k3
⎡⎣⎢⎢⎢⎢⎢⎢5−6001⎤⎦⎥⎥⎥⎥⎥⎥
为方程式的通解,其中 k1 k2 k3 为任意实数
例2. 求非齐次线性方程组的通解
求非齐次线性方程组的通解
⎧⎩⎨⎪⎪⎪⎪2x1+4x2−x3+4x4+16x5=−2−3x1−6x2+2x3−6x4−23x5=73x1+6x2−4x3+6x4+19x5=−23x1+2x2+5x3+2x4+19x5=43
format rat;
A = [2 4 -1 4 16;-3 -6 2 -6 -23;3 6 -4 6 19;1 2 5 2 19];
b = [-2;7;-23;43];
[R,s] = rref([A,b]);
x0 = A\b;
x = null(A,'r');
syms k1 k2 k3
X = k1*x(:,1) + k2*x(:,2) + k3*x(:,3) + x0
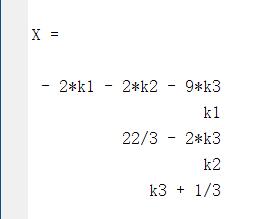
则 X = k1
⎡⎣⎢⎢⎢⎢⎢⎢−21000⎤⎦⎥⎥⎥⎥⎥⎥
+ k2
⎡⎣⎢⎢⎢⎢⎢⎢−20010⎤⎦⎥⎥⎥⎥⎥⎥
+ k3
⎡⎣⎢⎢⎢⎢⎢⎢−90−201⎤⎦⎥⎥⎥⎥⎥⎥
+
⎡⎣⎢⎢⎢⎢⎢⎢0022/301/3⎤⎦⎥⎥⎥⎥⎥⎥
为方程的通解