玩转 EM 算法

$ 参数估计 | 极大似然估计

1 参数估计的问题提出

极大似然估计：找出与 样本的分布 最接近的 概率分布模型。最大似然估计是利用已知的样本的结果，在使用某个模型的基础上，反推最有可能导致这样结果的模型参数值。

问题：假设有两点分布的抛硬币游戏，每次抛完为正面向上的概率为 $\theta$ ，则重复10次实验的得到的结果（即样本）为：+ + - + + + - + - +。
那么可得到如此结果的概率式为：

$L (θ) = θ 7 (1 - θ) 3$ $L(\theta) = \theta^7(1-\theta)^3$

能够看到这样的事件发生，我们就认为背后的这套概率模型机制发生的概率最大。于是求如上的概率公式 $L(\theta)$ 的最大值（转化为对数然后对 $\theta$ 求导）。

2 极大似然估计

求最大似然函数估计值的一般步骤：

（1）写出似然函数；

（2）对似然函数取对数，并整理；

（3）对参数求导，令导数为0，得到似然方程；

（4）解似然方程，得到的参数即为所求；

3 为什么要有 EM ？

但是当概率模型含有隐变量时，就没有办法直接使用极大似然估计方法，从而提出能够求解隐变量的 EM 算法。

参考文献：https://www.jianshu.com/p/1121509ac1dc

扫描二维码关注公众号，回复： 3091105 查看本文章

后面在GMM模型中也会再次说明。

$ 凸优化 | Jensen 不等式

1 凸函数定义

给定映射 $f:\mathbb{R}^n \rightarrow \mathbb{R}$ ，如果 $\mathbf{dom }\ f \subseteq \mathbb{R}^n$ 为凸集，并且对于任意 $x,y \in \mathbf{dom }\ f$ 和任意 $0 \leq t \leq 1$ ，满足

$f (t x + (1 - t) y) \leq t f (x) + (1 - t) f (y)$ $f(tx+(1-t)y) \leq tf(x)+(1-t)f(y)$
则称函数是凸的。
如下图所示，凸函数特点：弦在弧上！

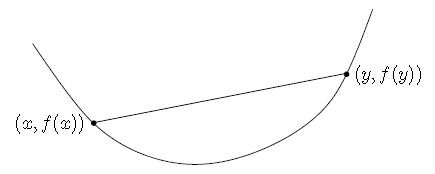
2 Jensen 不等式

Th1：如果 $f$ 是凸函数， $X$ 是随机变量，则：

$f (E (X)) ⩽ E (f (X))$ $f(\mathbb{E}(X)) \leqslant \mathbb{E}(f(X))$
特别地，如果 $f$ 是严格凸函数，那么 $f(\mathbb{E}(X)) = \mathbb{E}(f(X))$ 当且仅当 $X$ 是常量，即 $p(x=\mathbb{E}(X))=1$ 。

Th2：若 $f$ 是凹函数，则：

$f (E (X)) \geq E (f (X))$ $f(\mathbb{E}(X)) \ge \mathbb{E}(f(X))$

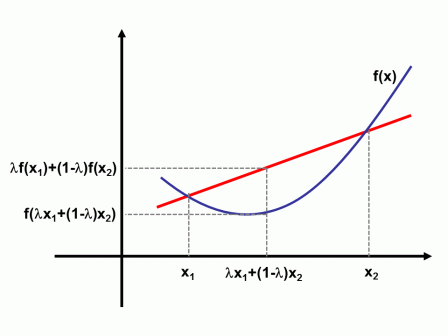
严格凸：对于任意 $\color{red} {x \neq y}$ ，且 $0<t<1$ ，有

$f (t x + (1 - t) y) < t f (x) + (1 - t) f (y)$ $f(tx+(1-t)y)\color{red} {<}tf(x)+(1-t)f(y)$

$ EM算法 | GMM模型

1 EM算法的要点

简介：
…………………………………………………………………………………………
《数学之美》的作者吴军将EM算法称为上帝的算法，EM算法也是公认的机器学习十大经典算法之一。
…………………………………………………………………………………………
EM是一种求解参数极大似然估计的迭代算法，具有良好的收敛性和每次迭代都能使似然函数值单调不减的优良性质。
…………………………………………………………………………………………
在统计学习、NLP 等领域应用非常广泛，许多统计学算法都是 EM 算法的体现，如隐马尔科夫模型的训练方法 Baum-Welch 算法、最大熵模型的训练方法 GIS 算法、高斯混合模型 EM 算法、主题模型训练推理的 pLSA 方法，都属于 EM 算法。甚至连聚类中的 k-means 算法其实也是EＭ方法的体现。

上面的简介在我看来就是激发一下兴趣，不过本质就是废话！接下来我们看几个要点，理解算法的灵魂核心。在我看来，EM算法就是条件概率的一场游戏。

要点 1 ：隐变量的华丽登场

似然估计的概率公式为 $L(\theta)$ ，其中 $y_i$ 是样本数据（观测值），公式中可能会有隐变量 $z$ ，公式变为 $p(y,z)$ 。

公式可以根据强行分离出隐变量 $z$ 的形式：联合分布再积分。

L (θ) = \prod i = 1 m p (y i | θ) = \prod i = 1 m [\sum z p (y i, z | θ)]

$L(\theta)=\prod_{i=1}^mp(y_i|\theta)=\prod_{i=1}^m\left[\sum_z p(y_i,z|\theta)\right]$

取对数：要注意隐含变量其实是 $z^{(i)}$ 。

ℓ (θ) = \sum i l o g p (y i | θ) = \sum i l o g \sum z p (y i, z | θ)

$\ell(\theta) = \sum_{i}\mathbf{log}\, p(y_i|\theta)= \sum_{i}\mathbf{log}\sum_zp(y_i,z|\theta)$

\sum i l o g \sum z p (y i, z | θ) = \sum i l o g \sum z (i) p (y i, z (i) | θ)

$\sum_{i}\mathbf{log}\sum_zp(y_i,z|\theta) = \sum_{i}\mathbf{log}\sum_{z^{(i)}}p(y_i,z^{(i)}|\theta)$

对于每一个样例 $y_i$ ，令 $Q_i$ 表示该样例隐变量 $z$ 的某种分布。

$Q_i$ 满足的条件是 $\sum_{z^{(i)}} Q_i(z^{(i)})=1,Q_i(z^{(i)})>0$ 。

\sum z p (y i, z (i) | θ) = \sum z Q i (z (i)) p ( y i , z ( i ) | θ ) Q i ( z ( i ) )

$\sum_z p(y_i,z^{(i)}|\theta)= \sum_z Q_i(z^{(i)}) \frac{p(y_i,z^{(i)}|\theta)}{Q_i(z^{(i)})}$

ℓ (θ) = \sum i l o g \sum z p (y, z | θ) = \sum i l o g \sum z Q i p ( y , z | θ ) Q i

$\ell(\theta) = \sum_{i}\mathbf{log}\sum_zp(y,z|\theta)= \sum_{i}\mathbf{log}\sum_zQ_i \frac{p(y,z|\theta)}{Q_i}$

要点 2 ：Jensen不等式的应用

$\mathbf{log}$ 是凹函数。因此有

$l o g (E (X)) \geq E (l o g (X))$ $\mathbf{log}(\mathbb{E}(X)) \ge \mathbb{E}(\mathbf{log}(X))$
$X$ 可以替换为下面的表达式：
$p ( y , z | θ ) Q i$ $\frac{p(y,z|\theta)}{Q_i}$

l o g \sum z Q i p ( y , z | θ ) Q i \geq \sum z Q i [l o g p ( y , z | θ ) Q i]

$\mathbf{log}\sum_zQ_i \frac{p(y,z|\theta)}{Q_i} \geq \sum_z Q_i [\mathbf{log} \frac{p(y,z|\theta)}{Q_i}]$

ℓ (θ) = \sum i l o g \sum z Q i p ( y , z | θ ) Q i \geq \sum i \sum z Q i l o g p ( y , z | θ ) Q i

$\ell(\theta) = \sum_{i}\mathbf{log}\sum_zQ_i \frac{p(y,z|\theta)}{Q_i} \geq \sum_{i}\sum_z Q_i \mathbf{log} \frac{p(y,z|\theta)}{Q_i}$

要点 3 ：探索最紧的下界

特别地如果 $f(\mathbb{E}(X)) = \mathbb{E}(f(X))$ 当且仅当 $X$ 是常量，即

$p ( y , z | θ ) Q i = c$ $\frac{p(y,z|\theta)}{Q_i} = c$
$c$ 是 constant ，则有
$ℓ (θ) = \sum i l o g \sum z Q i p ( y , z | θ ) Q i = \sum i \sum z Q i l o g p ( y , z | θ ) Q i$ $\ell(\theta) = \sum_{i}\mathbf{log}\sum_zQ_i \frac{p(y,z|\theta)}{Q_i} \color{red}{=} \sum_{i}\sum_z Q_i \mathbf{log} \frac{p(y,z|\theta)}{Q_i}$
$Q_i$ 满足的条件是 $\sum_{z^{(i)}} Q_i(z^{(i)})=1,Q_i(z^{(i)})>0$ 。

Q i (z (i)) = p ( y , z ( i ) | θ ) c = p ( y , z ( i ) | θ ) \sum z p ( y , z | θ ) = p (z (i) | y, θ)

$Q_i(z^{(i)}) = \frac{p(y,z^{(i)}|\theta)}{c}= \frac{p(y,z^{(i)}|\theta)}{\sum_z p(y,z|\theta)}= p(z^{(i)}|y,\theta)$

要点 4 ：EM 算法框架

初始化分布参数 $θ$ ；重复E、M步骤直到收敛：

E 步：根据参数 $θ$ 初始值或上一次迭代所得参数值来计算出隐变量的后验概率（即隐性变量的期望），作为隐性变量的现估计值：

$Q i (z (i)) = p (z (i) | y i, θ)$ $Q_i(z^{(i)}) = p(z^{(i)}|y_i,\theta)$
M 步：将似然函数最大化以获得新的参数值 $θ$ ：
$θ = a r g m a x θ \sum i \sum z Q i l o g p ( y , z | θ ) Q i$ $\theta=\underset{\theta}{argmax} \sum_{i} \sum_z Q_i \mathbf{log} \frac{p(y,z|\theta)}{Q_i}$

2 GMM模型

问题 1 ：高斯分布

随机挑选10000名志愿者，测量身高。
志愿者中分男性和女性：男性身高分布服从 $\mathcal N(\mu_1 ,\sigma_1)$ ，女性身高分布服从 $\mathcal N(\mu_2 ,\sigma_2)$ 。
在样本中未知样本属于男性还是女性，即打乱样本的情况下，参数估计 $\mu_1 ,\sigma_1,\mu_2 ,\sigma_2$ 。
如果将两个二维高斯分布 $\mathcal{N}(\boldsymbol{\mu_1}, \boldsymbol{\Sigma}_1)$ 和 $\mathcal{N}(\boldsymbol{\mu_1}, \boldsymbol{\Sigma}_1)$ 合成一个二维的分布，那么就可以用合成后的分布来描述所有点。最直观的方法就是对这两个二维高斯分布做线性组合，用线性组合后的分布来描述整个集合中的数据。这就是高斯混合模型（GMM）。

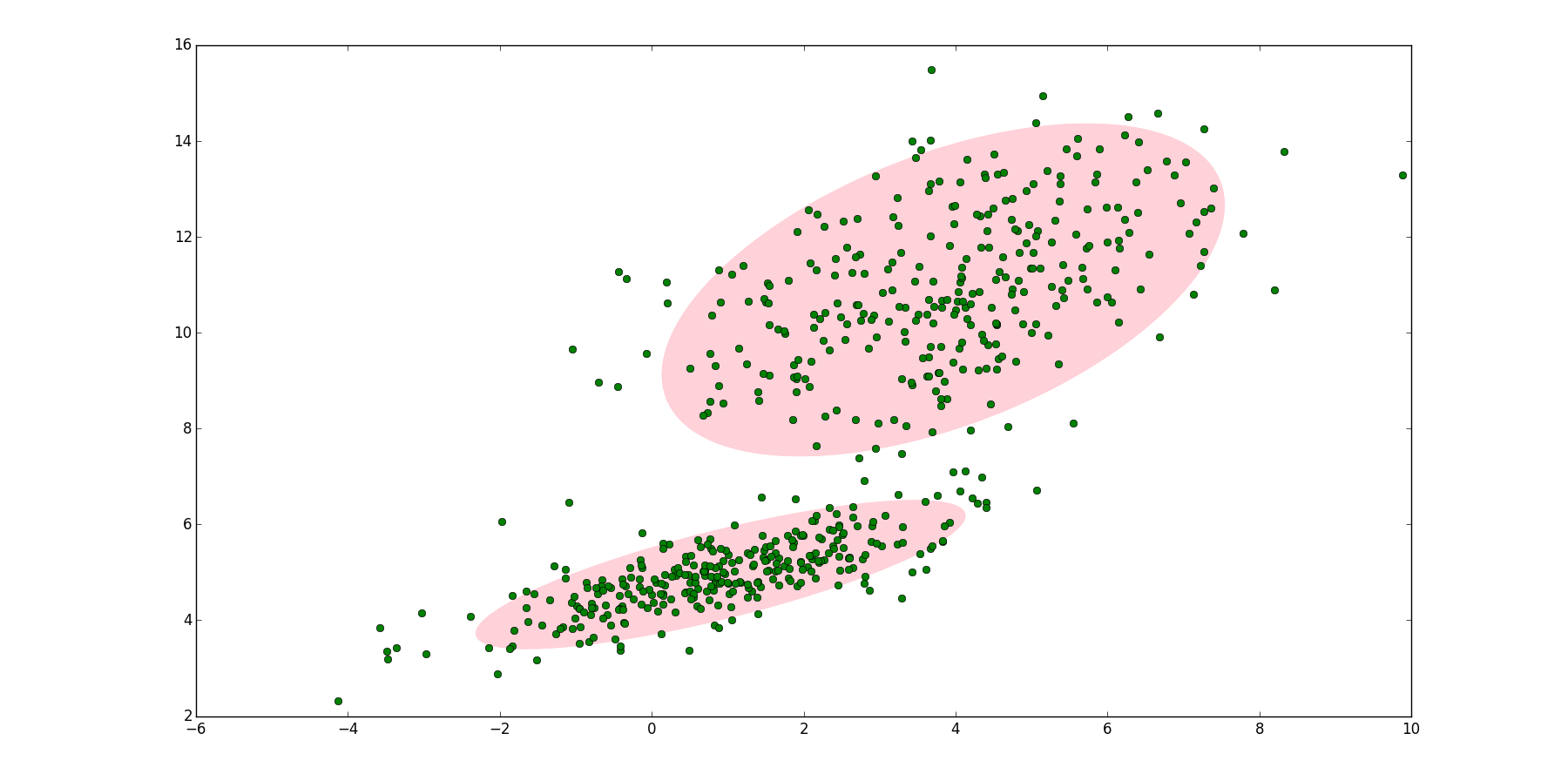
参考文献：http://blog.csdn.net/jinping_shi/article/details/59613054

问题 2 ：GMM 的参数

GMM模型中有三个参数需要估计，分别是 $\boldsymbol{\pi},\boldsymbol{\mu},\boldsymbol{\Sigma}$ 。这里的参数都是以矩阵或者向量的形式出现。
参考文献：http://blog.csdn.net/u012151283/article/details/77649924

假设数据服从 $K$ 个混合高斯分布。即数据能够由 $K$ 个确定的高斯分布以一定的权重叠加生成。

$\pi_k$ 是选中参量为 $\mu_k$ 和 $\Sigma_k$ 的概率，也叫权值因子：

\sum K π k = 1

$\sum_K \pi_k = 1$

从数据集求出这 $K$ 个高斯分布的参数：假设 $K=2$ ，那么对应的 GMM 形式如下：

p (x) = π 1 N (x | μ 1, Σ 1) + π 2 N (x | μ 2, Σ 2)

$p(\boldsymbol{x}) =\pi_1 \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_1, \boldsymbol{\Sigma}_1) + \pi_2 \mathcal{N}(\boldsymbol{x}|\boldsymbol{\mu}_2, \boldsymbol{\Sigma}_2)$
通过 EM 算法，我们可以迭代计算出GMM中的参数：

(π k, x k, Σ k)

$(\pi_k, \boldsymbol{x}_k, \boldsymbol{\Sigma}_k)$
参考文献：http://blog.csdn.net/junshen1314/article/details/50300421

问题 3 ：GMM 的 EM 应用

step 1：定义分量数目 $K$ ，对每个分量 $k$ 设置 $\pi_k，μ_k，\Sigma_k$ 的初始值，然后计算对数似然函数：
$p (x i | π, μ, Σ) = \sum k = 1 K π k N (x i | μ k, Σ k)$ $p(\boldsymbol{x_i}|\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \sum_{k=1}^K\pi_k \mathcal{N}(\boldsymbol{x_i}|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)$
$log \prod i p (x i | π, μ, Σ) = \sum i log p (x i | π, μ, Σ)$ $\log\prod_{i} p(\boldsymbol{x_i}|\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \sum_{i} \log p(\boldsymbol{x_i}|\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma})$

E step：根据当前的 $\pi_k，μ_k，\Sigma_k$ 计算后验概率，即期望 $\gamma(n,k)$ ：
$γ (n, k) = π k N ( x n | μ n , Σ n ) \sum K j = 1 π j N ( x n | μ j , Σ j )$ $\gamma(n,k) = \frac{\pi_k\mathcal{N}(\boldsymbol{x}_n| \boldsymbol{\mu}_n, \boldsymbol{\Sigma}_n)}{\sum_{j=1}^K \pi_j \mathcal{N}(\boldsymbol{x}_n| \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)}$
$\gamma(n,k)$ 可以认为是第 $n$ 个样本来自第 $k$ 个分布的概率。

M step：根据 E step 中计算的 $\gamma(n,k)$ 再计算新的 $\pi_k，μ_k，\Sigma_k$ ：
$μ n e w k Σ n e w k π n e w k = 1 N k \sum n = 1 N γ (n, k) x n = 1 N k \sum n = 1 N γ (n, k) (x n - μ n e w k) (x n - μ n e w k) T = N k N$ $\begin{split} \boldsymbol{\mu}_k^{new} &= \frac{1}{N_k} \sum_{n=1}^N \gamma(n,k) \boldsymbol{x}_n \\ \boldsymbol{\Sigma}_k^{new} &= \frac{1}{N_k} \sum_{n=1}^N \gamma(n,k) (\boldsymbol{x}_n - \boldsymbol{\mu}_k^{new}) (\boldsymbol{x}_n - \boldsymbol{\mu}_k^{new})^T \\ \pi_k^{new} &= \frac{N_k}{N} \end{split}$
其中的 $N_k = \sum_{n=1}^N \gamma(n,k)$

step 4：计算对数似然函数：
$log p (x | π, μ, Σ) = \sum n = 1 N log {\sum k = 1 K π k N (x k | μ k, Σ k)}$ $\log p(\boldsymbol{x}|\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \sum_{n=1}^N \log \left\{\sum_{k=1}^K \pi_k \mathcal{N}(\boldsymbol{x}_k| \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)\right\}$

step 5：检查参数是否收敛或对数似然函数是否收敛，若不收敛，则返回第 2 步。

以上关于 GMM 的参数估计推导可以类比 EM 推导。