乘法逆元

就是 $a\times b\equiv 1(\mod p\left\left\left)$

此时b就是a模p意义下的逆元，即 $inv[a]=b;$

下面我们用inv[a]表示a模p意义下的逆元。

逆元是好东西啊

有时候我们需要算出 a/b mod p 的值，用朴素的方法，我们只能在 a 上不断加 p ，直到它能被 b 整除为止。
当 a,b,p 都很大的时候，这种方法就只能凉凉了，但如果有了逆元，我们就可以非常方便，快捷地求解。                    

                                                                      ——————某位大佬的话

所以我先讲讲逆元性质：

唯一性就不用讲了

1.积性

假如a与b互质， $inv[a]\times inv[b]\equiv inv[a*b]$

2.乘变除

$a\times inv[b]\equiv a\div b (\mod p\left\left)$

证明如下：

$b\times inv[b]\equiv 1\left ( \mod p \left\left)$

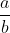两边都乘一个 $\frac{a}{b}$ ,就得到了上面的式子

至于逆元的求法，有很多，我只讲四种。

首先，是求单个逆元

1.费马小定理

当 p 为素数时：

$a^{p-1}\equiv 1(\mod p\left\left\left)$

$a^{p-1}= a\times a^{p-2}$

所以

$a\times a^{p-2}\equiv 1(\mod p\left\left\left)$

所以 $a^{p-2}$ 就是a在模p意义下的逆元，快速幂求出 $a^{p-2}$ 即可。

此方法的局限就是p只能是质数。

int ksm(int t)
{
    if(t==1)return n%p;
    if(t%2==0)
    return ksm(t>>1)*ksm(t>>1)%p;
    else
    return ksm(t>>1)*ksm(t>>1)*(n)%p;
}
int main()
{
    scanf("%d%d",&n,&p);
    printf("%d",ksm(p-2));
}

2.扩展欧几里得

$a\times inv[a]\equiv 1(\mod p\left\left\left)$

变一下，我们把p移到左边就成了

$a\times inv[a]-py= 1$

因为y是变量所以可以变成这样：

$a\times inv[a]+py= 1$

我们把 $inv[a]$ 设成x，就变成了扩欧的标准式：

$ax+py= 1$

就可以瞎搞了，至于不知道怎么瞎搞的同学，可以先点这里exgcd入门以及同余基础

inline void exgcd(ll a,ll b)
{
    if(!b)
    {x=1;y=0;return;}
    exgcd(b,a%b);
    k=x;x=y;
    y=k-a/b*y;
    return;
}
int main()
{
    scanf("%d%d",&n,&p);
    exgcd(n,p);
    printf("%d",x);
}

然后，就是求多个逆元

1.欧拉函数筛法

在数论，对正整数n，欧拉函数是小于或等于n的正整数中与n互质的数的数目（φ(1)=1）。
                                                         ——————百度百科

我们设 $\varphi(x)$ 表示小于等于x且与x互质的正整数的个数。

通式如下：

还有欧拉函数有如下几点性质：

欧拉函数是积性函数——若m,n互质，
假如n为奇数，
假如n为质数，

欧拉函数与费马小定理有点~~不明不白的~~关系

对任何两个互质的正整数a, m(m>=2)有

这就是欧拉定理

所以类比于费马小定理的证法：

$a^{\phi\left (m \right )}\equiv 1(\mod p\left\left\left)$

$a^{\phi\left (m \right )}= a\times a^{\phi\left (m \right )-1}$

所以 $a\times a^{\phi(m)-1} \equiv 1(\mod p\left\left\left)$

所以我们要求的就是 $a^{\phi(m)-1}$ ，又因为欧拉函数是积性函数，所以把m筛一下质数就好了。

不过有更好的办法，这里就不写代码了（~~其实不会~~）

2.线性递推

证明好麻烦啊，~~那就不证了~~

反正就是设 $p= b\times k+a$ ；

再往 $a\times inv[a]\equiv 1(\mod p\left\left\left)$ 代

最后得出： $-(\frac{p}{a})*inv[p\mod a]\equiv inv[a]$

讲完了，现在讲题目

我要讲洛谷的两道题：

1.P3811

这就是模板题，直接套线性递推，就能ac了

int main()
{
    int n,m;
    read(n),read(m);
    inv[1]=1;
    for(register int i=2;i<=n;i++)
    inv[i]=(long long)(m-m/i)*inv[m%i]%m;\\加一个m是为了去负
    for(register int i=1;i<=n;i++)
    printf("%d\n",inv[i]);
}

值得一提的是，这题扩欧卡一卡也可以过（好水）

long long k,x,y;
inline void read(long long &x)
{
    x=0; 
    int f=1; 
    char ch=getchar();
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') 
        f=-1; 
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }x*=f;
}
inline void exgcd(int a,long long b)
{
    if(b==0)
    {x=1;y=0;return;}
    exgcd(b,a%b);
    k=x;x=y;
    y=k-a/b*y;
    return;
}
int main()
{
    long long n,m;
    read(n),read(m);
    for(register int i=1;i<=n;i++)
    {
        exgcd(i,m);
        if(x<=0)x+=m;
        printf("%lld\n",x);
    }
}

对了，还有一个，费马小定理算法。

得分48，a了3个，t了3个

inline long long ksm(int t,int i)//记得开long long不然第三个点会wa
{
    if(t==1)return i%m;
    if(t%2==0)
    return ksm(t>>1,i)*ksm(t>>1,i)%m;
    else
    return ksm(t>>1,i)*ksm(t>>1,i)*(i)%m;
}
int main()
{
    long long n;
    io::begin();
    io::read(n);
    io::read(m);
    for(register int i=1;i<=n;i++)
    printf("%lld\n",ksm(m-2,i));
}

但是我发现，去掉 inline，就a了4个点，得分64.

所以给大家一个忠告，在递归函数下，inline不是一个好的卡常方法！

因为使用内联函数后虽然调用函数的开销降低了，但是有利必有弊，内联函数会导致主函数指令增多、函数体积增大等情况。

这题就这样

2.P2613

一看数据范围还是很吓人的， $10^{10001}$ ，怕不是要打高精，后来发现不是这样，不过题解中真有高精算法，大佬！！

首先，先看我最开始引用的话，嗯，有点道理

$\frac{a}{b}=a\times b^{-1}$

$b \times b^{-1}=1$

所以在模p意义下所以 $b^{-1}$ 可以用inv[b]代替。

所以扩欧一遍过（29ms），只是读入时注意一下边读边模就好了；

inline void exgcd(int a,int b)
{
    if(!b)
    {x=1;y=0;pos=a;return;}
    exgcd(b,a%b);
    k=x;x=y;
    y=k-a/b*y;
    return;
}
int main()
{
    std::cin>>a1>>b1;
    int n=0,m=0;
    for(register int i=0;i<strlen(a1);i++)
    n=(n*10+a1[i]-48)%mod;
    for(register int i=0;i<strlen(b1);i++)
    m=(m*10+b1[i]-48)%mod;
    exgcd(m,mod);
    if(pos!=1)printf("Angry!");
    else
    {
        if(x<0)x+=mod;
        printf("%lld",(1ll*n*x)%mod);
    }
}

这道题，模数很暴力（是质数），所以，可以用快速幂，速度比exgcd慢不了多少（32ms）

#define mod 19260817
#define maxn 10100
using namespace std;
char a1[maxn],b1[maxn];
inline long long ksm(long long x,long long y)
{
    long long ans=1;
    while(y)
    {
        if(y&1)ans*=x,ans%=mod;
        x*=x,x%=mod;y>>=1;
    }return ans%mod;
}
int main()
{
    cin>>a1>>b1;
    int n=0,m=0;
    for(int i=0;i<strlen(a1);i++)
    n=(n*10+a1[i]-48)%mod;
    for(int i=0;i<strlen(b1);i++)
    m=(m*10+b1[i]-48)%mod;
    if(m==0)printf("Angry!");
    else printf("%lld",(1ll*n*ksm(m,mod-2))%mod);
}

最后通过这道题的大质数给大家念一首诗：~~苟利国家生死以~~

乘法逆元及两道模板题详解

1.积性

2.乘变除

$a\times inv[b]\equiv a\div b (\mod p\left\left)$

两边都乘一个 $\frac{a}{b}$ ,就得到了上面的式子

首先，是求单个逆元

1.费马小定理

2.扩展欧几里得

然后，就是求多个逆元

1.欧拉函数筛法

2.线性递推

但是我发现，去掉 inline，就a了4个点，得分64.

所以给大家一个忠告，在递归函数下，inline不是一个好的卡常方法！

因为使用内联函数后虽然调用函数的开销降低了，但是有利必有弊，内联函数会导致主函数指令增多、函数体积增大等情况。

猜你喜欢

乘法逆元及两道模板题详解

1.积性

2.乘变除

两边都乘一个 ,就得到了上面的式子

首先，是求单个逆元

1.费马小定理

2.扩展欧几里得

然后，就是求多个逆元

1.欧拉函数筛法

2.线性递推

但是我发现，去掉 inline，就a了4个点，得分64.

所以给大家一个忠告，在递归函数下，inline不是一个好的卡常方法！

因为使用内联函数后虽然调用函数的开销降低了，但是有利必有弊，内联函数会导致主函数指令增多、函数体积增大等情况。

猜你喜欢

两边都乘一个 $\frac{a}{b}$ ,就得到了上面的式子