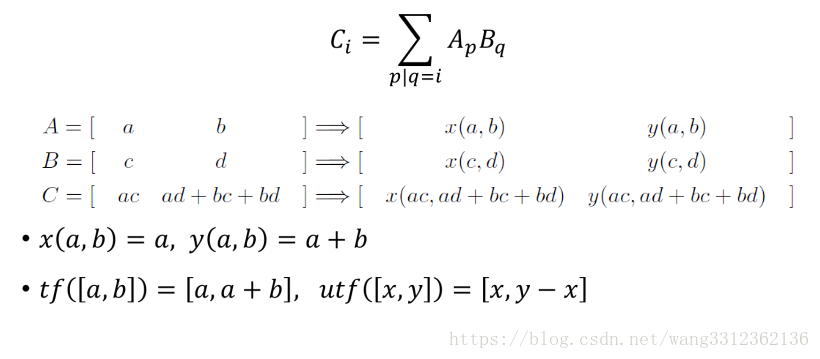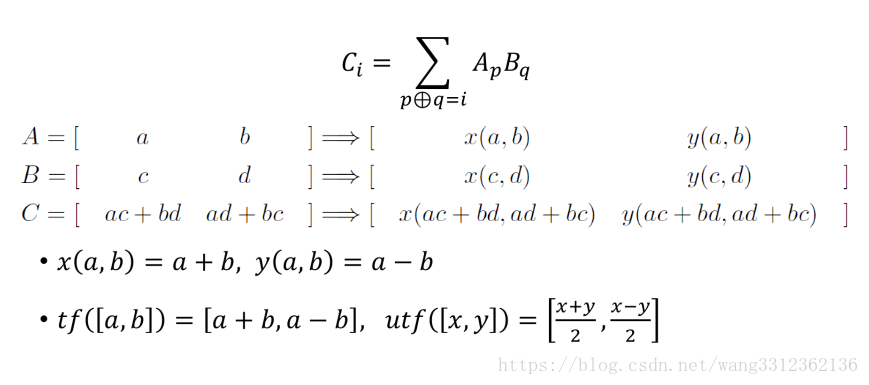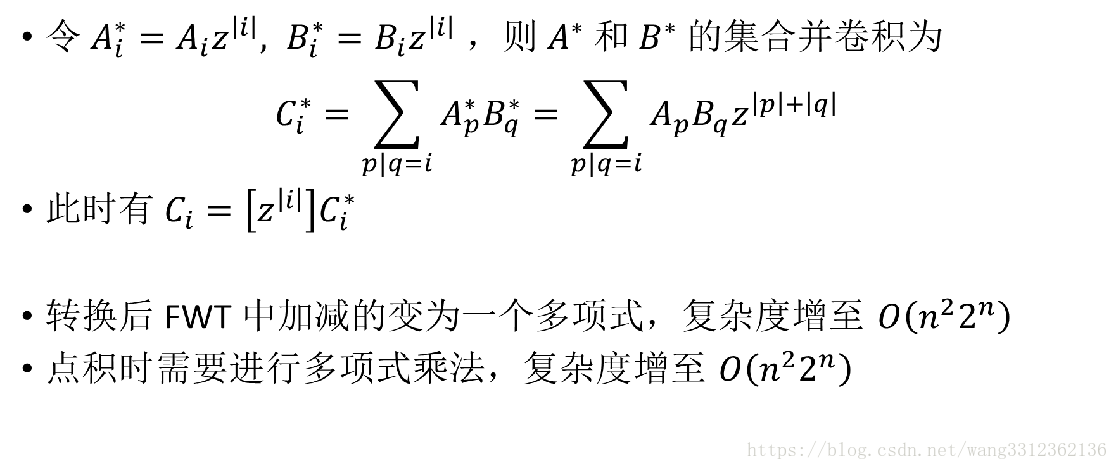从多项式乘法到FFT

这一段大部分是复制以前我写的这篇博客：

https://blog.csdn.net/wang3312362136/article/details/79510933

这篇博客有详细的代码，但是阅读体验布星，因此我把它的大部分证明过程复制下来。

如果会fft，请跳过这一段。

多项式乘法

我们知道，多项式可以表示成：

$$A=\sum_{i=0}^{n}a_ix^i$$ 的形式。

对于两个多项式$A(x)$和$B(x)$，我们可以计算乘积$A\cdot B$：

$$A\cdot B=\sum_{i=0}^{|A|}\sum_{j=0}^{|B|}a_ib_jx^{i+j}$$

但是，这样算是$O(|A|\times |B|)$的，太慢了，怎么办？

我们需要换一条思路。

首先，我们得知道一个东西：多项式的点值表示法。

我们把上面的称为多项式的系数表示法，而点值表示法就是：

若$A$多项式的次数为$n$，则任取$n$个不相同的$x_0,x_1,\cdots,x_n$，求出$A$多项式的$A(x_0),A(x_1),\cdots,A(x_n)$。记为：

$$<(x_0,A(x_0)),(x_1,A(x_1)),\cdots,(x_n,A(x_n))>$$

显然，一个有$n+1$个点的点对唯一表示一个$n$次多项式。

对于一个点值表示法下多项式

$$<(x_0,A(x_0)),(x_1,A(x_1)),\cdots,(x_n,A(x_n))>$$

和

$$<(x_0,B(x_0)),(x_1,B(x_1)),\cdots,(x_n,B(x_n))>$$

它们的乘积是

$$<(x_0,A(x_0)\cdot B(x_0)),(x_1,A(x_1)\cdot B(x_1)),\cdots,(x_n,A(x_n)\cdot B(x_n))>$$

可以看出点值表示法的多项式相乘是$O(n)$的。

等等，我们好像找到了一个突破口！

为啥不把原来的系数表示法下的多项式转化成点值表示法呢？

仔细想一想：系数表示法与点值表示法互相转换，这个步骤好像是$O(n^2)$的。

而FFT（快速傅里叶变换）就是为了优化这个$O(n^2)$。

PS：对于$O(n^2)$的点值表示法转化成系数表示法可以看百度百科中关于插值法的介绍。

FFT（快速傅里叶变换）

如果未特别说明，那么下面的多项式次数将是$2^k-1$的形式。

如果不是关键部分的公式或定理，不提供证明，自己出门右转百度。

首先介绍两个概念：

DFT（离散傅里叶变换）是将多项式由系数表示法转化成点值表示法；

IDFT（离散傅里叶逆变换）是将多项式由点值表示法转化成系数表示法；

而FFT就是上述两种变换的优化。

DFT部分

前置技能：

下面的内容将会提到复数，不会的可以参考百度百科中关于复数的介绍；

为了介绍FFT中的DFT部分，首先要介绍的是一个概念：单位根。

单位根：若有

$$z^n=1$$ 此时将 $z$称为 $n$次单位根。

若有$z\in \mathbb R$，显然，$z$可以等于$1$，如果$n$是偶数，则$z$还可以等于$-1$。

我们把范围扩大到$z \in \mathbb C$，那么，我们可以得到$n$个复数，它们将复平面上的单位圆等分成$n$份。

为了表示$n$次单位根，我们引入一个公式。

欧拉公式：

$$e^{in}=\cos n+i\sin n$$

如果我们令：

$$\omega_n=e^{2\pi i/n}$$

那么，$n$次单位根就可以表示成$\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}$，它们的$n$次方显然都是$1$。

下面是关于$\omega_n$的两条性质：（都是在$n$为偶数的情况下）

$$\omega_n^{n/2}=e^{(2\pi i/n)\cdot (n/2)}=e^{\pi i}=cos \pi+i\sin \pi=-1\tag{1}$$

$$\omega_n^2=e^{2\cdot 2\pi i/n}=\omega_{n/2}\tag{2}$$

下面，我们进入正题：DFT的求法。

在这里，我们令多项式次数为$n-1$，那么我们可以用点值表示成

$$<(\omega_n^0,A(\omega_n^0),(\omega_n^1,A(\omega_n^1)),\cdots,(\omega_{n}^{n-1},A(\omega_n^{n-1}))>$$

额……这时间复杂度好像并没有减少……
别急，我们来看$A(\omega_n^k)$能够表示成什么。

$$\begin{align}A(\omega_n^k)=&\sum_{i=0}^{n-1}a_i\omega_n^{ki} \nonumber\tag{3}\\=&\sum_{i=0}^{n/2-1}a_{2i}\omega_n^{2ki}+\sum^{n/2-1}_{i=0}a_{2i+1}\omega_n^{2ki+k}\nonumber\tag{4}\\=&\sum_{i=0}^{n/2-1}a_{2i}\omega_{n/2}^{ki}+\sum_{i=0}^{n/2-1}a_{2i+1}\omega_{n/2}^{ki}\omega_{n}^k\nonumber\tag{5}\\=&\sum_{i=0}^{n/2-1}a_{2i}\omega_{n/2}^{ki}+\omega_n\sum_{i=0}^{n/2-1}a_{2i+1}\omega_{n/2}^{ki}\nonumber\tag{6}\end{align}$$

我们来分别分析以下这几个神奇的步骤。

$(3)$步骤就是将$\omega_n^k$带入原来的$A$多项式。

$(4)$步骤就是将原多项式拆成两个部分，按奇偶分类。

$(5)$步骤用到了上面提到的性质$(2)$。

$(6)$步骤就是上面式子的后半部分提出公因数。

有了这个等式，我们就可以分治+递归解决DFT了。

算法步骤：

• 对当前的多项式（一个数组）系数进行奇偶分类；
• 递归算出偶数部分的数组的$ans_e$和奇数部分的数组的$ans_o$；
• 这个多项式的$ans=ans_e+\omega_nans_o$

但是这个的常数好像很大啊？能不能减少一点呢？

上面的性质$(1)$给了我们提示：

$$\omega_n^{n/2+k}=\omega_n^{n/2}\cdot \omega_n^{k}=-\omega_n^k$$

在算$k<\frac{n}{2}$时，可以顺便把$k\geq\frac{n}{2}$的情况也算出来。

常数减小了一半！但是还是很大啊！

递归版的程序一般比非递归版慢，为啥不用非递归版呢？

算法核心就是奇偶分类，分来分去最后分到了哪里？我们来研究研究。

显然，一个序列原来是$0,1,2,3,4,5,6,7$，最终变成$0,4,2,6,1,5,3,7$。

把它们的二进制列出来：

$$000,001,010,011,100,101,110,111\\000,100,010,110,001,101,011,111$$

其中，上面是位置，下面是这个位置对应的数。

把上面的数翻转，好像就是下面的数！

没错，只需要计算一下每个数的二进制翻转后的结果，就能得到一个数最终对应的位置，也就能实现非递归版了。

IDFT部分

回顾上面的DFT部分，仔细思考一下，它本质就是在求：

$$\begin{cases}a_0(\omega_n^0)^0+a_1(\omega_n^0)^1+\cdots+a_{n-1}(\omega_n^0)^{n-1}=A(\omega_n^0)\\a_0(\omega_n^1)^0+a_1(\omega_n^1)^1+\cdots+a_{n-1}(\omega_n^1)^{n-1}=A(\omega_n^1)\\\cdots\\a_0(\omega_n^{n-1})^0+a_1(\omega_n^{n-1})^1+\cdots+a_{n-1}(\omega_n^{n-1})^{n-1}=A(\omega_n^{n-1})\end{cases}$$

其中，给定了$a_0,a_1,\cdots, a_{n-1}$以及$\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}$，求$A(\omega_n^0),A(\omega_n^1),\cdots,A(\omega_n^{n-1})$的值。

用矩阵表示如下：

$$\begin{bmatrix}(\omega_n^0)^0&(\omega_n^0)^1&\cdots&(\omega_n^{0})^{n-1}\\(\omega_n^1)^0&(\omega_n^1)^1&\cdots&(\omega_n^1)^{n-1}\\\vdots&\vdots&\ddots&\vdots\\(\omega_n^{n-1})^0&(\omega_n^{n-1})^1&\cdots&(\omega_n^{n-1})^{n-1}\end{bmatrix}\begin{bmatrix}a_0\\a_1\\\vdots\\a_{n-1}\end{bmatrix}=\begin{bmatrix}A(\omega_n^0)\\A(\omega_n^1)\\\vdots\\A(\omega_n^{n-1})\end{bmatrix}\tag{7}$$

我们令：

$$V=\begin{bmatrix}(\omega_n^0)^0&(\omega_n^0)^1&\cdots&(\omega_n^{0})^{n-1}\\(\omega_n^1)^0&(\omega_n^1)^1&\cdots&(\omega_n^1)^{n-1}\\\vdots&\vdots&\ddots&\vdots\\(\omega_n^{n-1})^0&(\omega_n^{n-1})^1&\cdots&(\omega_n^{n-1})^{n-1}\end{bmatrix}$$

那么IDFT的本质就是求$V$矩阵的逆矩阵。

普通的矩阵求逆显然无法快速求出，这必须依靠人类智慧大力猜想逆矩阵。

人类智慧还真求出来了，考虑下面这个矩阵：

$$D=\begin{bmatrix}(\omega_n^{-0})^0&(\omega_n^{-0})^1&\cdots&(\omega_n^{-0})^{n-1}\\(\omega_n^{-1})^0&(\omega_n^{-1})^1&\cdots&(\omega_n^{-1})^{n-1}\\\vdots&\vdots&\ddots&\vdots\\(\omega_n^{-(n-1)})^0&(\omega_n^{-(n-1)})^1&\cdots&(\omega_n^{-(n-1)})^{n-1}\end{bmatrix}$$

那么我们令$E=D\cdot V$，则：

$$\begin{align}E_{i,j}=&\sum_{k=0}^{n-1}D_{i,k}V_{k,j}\nonumber\\=&\sum_{k=0}^{n-1}(\omega_n^{-i})^k(\omega_n^k)^j\nonumber\\=&\sum_{k=0}^{n-1}\omega_n^{k(j-i)}\nonumber\end{align}$$

显然：

$$E_{i,j}=\begin{cases}0(i\not= j)\\n(i=j)\end{cases}$$

因此

$$\frac{1}{n}D\cdot V=\frac{1}{n}E=I_n$$

$(7)$式两边同时左乘$\frac{1}{n}D$，可得

$$\begin{bmatrix}a_0\\a_1\\\vdots\\a_{n-1}\end{bmatrix}=\frac{1}{n}\begin{bmatrix}(\omega_n^{-0})^0&(\omega_n^{-0})^1&\cdots&(\omega_n^{-0})^{n-1}\\(\omega_n^{-1})^0&(\omega_n^{-1})^1&\cdots&(\omega_n^{-1})^{n-1}\\\vdots&\vdots&\ddots&\vdots\\(\omega_n^{-(n-1)})^0&(\omega_n^{-(n-1)})^1&\cdots&(\omega_n^{-(n-1)})^{n-1}\end{bmatrix}\begin{bmatrix}A(\omega_n^0)\\A(\omega_n^1)\\\vdots\\A(\omega_n^{n-1})\end{bmatrix}$$

这就相当于把DFT中$\omega_n^k$都换成$\omega_{n}^{-k}$。

IDFT过程中的小技巧

如果IDFT中逆矩阵使用的是$V$（使用的是DFT的过程），要得到IDFT的正确结果只需要执行一遍std::reverse(a+1,a+n)，这是很容易证明的。

NTT（快速数论变换）

FFT要求采用复数和实数运算，如果数很大很容易产生精度误差。如果是模意义下呢？

前置技能

FFT，初级数论内容，原根。

一点微小的变化？

考虑原根的性质。

性质$(1)$ 循环：$g_n^{n+x}=g_n^x \pmod{n}$

性质$(2)$ 折半：$g_n^x=g_{n/2}^{x/2}\pmod{m}$

性质$(3)$ $\sum_{i=0}^{n-1} g_n^i=0\pmod{m}$

可以发现原根的性质和单位根的性质差不多，因此可以用来做模意义下的FFT，就是NTT。

或者说，NTT就是把FFT的$\omega$替换成了$g$。

由于使用的是$g_i^{m-1}$，其中$m$为模数，$i$为$2^k$形式，因此模数是$x\cdot 2^k+1$的形式（NTT模数）。

常见的NTT模数：

998244353，原根是3

1004535809，原根也是3

FWT（快速沃尔什变换）

上面求的都是多项式卷积

$$F(n)=\sum_{i=0}^n a(i)b(n-i)$$
或者换种方式
$$F(n)=\sum_{i,j,i+j=n}a(i)b(j)$$
但是如果是下面的方式
$$F(n)=\sum_{i,j,i\circ j=n} a(i)b(j)$$
其中 $\circ$是种位运算呢？

依然考虑转化成点值表达式再相乘。类比FFT，考虑用一种变换$tf$和逆变换$utf$，只要$tf(A\times B)=tf(A)\times tf(B)$，那么就可以得到$A\times B=utf(tf(A)\times tf(B))$

下面我们分类讨论$\circ$的位运算种类及$tf,utf$的种类。

集合交卷积（and）

集合并卷积（or）

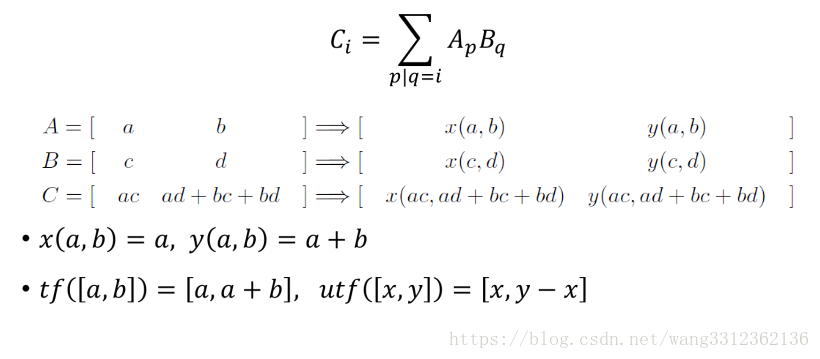
集合对称差卷积（xor）

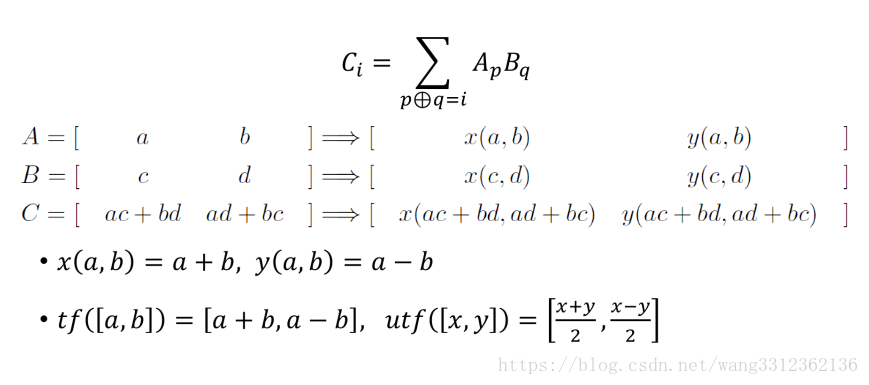
子集卷积

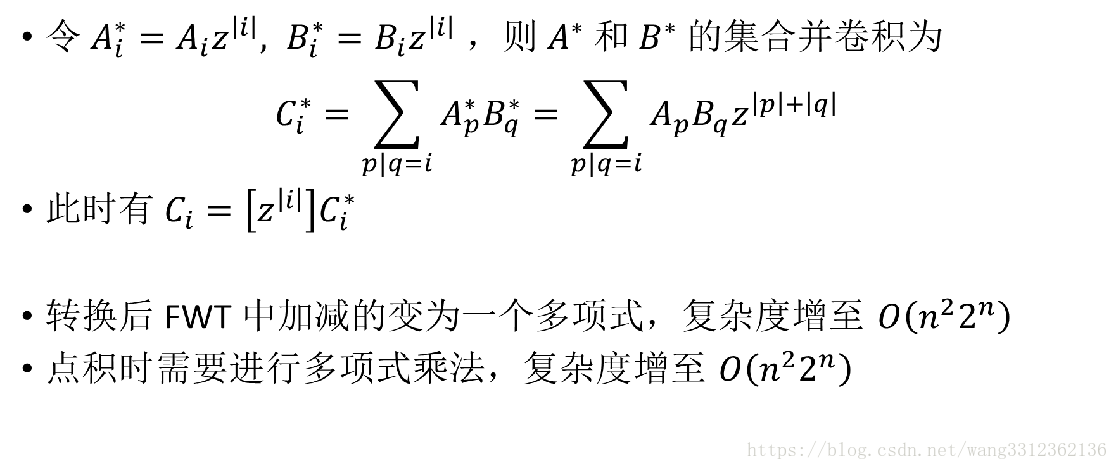
其他的方式

多项式求逆

前置技能

多项式乘法（FFT/NTT）

多项式的度

一个多项式的度就是这个多项式最高此项的次数，例如$4x^2+3x+1$的度为$2$。

多项式的逆元

现在有两个多项式$F,G$，如果

$$F\times G=1 \pmod{x^n}\tag{1}$$
并且 $G$的度小于等于 $F$的度，那么 $G$称为 $F$在模 $x^n$意义下的逆元。

怎么求？假设已经求出了$F$在模$x^{\lceil n/2\rceil}$下的逆元，为$G'$。

由定义得到

$$F\times G'=1 \pmod{x^{\lceil n/2\rceil}}\tag{2}$$

将$(1)$放到模$x^{\lceil n/2\rceil}$意义下

$$F\times G=1\pmod{x^{\lceil n/2\rceil}}\tag{3}$$
$(2)-(3)$得到
$$F\times G'-F\times G=0 \pmod{x^{\lceil n/2\rceil}}$$
两边平方，得到
$$F^2\times G^2-2\times F^2\times G'\times G+F^2\times G'^2=0\pmod{x^n}$$
同时除以 $F$并处理 $\bmod x^{n}$意义下为 $1$的项
$$G=2G'-FG'^2\pmod {x^n}$$
就是说，只要求出了模 $x^{\lceil n/2\rceil}$意义下的逆元，就可以求出模 $x^n$意义下的逆元。