统计学习方法（3）逻辑回归

1、从线性回归到逻辑回归（模型）

1.1 线性模型：

给定数据集 $\{(x_1, y_1), (x_2,y_2),...,(x_n,y_n)\}$，求参数 $\omega$满足如下回归模型：
$\hat y = \omega_0+\omega_1x_1+\omega_2x_2+...+\omega_nx_n$
线性回归模型的向量形式：
$\hat y = \omega^T·\bf x$
其中： $\theta^T$表示向量 $\theta$的转置（行向量变为了列向量）;
$\mathbf{x}$为每个样本中特征值的向量形式，包括 $x_{1}$，…， $x_{n}$，而且 $x_0$ =1。

模型求解：
基于最小二乘思想（方差最小）求解模型参数 $\omega$：
$\hat \omega^* = argmin{1\over m}\sum_{i=1}^m(\hat \omega^Tx^{(i)}-y{(i)})^2$
写成向量形式：
$\hat \omega^* = argmin(\hat\omega^T\bf x-y)^T(\hat\omega^T\bf x-y)$
另 $E_{\hat\omega}=(\hat\omega\bf x-y)^T(\hat\omega\bf x-y)$，对其求导：
${\partial E_{\hat\omega} \over \partial{\hat\omega}}=2X(X^T\omega-y)$
令导数为0，求正态方程得到：
$\hat \omega = (X^TX)^{-1}X^Ty$

注：当 $X^TX$列数大于行数（特征数大于样例数），为非满秩矩阵，需引入正则项。

若无法求解正态方程或数据量较大，可采用梯度下降法：
对任意一点 $x^{(i)}$的梯度：
${\partial E_{\hat\omega} \over \partial{\hat\omega}}=2x^{(i)}(\omega^T x^{(i)}-y)$
随机梯度下降：
$\omega_{j+1}:=\omega_j-\alpha\nabla f(x)=\omega_j+\alpha (y^{(i)}-\omega^T x^{(i)})x^{(i)}$

1.2 逻辑回归：

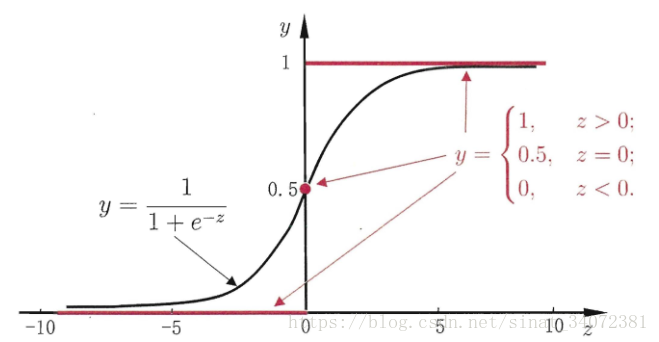
考虑二分类问题，由于线性回归输出值是 $\{-\infty,+\infty\}$，应选取合适的映射函数 $g^-(·)$，将模型输出映射为0/1值，这里想到单位阶跃函数可以做到，但是单位阶跃函数不连续，于是想到使用类似单位阶跃函数，又能单调可微的函数，所以可以使用对数几率函数，即sigmoid函数：
$y={1\over 1+e^{-z}}$

线性模型带入sigmoid函数，得到：
$y={1\over 1+e^{-({\bf \omega}^T{\bf x}+b)}}$
从而得到：
$log{y\over 1-y} = {\bf \omega}^T{\bf x}+b$
将y类后验概率估计 $p(y=1|x)$，则上式重写为：
$log{p(y=1|x)\over p(y=0|x)} = {\bf \omega}^T{\bf x}+b$
显然：
$p(y=1|x)={e^{({\bf \omega}^T{\bf x}+b)}\over 1+e^{({\bf \omega}^T{\bf x}+b)}}\\ p(y=0|x)={1\over 1+e^{({\bf \omega}^T{\bf x}+b)}}$
为了方便，将权重向量和输入向量加以扩充，于是得到逻辑回归模型：
$p(y=1|x)={e^{{\bf \omega}^T{\bf x}}\over 1+e^{{\bf \omega}^T{\bf x}}}\\ p(y=0|x)={1\over 1+e^{{\bf \omega}^T{\bf x}}}$
其中， $\omega=(\omega^{(1)},\omega^{(2)},... ,\omega^{(n)},b)^T，x=(x^{(1)},x^{(2)},... ,x^{(n)},1)^T$

2、策略

得到逻辑回归模型之后，考虑使用什么策略来学习模型。

2.1 极大似然估计

对于二分类，由于模型 $y_i\in \{0,1\}$服从0-1分布，设：
$P(Y=1|x) = \phi (z)，P(Y=0|x) = 1-\phi (z)$则概率分布可写为：
$p(y_i|x_i;\hat \omega) = \phi (z_i)^{y_i}(1-\phi (z_i))^{1-y_i}$
由于概率分布已知，根据观测数据，可采用极大似然估计法来估计参数 $\omega$和 $b$。

通过概率分布写出联合概率密度：
$L(\omega)=\prod_{i=1}^np(y^{(i)}|\theta, \omega) =\prod_{i=1}^n\phi(z^{(i)})^{y^{(i)}}(1-\phi(z^{(i)}))^{(1-y^{(i)})}$取对数可得：
$l(\omega)=\sum_{i=1}^nlnp(y^{(i)}|\theta, \omega) =\sum_{i=1}^ny^{(i)}ln[\phi(z^{(i)})]+(1-y^{(i)})ln[(1-\phi(z^{(i)}))]$
对 $L(\omega)$求极大值，可求出最有可能的 $\omega$。

2.2 损失函数

同其他统计学习方法一样，逻辑回归也可以使用损失函数来学习模型，逻辑回归使用的损失函数为对数损失函数：
$L(Y,P(Y|X))=-logP(Y|X)$
该模型的损失函数为：
$P(\phi(z), y|x; \omega)= \begin{cases} -ln\phi(z), & \text{if y=1} \\[2ex] -ln(1-\phi(z)), & \text{if y=0} \end{cases}$
由损失函数得到经验风险函数：
$J(\hat \omega)=-{1\over n}\sum_{i=1}^n(y_iln\phi(z^{(i)})+(1-y_i)ln(1-\phi(z^{(i)})))$

同极大似然法得到的对数似然函数比较，可以发现对数损失函数与极大似然估计的对数似然函数本质上是等价的，所以逻辑回归最小化对数损失函数求参数，实际上与采用极大化似然函数来求参数是一致的。

3、算法

由于对数似然函数是凸函数，故可采用数值优化算法如梯度下降法、拟牛顿法求其最优解。

以下采用梯度下降法：
令
$J(\theta) = -l(\omega)=-\sum_{i=1}^ny^{(i)}ln[\phi(z^{(i)})]+(1-y^{(i)})ln[(1-\phi(z^{(i)}))]$
$\frac{\partial J(\theta)}{\partial\theta_j} = -\sum_{i=1}^n[y^{(i)}{1\over \phi(z^{(i)})}-(1-y^{(i)}){1\over (1-\phi(z^{(i)}))}]\frac{\partial \phi(z^{(i)})}{\partial\theta_j}$
由于对于sigmoid函数：
$\phi'(z)=\phi(z)(1-\phi(z))$
$\frac{\partial (\omega^Tx+b)}{\partial \omega} = x$
故：
$=-\sum_{i=1}^n[y^{(i)}{1\over \phi(z^{(i)})}-(1-y^{(i)}){1\over (1-\phi(z^{(i)}))}]\phi(z^{(i)})(1-\phi(z^{(i)}))\frac{\partial z^{(i)}}{\partial\theta_j}$
$=-\sum_{i=1}^n[y^{(i)}(1-\phi(z^{(i)}))-(1-y^{(i)})\phi(z^{(i)})]x^{(i)}_j$
从而得到批量梯度下降：
$\theta_j:=\theta_j+\eta\sum_{i=1}^n(y^{(i)}-\phi(z^{(i)}))x^{(i)}_j$
随机梯度下降：
$\theta_j:=\theta_j+\eta(y^{(i)}-\phi(z^{(i)}))x^{(i)}_j，for\;i\;in\;range(n)$

4、实现

批量梯度下降：

    def train(self, X, y):
        """
        批量梯度下降：训练模型

        :param X: 输入集，n*m(n行m列)
        :param y: 标签集，1*m(1行m列)
        :return: 训练好的模型
        """
        n, m = np.shape(X)
        # X = (X, 1), w=(w;b)
        # w^T*x+b => w^T*X
        X = np.mat(np.concatenate((X, np.ones((n, 1))), axis=1))
        y = np.mat(y).T
        w = np.ones((m + 1, 1))

        alpha = self.alpha
        tol = self.tol
        records = []

        for i in range(self.max_iter):
            # 实际值与预测值之差
            error = y - 1.0 / (1 + np.exp(-X * w))
            # 误差变化记录
            records.append((error.T * error)[0, 0])
            if records[-1] <= tol:
                break
            # 负梯度方向更新参数
            w += alpha * X.T * error

        self.w = w[:-1]
        self.b = w[-1]

随机梯度下降：

    def train(self, X, y):
        """
        随机梯度下降

        :param X: 训练集
        :param y: 标签
        :return: w,b
        """
        n, m = np.shape(X)
        w = np.ones((m + 1, 1))

        alpha = self.alpha
        records = []

        for i in range(self.max_iter):
            row = random.randint(0, n - 1)
            x_i = np.mat(np.concatenate((X[row], np.ones(1))))
            y_i = y[row]
            error = y_i - 1.0 / (1 + np.exp(-np.matmul(x_i, w))[0, 0])
            records.append(error * error)

            w += alpha * error * x_i.T

        self.w = w[:-1]
        self.b = w[-1]