局部概率模型（Structured-CPDs）——揭示局部概率结构, 稀疏化网络表示

---

　　本博客中 PGM 系列笔记以 Stanford 教授 Daphne Koller 的公开课 Probabilistic Graphical Model 为主线，并参阅 Koller 著作及其 翻译版对笔记加以补充。博文的章节编号与课程视频编号一致。
　　博文持续更新（点击这里见系列笔记目录页），文中提到的资源以及更多见 PGM 资源分享和课程简介。

---

1 overview

　　本文讨论局部概率模（Structured-CPDs）。探索网络的局部结构（CPDs），理清条件概率分布中父节点变量间的关系，会发现更多好的独立性质，以此稀疏化网络的表示。同时对于连续变量，也避免了全概率分布表难以表达网络联合分布的问题。

1.1 从全局到局部

　　之前都在讨论独立性的全局性质的表示，使得一个高维联合分布能被分解为低维条件概率分布的乘积或因子的乘积$^{注*}$，而一直没有讨论这些因子的表示。
　　注*：即分解为形如 $P(X_1,...X_n)=\prod\limits^n_{i=1}P(X_i|Pa_{X_i}^{\mathcal G})$，单个因子 $P(X_i|Pa_{X_i}^{\mathcal G})$ 称为一个条件概率分布（CPD）或局部概率模型，是变量在其父节点上的 CPD。
　　本文将着眼于分布的局部结构（local sturcture），即这些因子。将详细讨论条件概率分布（CPD, Conditional Probability Distribution），描述一系列的表示并且根据我们可以利用的附加规则考虑它们的应用。由于 CPD 是全局联合分布概率的局部归一化，它比因子的约束更强，所以我们从 CPD 作为切入点进行讨论。

1.2 CPD 的表格表示及其缺陷

1.2.1 用表格表示 CPD

  完全由离散随机变量构成的空间上，形如 $P(X|Pa_{_{X}})$ 的 CPD 可以通过条件概率表格（CPT, Conditional Probability Table）来编码，避免了列出整个联合分布表（full table）。CPT 例如

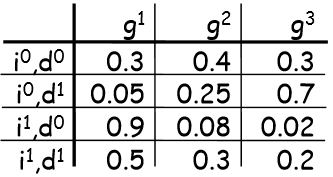
• 行：作为条件变量的赋值（assigment of appearance that give us）
• 列：未知变量的所有可能赋值列举（explicitly enumeratig all of the entries that correspond to G）

  这样的表格表示十分清晰，但有一定缺陷。比如

1.2.2 难以处理大规模问题

　　现实世界变量太多，变量间关系复杂即父节点太多（设 m 个），每个变量可能的取值很多（设 k 个）。仅一个变量的 CPD 其表格行数为 $O(k^m)$，成指数增长。

1.2.3 忽略 CPD 内在关系

　　可以由父节点 $Pa_{_{X}}$ 取值推出 $X$ 的条件分布 $P(X|Pa_{_{X}})$，但无法由给定 $X$ 反推其父节点的条件分布 $P(Pa_{_{X}}|X)$。

1.3 General CPD

  针对上述两条缺陷，我们希望 CPD 可以对每一个具体的 $x$ 和 $Pa_x$ 指定一个条件概率 $P(x|Pa_x)$，但是不必明确列出所有这样的值。我们应该把 CPD 看作是给定 $x$ 和 $Pa_x$，返回条件概率 $P(x|Pa_x)$ 的一个函数，而不是一个列出每个条件概率的表1。故 CPD 的一般形式如下

• CPD $P(X|y_1,...y_k)$ 明确了当 $Y$ 赋值为 $y_1,...y_k$ 时 $X$ 上的分布；
• 可以用任何函数来表示一个因子 $\phi(X,y_1,...y_k)$，但需要满足 $\sum_{X}\phi(X,y_1,...y_k)=1,\ for\ all\ y_1,...y_k.$

  注：这样 CPD 作为函数的含蓄表示，足以将每个定义明确的分布指定为一个贝叶斯网，这就是后文要讨论的。

1.4 CPD 的模型

• Deterministic CPDs（确定性 CPDs）
• Tree-Structured CPDs（树结构 CPDs）
• Logistic CPDs & generalizations（逻辑 CPDs & 一般化）
• Noisy OR/AND（含有 OR/AND 噪声）
• Linear Gaussians & generalizations（线性高斯 & 一般化）

1.5 确定性 CPD

• 确定性 CPD 定义

  当 $X$ 是其父节点 $Pa_{_{X}}$ 的确定性函数（deterministic function）时，即给定所有 $Pa_{_{X}}$ 时 $X$ 取值唯一。形式化表述为

$$P(x|Pa_x)=\begin{cases} 1, & x=f(Pa_{x})\\ 0, & other\ values \end{cases}$$ 　　含有确定性函数的 CPD 称作 确定性CPD（deterministic CPD）。

• 确定性 CPD 中包含更多独立性信息，而这些是无法从图的结构中直接读出来的。

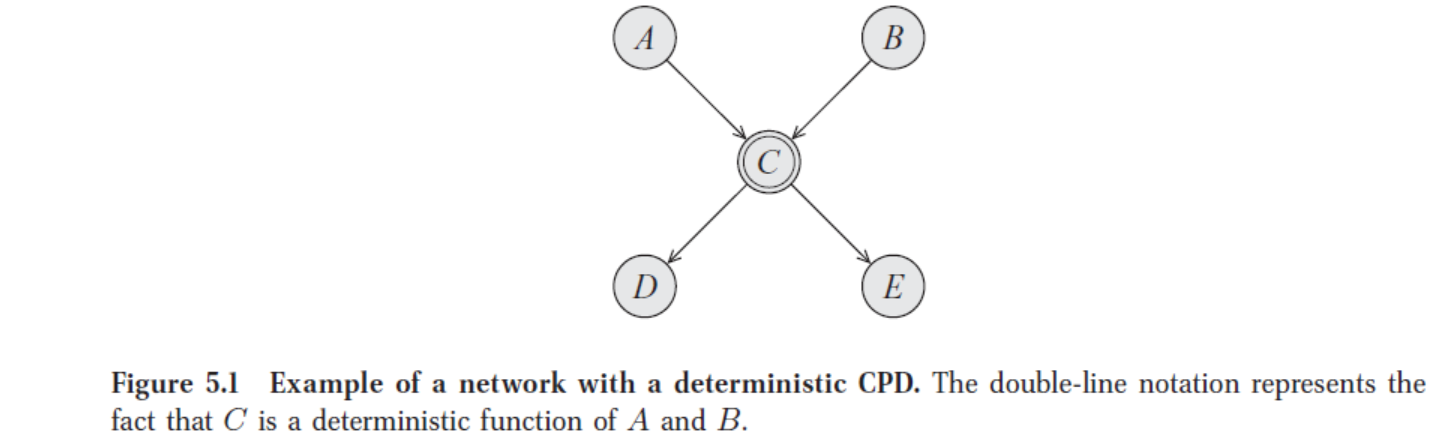
• 举例2：下图是一个包含确定性 CPD 的网络模型，这里是 A,B,C 均为二值变量，C 是 A, B 的确定性 OR，即 A, B 中至少一个为真则 C 为真。

　　由网络结构本身知 $(D\perp E|C)$，但结合确定性 CPD 之后推出 $(D\perp E|A,B)$ 也成立。

1.6 上下文特定的独立性

• 确定性变量**可以导出一种与标准的独立性概念

  进一步考察 1.5 的例子中 A,B,C 三者的结构关系：当 B 为真（取值为 1）时，C 和 A 独立。当 B 为假（取值为 0）时，C 和 A 相关。这不同于我们所熟知的独立（边缘独立）或条件独立。

　　事实上，确定性变量可以导出一种与标准的独立性概念（独立和条件独立）不同的独立性形式。这种独立性和特定变量的值有关：仅当特定变量取某个特定值时，才有独立关系成立。

• 上下文独立（contextually independent）定义

  $C$ 是变量集，可与 $X,Y,Z$ 相交，满足以下三条等价陈述时称 $X$ 与 $Y$ 在给定 $Z$ 和表示为 $(X\perp_c Y|Z)$ 的上下文 $c$ 时上下文独立。

$$\begin{array}\ P(X,Y|Z,c)=P(X|Z,c)P(Y|Z,c)\\ P(X,Y|Z,c)=P(X|Z,c)\\ P(X,Y|Z,c)=P(X|Z,c)\end{array}$$ 　　这种形式的断言称为 上下文特定的独立性（Context-Specific Independence）。在确定性依赖关系着以多种形式出现。

• 更多例子

　　注：Context-Specific Independence 也可能出现在条件概率表中，这仅当检查网络参数时，独立性才会显现出来。通过使 CPD 结构明确，这些独立性才可以用定性参数导出。

2 Tree-Structured CPDs

2.1 普通树形 CPD

2.1.2 结构理解

　　关于变量 $X$，可用普通树形 CPD（General Tree-Structured CPDs）表示其上的 CPD。树的结构如下：
　　 特别说明：为了与贝叶斯网中的术语“边”和“节点”区别，树形 CPD 内部的节点称作“树内节点”，树的边称作“弧”，树中“父节点”称作“树父节点”，叶节点称作“树叶节点”。以下“父节点”,“节点”，“边”都指的是原贝叶斯网中的相应结构。

• 树内节点 $Z_i$ 对应 $X$ 的父节点变量集，即 $Z_i\in Pa_{_{X}}$；
• 树叶节点对应不同的可能的（条件）分布，即 CPD；
• 通往每个树叶节点的路径，决定了使用这个 CPD 的上下文。

2.1.2 举例

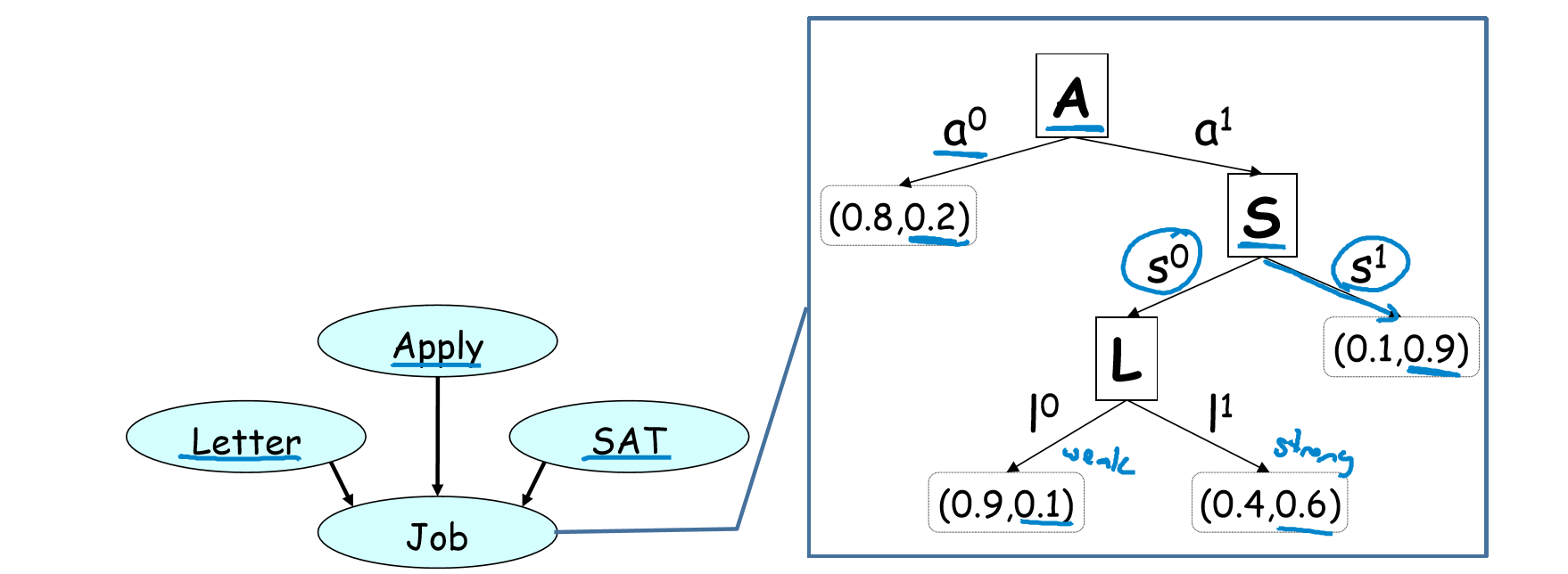
　　变量 Job 依赖于 Apply、SAT、Letter，即是否有工作取决于“是否主动申请”,“SAT 分数”,“是否有推荐信”三者。

• A=0 则 Job 有一定的 CPD $\spadesuit$
• A=1 则 Job 依赖于 SAT 分数高低：
  
  • S=1 则 Job 有一定的 CPD $\spadesuit$
  • S=0 则 Job 依赖于是否有 Letter：
    　· L=1 时 Job 有一定的 CPD $\spadesuit$
    　· L=0 时 Job 有一定的 CPD $\spadesuit$

   故该例子中有 4 个树叶节点 $\spadesuit$，即 4 种 CPD。但本来 3 个二值父节点 L, A, S 会导致 $2^3=8$ 种 CPDs。上例说明，当（此处借助树形 CPD）局部概率模型中独立性被挖掘地更清楚时，会使得 CPD 个数减少，即使分布有更稀疏的表示。

2.1.3 独立性

　　变量 $X$ 上的树中的一个树叶节点记作 CPD$_{_k}$，记通往该树叶节点的路径上为 $path_k$，对于 $Z_i\in Pa_x$：

• $Z_i\in path_k$ 是给定的证据变量，即为上下文；
• $Z_i\notin path_k$ 与 $X$ 在给定证据变量及其对于取值时上下文独立。

2.2 Multiplexer CPD

2.2.1 举例

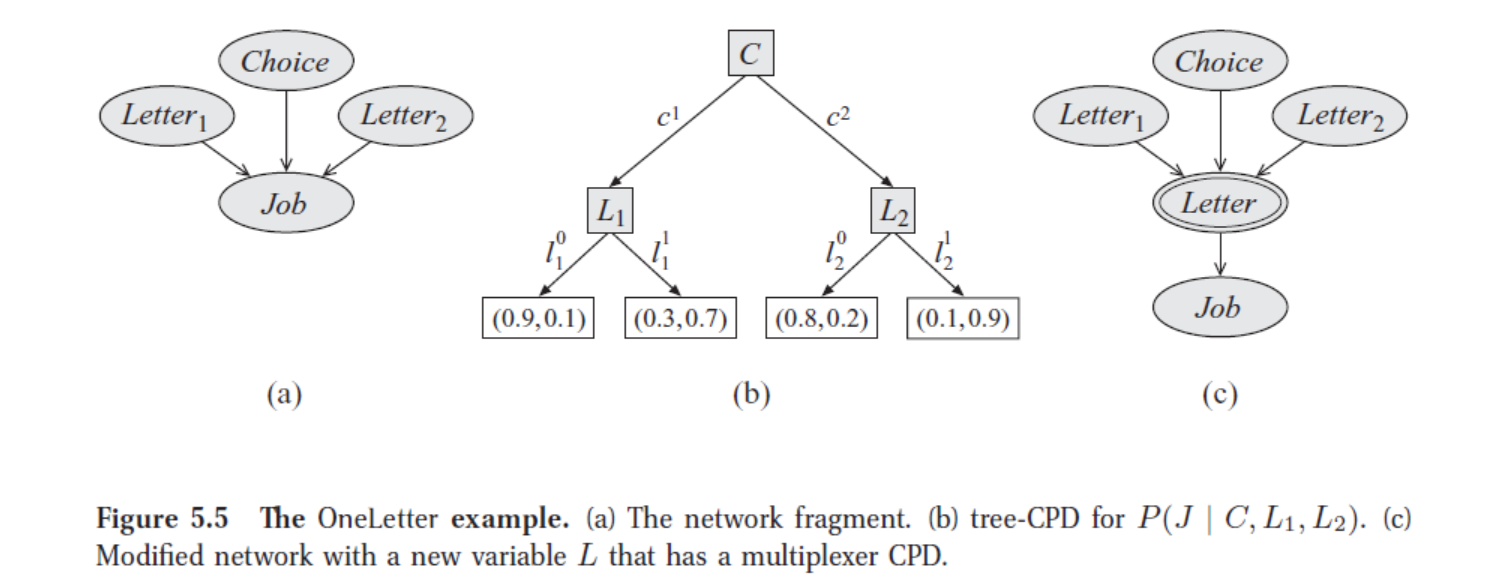
• 问题：Job 父节点为 Letter1, Letter2, Choice。Choice 选择投递哪一封推荐信3。
• 模型：

　　上图为该例的三种 CPD 模型：(a) 贝叶斯网下, (b) 选择树形 CPD, (c) 完善的 Multiplexer CPD（后文解释）。其中图 (b) 构建了一种带有选择性质的树形 CPD：
　　C=1 时 J 依赖于 L1；
　　C=2 时 J 依赖于 L2。

• 模型结构讨论：

  1）若只给定 J，L1 与 L2 不独立。因为通过 J 它们构成了V型交互因果（intercausal）迹；
  2）$(L_1\perp L_2|J,C)$，即条件独立性；
  3）$(L_1\perp_C L_2|J,c_1)$ 和 $(L_1\perp_C L_2|J,c_2)$，即上下文独立性；
　　4）可以把 C 看成是一个选择器（selector），决定 J 依赖于 L1 or L2。

2.2.2 一般化模型

　　 $X$ 的父节点集合为 $Pa_{_{X}}={Z_i}$， $y$ 是所有 $A$ 和 $Z_i$ 的确定性函数。

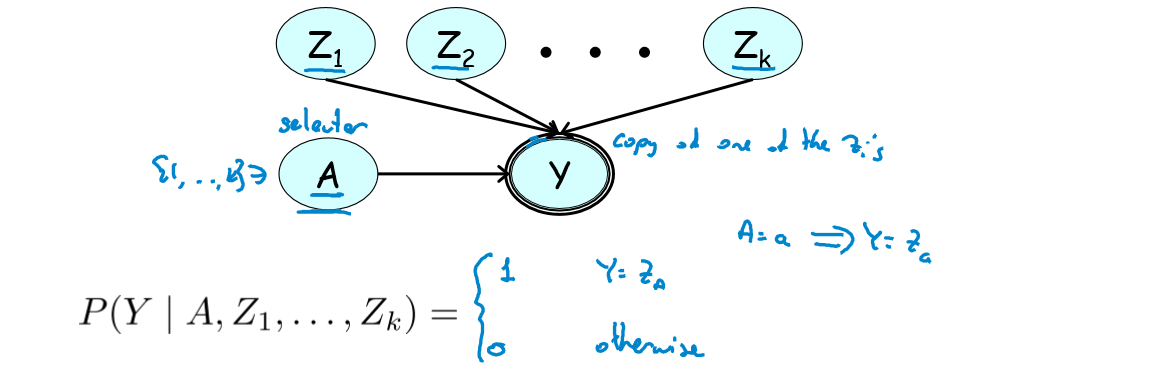
• 多路复用器（Multiplexer）：添加变量 $y$ 作为某个 $Z_i$ 的 copy；
• 选择器变量（selector variable）：$A$ 决定 $y$ copy 哪个 $Z_i$；

  此时，$X$ 由 $y$ 单一决定。这种 CPD 被称为一个多路复用器 CPD（Multiplexer CPD）。

2.3 树形 CPD 应用

　　举例：微软操作系统的错误检查（Microsoft Troubleshooter）模型。

2.4 树形 CPD 总结

　　已经看到，普通树形 CPD 通过上下文独立性减少了父节点变量，Multiplexer CPD 使得变量在不同情形下依赖于不同父节点。树形 CPD 有其特有的优势。

• 能挖掘一个变量的父节点之间的依赖关系（贝叶斯网不能）；
• 能有效捕捉 CPD 中的特定上下文独立性：
  
  • 从而有效减少模型变量个数
  • 进而减少最终的 CPDs 个数
• 应用广泛
  
  • Hardware configuration variables
  • Medical settings
  • Dependence on agent’s action
  • Perceptual ambiguity

3 Independence of causal influence

　　树形 CPD 通过简化 CPD 父节点变量，才使得模型得到极大简化，但当变量的每个父节点对该变量都有独立的影响时，上述模型便不适用。

　　对此讨论一类不同的局部概率模型：Noisy OR CPD 和广义高斯线性模型。

3.1 问题陈述

　　随机变量 $Y$ 所有父节点为 $X_i$，每个 $X_i$ 对 $Y$ 有直接$^{*1}$影响，且每个因果影响之间独立$^{*2}$。

　 　注：1）“直接”指 $X_i$ 与 $Y$ 之间有直接的因果影响（causal influence）。二值问题中指以某个的概率激活 $y$；
　　 　　2）“独立”指因果影响 $X_i-Y$ 与上下文无关。即 $X_i$是否影响 $Y$，影响有多大，都与 $X_j$ 无关；
　 　　　3）$X_i$ 两两之间也许有十分复杂的相互作用，但与前一条不矛盾。

3.2 Noisy OR CPD

　　在二值空间讨论 3.1 中的问题：一个结果是否发生依赖于其多个诱因是否发生，且原因之间相互独立。Noisy OR CPD　建立如下模型：

　　 思路：给诱因设立依赖于诱因的中间变量 $Z_i$，中间变量揭示了诱因发生的概率，结果依赖于中间变量的集成 $Z$。 4。
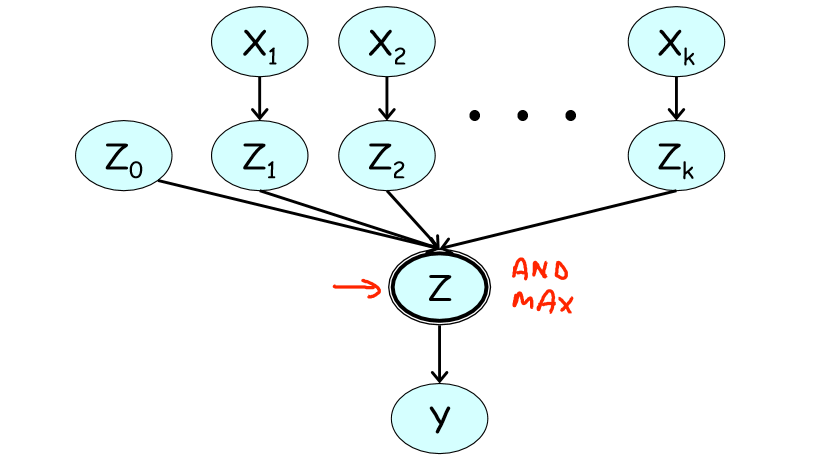
　　 模型： $Y$ 和 $X_i$ 均为二值随机变量，引入中间变量 $Z_i$， $y$ 是所有 $Z_i$ 的确定性 OR 函数。其中

• $Z_0$（noisy transmitter）: 噪声参数

  代表系统不确定性的，表示有某特定非 $X_i$ 的诱因导致结果 $y$ 发生的概率。它也是被结果依赖的二值变量，且没有父变量。

• $Z_i$（leak probability）

  表达 $X_i$ 单独成功激活 $Y$ 的概率（how good is $X_i$ at turning $Y$ on），由于 $y$ 是 $Z_i$ 的确定性 OR，所以如下赋值

$$P(Z=1|X_i)=\begin{cases} 0, & X_i=0\\ \lambda_i\in [0,1], & X_i=1 \end{cases}$$ 　　 预测：结果不发生的概率是所有诱因不发生的概率之积 $$P(Y=0|X_1,\ldots,X_k)=(1-\lambda_0)\prod_{i:X_i=1}(1-\lambda_i)$$ 　　取补即为结果发生的概率（compliment）则有 $$P(Y=1|X_1,\ldots,X_k)=1-P(Y=0|X_1,\ldots,X_k)$$ 　　 讨论：leak variable $Z_0$ 对预测结果的影响由下图可以体现

3.3 广义线性模型

　　思路：将发生的诱因对应的中间变量线性组合起来，然后利用 Sigmoid 或其他二值函数刻画结果是否发生。
　　模型：以 Sigmoid 函数为例，将其作为该广义线性模型的预测依据。类似 Noisy OR 中的 $Z_0$，这里引入 $\omega_0$ 作为偏好（bias）参数。

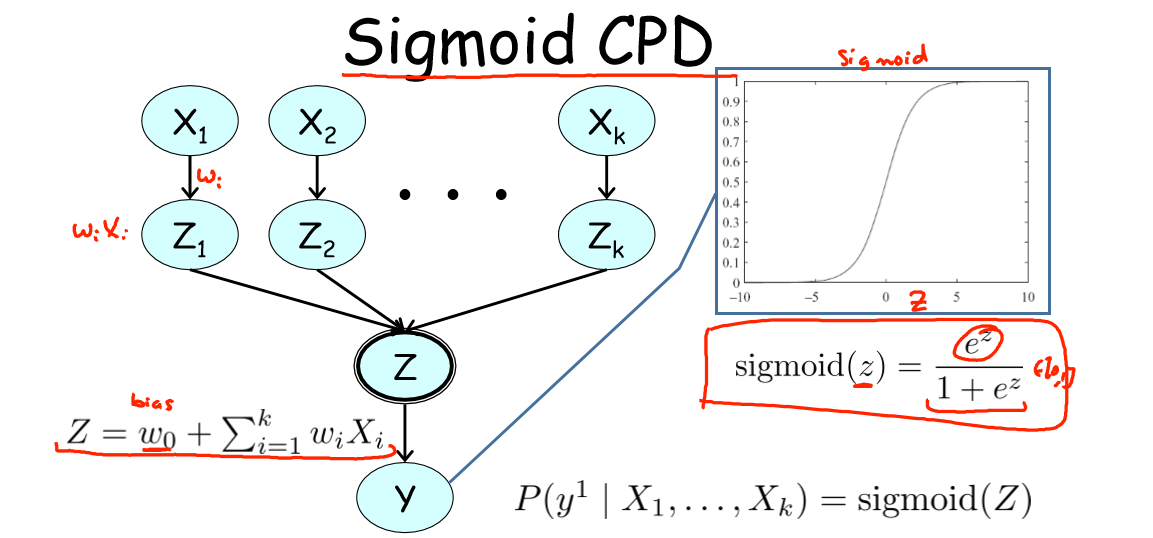
　　讨论：
　　1）偏好参数（bias）$\omega_0$ 大于 0 表示模型偏好预测结果为真，反之，则偏好预测结果为假；
　　2）当每个变量的权重越大，或发生的诱因个数越多，结果越有可能发生；
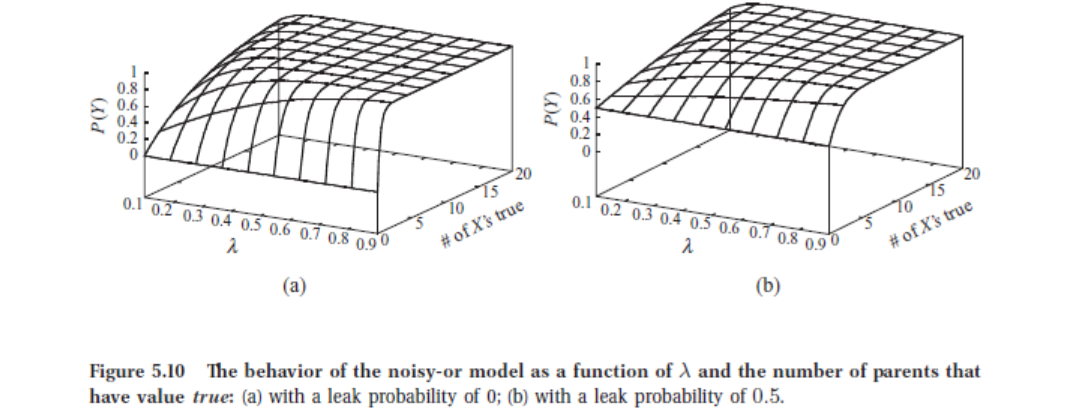
　　3）Behavior of Sigmoid CPD 如下5，看到（在左图基础上）增加诱因权重（右图）会使得 Sigmoid 函数变得陡峭。



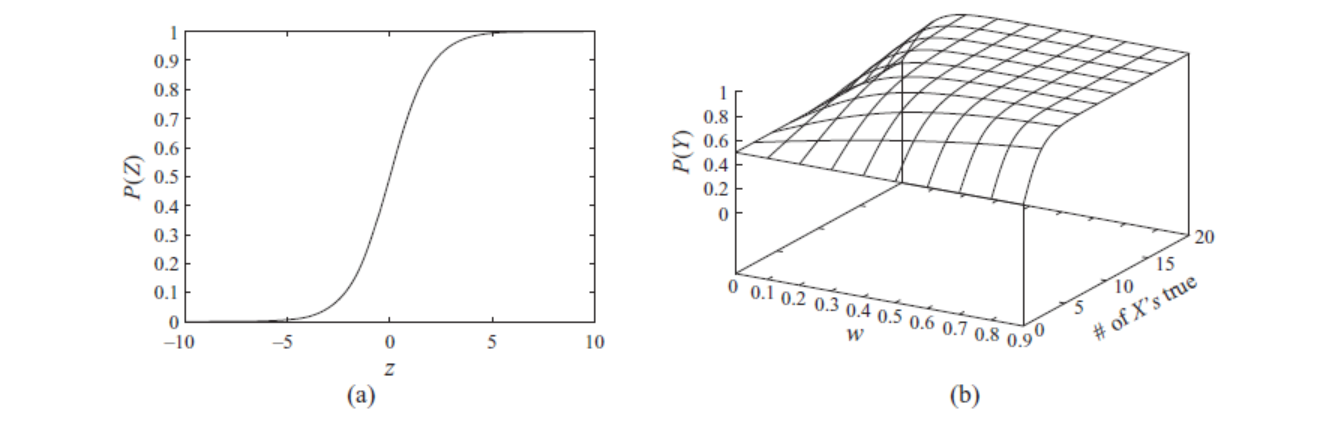
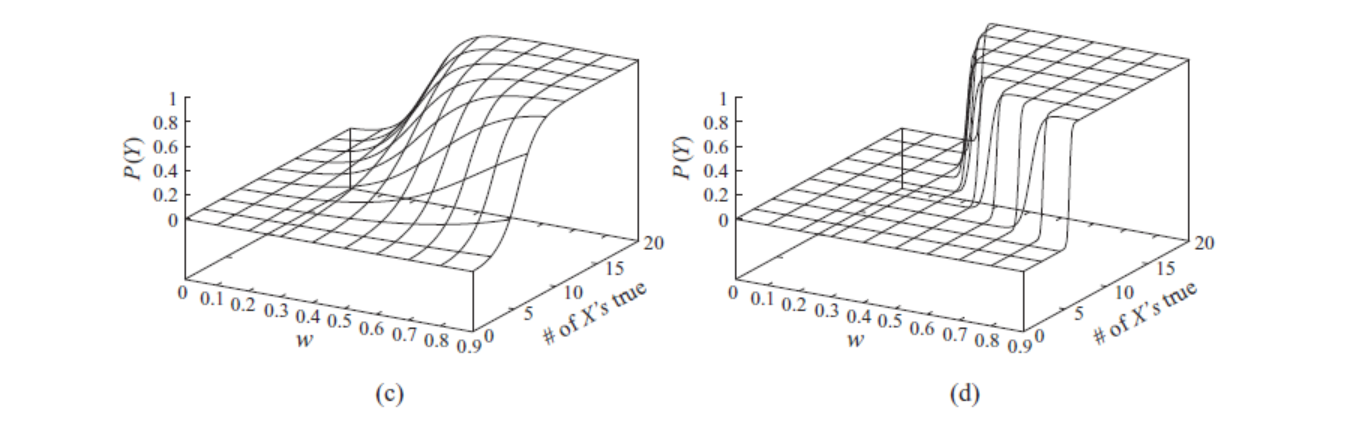
　 　注：参数 $\omega_i$ 对 Sigmoid CPD 的性态影响可根据其关于结果的对数几率（log-odds）影响，涉及“让步比”概念。参见 Koller 著作翻译版 Page 176.

3.4 因果影响的独立性

　　问题陈述：一类因果影响的问题中，结果依赖原因是否发生，原因之间相互独立。这种 CPD 形式满足因果影响的独立性。
　　解决思路：可以在每个原因之后加入一中间变量，它刻画原因是否发生；然后可以利用函数，对这些中间变量进行综合考虑，来影响最后的结果。

4 连续变量

　　CPDs 在概率图整体分布中挖掘了额外的局部结构，使整体分布可以表示地更稀疏。这在有连续变量（Continuous variables）的模型中更加至关重要，因为连续变量无法像离散变量那样列出联合分布概率表。

4.1 室温监控例子

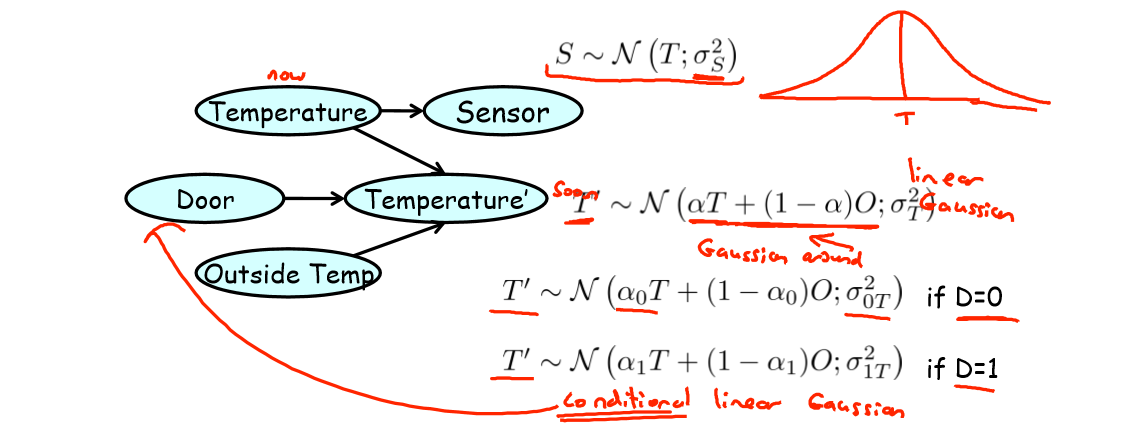
　　问题：下一时刻室内温度（Temperature’）取决于此时刻室内温度（Temperature），此时室外温度（Outside Temp），门的开关状态（Door）；传感器（Sensor）检测到的此时的室内温度记作 S。
　　分析：
　　1）问题即为已知 T’ 取决于 T, O 和 D，试图建立 T’ 的预测模型，模型变量为 S, O 和 D；
　　2）由于系统的 stochasticity，所以 S 是 T 加入了 noise 之后的结果，可以假设 S 服从正太分布。
　　模型：由于 S 中的 noise，最终的模型表示为以 O 和 T 的线性组合结果为均值（mean）的高斯分布（正太分布），其方差与门的开关状态 D 有关。

4.2 高斯线性模型

　　假设一个变量（子变量）依赖于一些连续变量（父变量），且子变量服从均值为父变量的线性组合，方差为常数的高斯分布。则称该模型为高斯线性模型。

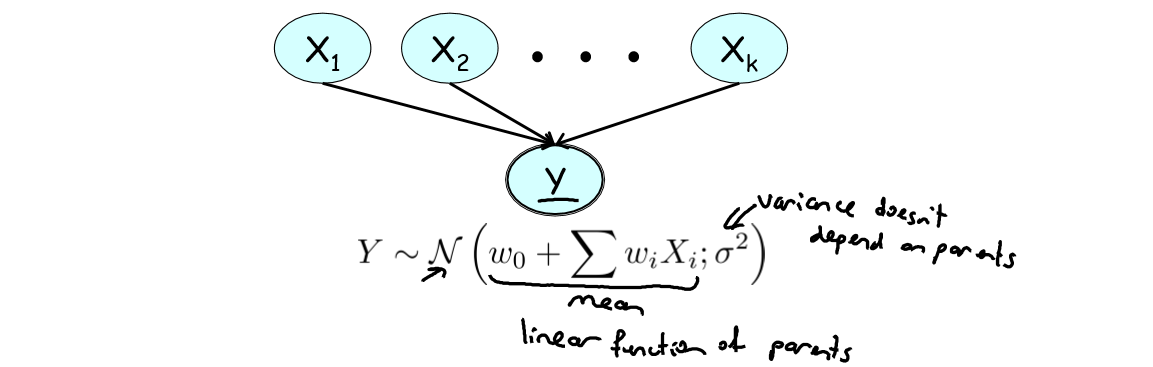
　　上图清晰表达了线性高斯（Linear Gaussian）模型结构，这里补充说明：
　　1 )“高斯”是由于连续随机变量 $y$ 的分布服从高斯分布；
　　2 )“线性”是由于该高斯分布的均值是 $y$ 的父节点的线性组合，且此模型中 $y$ 的高斯分布的方差是一个固定的模型参数，不取决于父节点变量，故整个模型是一个线性模型。

4.3 条件线性高斯模型

　　在满足线性高斯模型假设的前提下，如果子变量还依赖于一些离散随机变量，且这些离散随机变量影响原高斯线性模型中的所有参数（parameters are conditioned on the discrete variables），则称该模型为条件高斯分布（Conditional Linear Gaussian）。
　　可以看到，这时分布法方差与父节点以外的某因素相关，这正是线性高斯模型和条件线性高斯模型的区别。

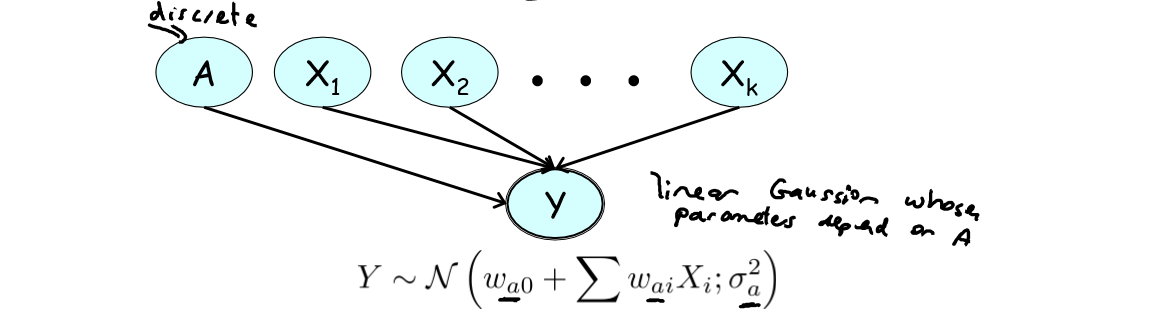
　　条件线性高斯模型引入离散变量 A 来确定模型参数，比如温度监控例子中的 Door 变量：
　　D=1，门是开的，室外温度 O 的参数将会相应的比较大；
　　D=0，门是关的，室外温度 O 的参数将会相应的比较校；
　　
　　1）由于所有模型参数都和 A 有关，故 $y$ 的高斯分布的方差也取决于 A 。故 $y$ 的分布不是其父节点的线性函数，此时不是 Linear Gaussian；
　　2）但一旦 A 的值取定为 $a$，模型的所有参数 $\omega_{a_i}$ 和 $\sigma_a$ 也相应确定。这时模型退化为 Linear Gaussian。
　　
　　Conditional Linear Gaussian 当条件给定后，会退化为 Linear Gaussian.

4.3 机器人定位模型

　　问题：非线性高斯分布在机器人定位（Robot Localization）中的应用，希望借助传感器预测机器人与某给定障碍物间的距离。
　　分析：问题含有“位置”这个连续变量，由于多种不确定因素，故采用非线性高斯模型做结果预测。
　　模型：父变量是实际距离，子变量是探测器给出的观测距离。预测距离的结果是均值为机器人实际距离的近似高斯分布，其方差取决于传感器（sensing modality）精度。

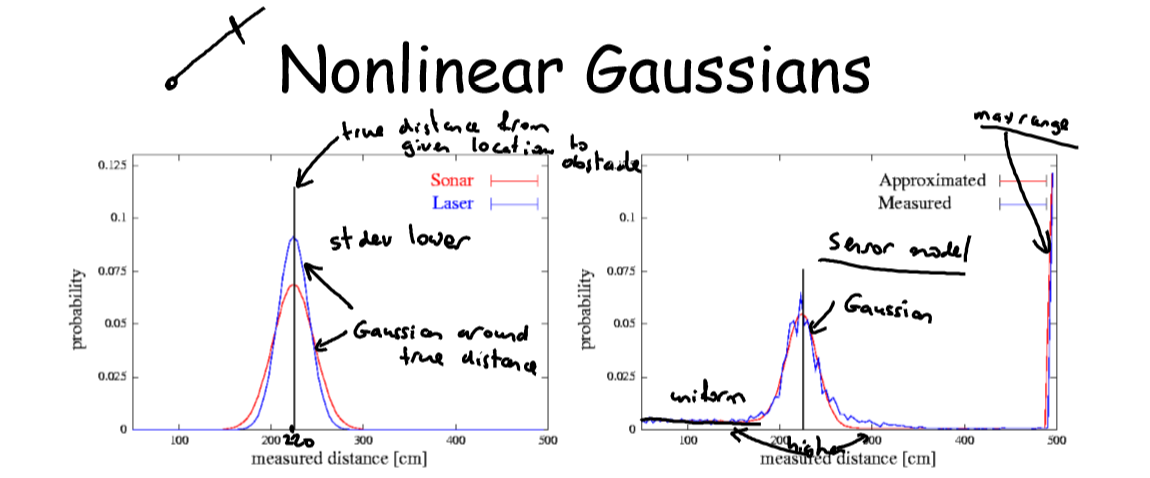
　　1）左图是理想状态下的预测模型：预测距离是均值为实际距离，方差取决于传感器精度的高斯分布。可以看到 Laser 比 Sonar 精度高，分布方差更小。

　　2）右图式应用中真实的预测模型：一个近似的高斯分布模型。分布图像有如下特征
　　
　　a）有两个峰值（peak），较低峰值（偏左）为实际距离，较高峰值（偏右）为传感器最大观测距离（max range reading）。这是由于传感器观测距离有限，所以超过这个距离的障碍物都被观测为该距离；
　　b）实际距离左侧图像比右侧陡峭，即障碍物前的概率密度（probability mass）大于其后的。这是由于机器人与障碍物之间存在随机外因，比如有人从机器人和障碍物间经过，会返回短暂的欺骗信号（transient-spurious returen）。这使得观测结果更倾向于观测到更小的距离。

  为什么是“近似”高斯分布？如 a), b) 所解释，真实预测模型事实上是三个信号的综合（aggregation）：

• 在给定探测方向的传感器模型
• 传感器最大观测距离
• 障碍物前短暂欺骗信号的高斯分布

4.3 机器人移动模型

　　问题：非线性高斯模型在机器人移动模型（Robot Motion Model）中的应用，希望机器人在自主移动过程中预测自己的位置。
　　分析：比定位模型中新增连续变量“前进方向”，机器人认为自己前进的方向和它实际前进的方向之间有一个服从高斯分布的误差。
　　模型：在上述模型的基础上引入一个新变量表示其移动轨迹与观测器的夹角。

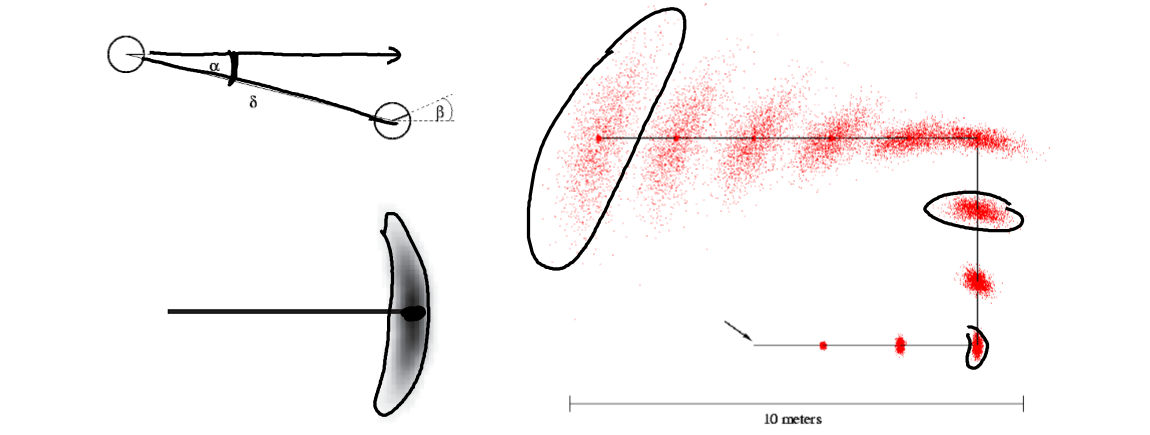
　　结果：如图所示，可以得到预测结果是的一系列中心浓密两边稀疏的香蕉型分布。并且随着运动，误差不断积累，香蕉型分布区域越来越大。