简化一下题意,我们先看成一副强连通的图,这时候应该是最简单了,去点任意点都是其他的乘积。那再加强一点难度,改为两个强连通图连接的非强连通图呢?那应该就是找出关键的那个点,并求出两边的乘积。但是一个一个去找是不可能的。
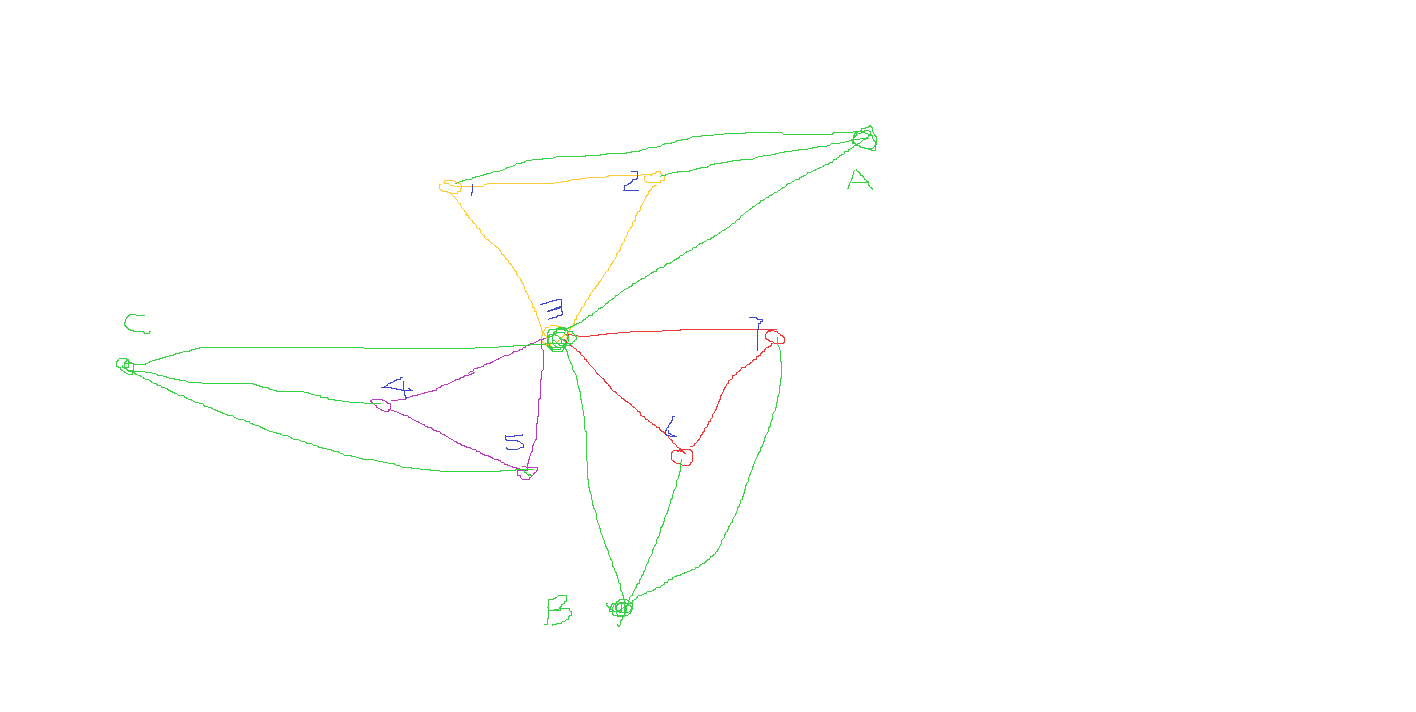
假设如图中的非绿色线是题目给的图。然后我们根据强连通分量去新建一副如图中绿色线条的图,那么这时候我们就把原图转化为以可树了。。对于每一个点我们求的是该点以及以下的乘积。然后我们从A出发这时候我们发现A点的值刚好就是整幅图的乘积。这时候如果我们需要求删除3这个点的得到的结果应该就是整一副图去除以3点及一下的乘积得到1,2的乘积,再加上3点的子树的乘积和也就是4、5 和 6、7的乘积和。
这道题目的难点就是转化建图的那一个步骤,应该说是最核心的部分。
#include<bits/stdc++.h> #define LL long long using namespace std; const int maxn = 1e5 + 7; const LL mod = 1e9 + 7; LL n, w[maxn], vis[maxn << 1], sum[maxn << 1], pro[maxn << 1]; struct oldEdge{ int v, next; bool flag; }; int oldHead[maxn], ocnt; oldEdge oedge[maxn << 2]; void addOldEdge(int u, int v){ oedge[ocnt].v = v; oedge[ocnt].flag = false; oedge[ocnt].next = oldHead[u]; oldHead[u] = ocnt ++; } struct newEdge{ int v, next; }; int newHead[maxn << 1], ncnt; newEdge nedge[maxn << 5]; void addNewEdge(int u, int v){ nedge[ncnt].v = v; nedge[ncnt].next = newHead[u]; newHead[u] = ncnt ++; } int dfn[maxn], low[maxn], root[maxn], rn, cnt; stack<int>sta; void tarjan(int u, int fa){ dfn[u] = low[u] = ++cnt; for(int i = oldHead[u]; i != -1; i = oedge[i].next){ if(oedge[i].flag) continue; oedge[i].flag = oedge[i ^ 1].flag = true; sta.push(i); int v = oedge[i].v; if(dfn[v]){ low[u] = min(low[u], dfn[v]); continue; } tarjan(v, fa); low[u] = min(low[u], low[v]); if(low[v] >= dfn[u]){ rn ++; int ek; do{ ek = sta.top();sta.pop(); root[oedge[ek].v] = root[oedge[ek ^ 1].v] = fa; addNewEdge(rn, oedge[ek].v); addNewEdge(oedge[ek].v, rn); addNewEdge(rn, oedge[ek ^ 1].v); addNewEdge(oedge[ek ^ 1].v, rn); }while(oedge[ek ^ 1].v != u); } } } void dfs(int u){ vis[u] = true; sum[u] = 0; pro[u] = (u <= n) ? w[u] : 1; for(int i = newHead[u]; i != -1; i = nedge[i].next){ int v = nedge[i].v; if(vis[v]) continue; dfs(v); if(u <= n) sum[u] = (sum[u] + pro[v]) % mod; pro[u] = pro[u] * pro[v] % mod; } } LL inv(LL a){ int p = mod - 2; LL ret = 1; while(p){ if(p & 1)ret = ret * a % mod; a = a * a % mod; p >>= 1; } return ret; } void init(){ memset(root, 0, sizeof(root)); memset(newHead, -1, sizeof(newHead)); memset(oldHead, -1, sizeof(oldHead)); memset(dfn, 0, sizeof(dfn)); memset(vis, false, sizeof(vis)); ncnt = ocnt = cnt = 0; } int main(){ int T, m, a, b;scanf("%d",&T); while(T --){ scanf("%lld%d",&n,&m); init();rn = n; for(int i = 1; i <= n; i ++)scanf("%lld",&w[i]); for(int i = 0; i < m; i ++){ scanf("%d%d",&a,&b); addOldEdge(a,b); addOldEdge(b,a); } for(int i = 1; i <= n; i ++) if(!dfn[i])tarjan(i, rn + 1); LL tot = 0; for(int i = 1; i <= n; i ++){ if(vis[i]) continue; if(root[i]){ dfs(root[i]); tot = (tot + pro[root[i]]) %mod; }else tot = (tot + w[i]) % mod; } LL ans = 0; for(int i = 1; i <= n; i ++){ if(root[i]){ LL temp = ((tot - pro[root[i]] + pro[root[i]] * inv(pro[i]) + sum[i]) % mod + mod) * i % mod; ans = (ans + temp) % mod; } else ans = ((ans + (tot - w[i]) * i) % mod + mod) % mod; } printf("%lld\n",ans); } return 0; }