【缄*默】 #图论# 图论知识点全面总结

一. 图的储存结构

【1.1 邻接矩阵】

图的邻接矩阵存储方式是用两个数组来表示图。

一个一维数组存储顶点信息，一个二维数组（邻接矩阵）存储边的信息。

设图G有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

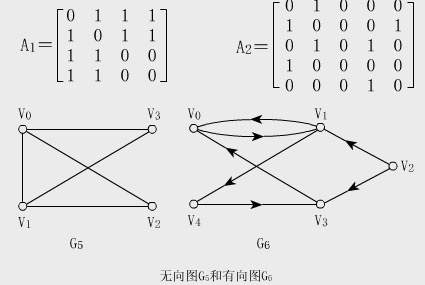
看一个实例，下图左就是一个无向图。

从上面可以看出，无向图的边数组是一个对称矩阵。

所谓对称矩阵就是n阶矩阵的元满足aij = aji。

从这个矩阵中，很容易知道图中的信息：
（1）判断任意两顶点是否有边连接；
（2）某个顶点的度就是顶点vi在邻接矩阵中第i行或（第i列）的元素之和；
（3）顶点vi的所有邻接点就是矩阵中第i行元素arc[i][j]为1的点；

而有向图讲究入度和出度，vi入度为1，是第i列各数之和；vi出度为2，是第i行各数之和。

若图G是网图，有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

其中，w[i][j]表示(vi,vj)边上的权值。

//【图的储存---邻接矩阵】O(n^2)

#define MaxN 20
int G[MaxN][MaxN];

void add_sqr(){
    int v1,v2,w,n,m;
    scanf("%d%d",&n,&m);
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++) G[i][j]=0;
    for(int i=0;i<m;i++){
        scanf("%d%d%d",&u,&v,&w);
        G[u][v]=w; G[v][u]=w; //无向图，双向边
    }
}

从代码中可以得到，时间复杂度为O(n + n^2 + e)，

其中对邻接矩阵Grc的初始化耗费了O(n^2)的时间。（部分引用自这里）

图的邻接矩阵

【1.2 邻接表】

对于边数相对顶点较少的图，邻接矩阵极大浪费了存储空间。

因此，有一种数组与链表相结合的存储方法称为邻接表。

邻接表的处理方法是这样的：

（1）顶点用一维数组或单链表来存储，不过数组更便捷。

（2）图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点个数不定，

所以要用单链表存储，这种链表在无向图称为顶点vi的边表。

在有向图中则被称为顶点vi作为弧尾的出边表。

例如，下图就是一个无向图的邻接表的结构。

从图中可以看出，顶点表的各个结点由data和firstedge两个域表示：

data是数据域，存储顶点的信息。（一般是初始出边）
firstedge是指针域，指向边表的第一个结点，即此顶点的第一个邻接点。

边表结点由adjvex和next两个域组成：

adjvex是邻接点域，存储某顶点的邻接点在顶点表中的下标。
next则存储指向边表中下一个结点的指针。

对于带权值的网图，可以在边表结点定义中再增加一个weight的数据域。

对于邻接表结构，图的建立代码如下。

//【图的存储---链式前向星】O(m)

#define MaxN 20

struct edge{
    int ver,nextt; //边的终点 和 顶点链表中下一条边的存储位置
}Edge[MaxN*MaxN]; //顶点数^2（也可以开maxm）

int head[MaxN]; //head[i]表示以i为起点的第一条边的存储位置
//head数组一般初始化为-1，注意存储顺序与输入顺序相反
int tot;
int N,M;//节点个数以及边的条数

void clears(){ tot=0; memset(head,-1,sizeof(head)); }
 
void add(int x ,int y){
    Edge[tot].ver=y; Edge[tot].nextt=head[x];
    head[x]=tot; tot++; //从0号开始标记节点
}
 
int main(){
    clears(); cin>>N>>M; int x,y;
    for(int i=1;i<=M;i++){
        cin>>x>>y; add(x,y); //有向图，只有一个方向
    }
    for(int i=1;i<=N;i++){
        ......
    }
    ......
    return 0;
}

建图的时间复杂度为O(m)，查询的复杂度也相同。

二. 图的遍历

图的遍历是指从图中的任一顶点出发，对图中的所有顶点恰好访问一次。

求解图的连通性问题，拓扑排序，求关键路径等问题都是建立在遍历算法的基础之上。

① 没有确定的首结点，图中任意一个顶点都可作为第一个被访问的结点。

② 在非连通图中，从一个顶点出发，只能够访问它所在的连通分量上的所有顶点，

因此，还需考虑如何选取下一个出发点以访问图中其余的连通分量。

③ 如果有环存在，那么一个顶点被访问之后，有可能沿回路又回到该顶点。

④ 一个顶点可以和其它多个顶点相连，存在如何选取下一个要访问的顶点的问题。

图的遍历通常有深度优先搜索和广度优先搜索两种方式，二者对无向图和有向图都适用。

【2.1 深度优先搜索】

深度优先搜索遍历类似于树的先根遍历，是树的先根遍历的推广。

初始状态是图中所有顶点未曾被访问，可从图中某个顶点v出发，访问此顶点，

依次从v 的未被访问的邻接点出发，直至图中所有和v 有路径相通的顶点都被访问到。

若此时图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，

重复上述过程，直至图中所有顶点都被访问到为止。

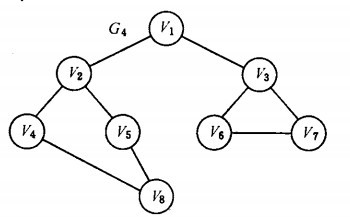
以如下图的无向图为例，进行图的深度优先搜索：

搜索过程：

假设从顶点v1 出发进行搜索，在访问了顶点v1 之后，选择邻接点v2。
因为v2 未曾访问，则从v2 出发进行搜索。接着从v4 、v8 、v5 出发进行搜索。
在访问了v5 之后，由于v5 的邻接点都已被访问，则搜索回到v8。
由于同样的理由，搜索继续回到v4，v2 直至v1。
此时由于v1 的另一个邻接点未被访问，则搜索又从v1 到v3...

再继续进行下去。得到的顶点访问序列为：

为了标记是否已被访问，要设标志数组vis[0~n-1] ，其初值为FALSE。

邻接表储存 >

#define N 5 
using namespace std; 
int maps[N][N] = { { 0, 1, 1, 0, 0 }, 
                   { 0, 0, 1, 0, 1 },
                   { 0, 0, 1, 0, 0 }, 
                   { 1, 1, 0, 0, 1 }, 
                   { 0, 0, 1, 0, 0 } }; 

int vis[N + 1] = { 0 };

dfs递归实现 >

//递归实现

void DFS(int start){ 
    vis[start] = 1; 
    for(int i=0;i<N;i++)
        if(!vis[i]&&maps[start][i]==1) DFS(i);  
    cout<<start+1<<" "; 
} 

int main(){
    for(int i=0;i<N;i++){ 
        if(vis[i]==1) continue; DFS(i);
    } return 0; 
}

【栈】非递归实现 >

//优化：非递归实现【栈】

void DFS(int start){
    stack<int> s;  s.push(start); 
    bool is_push=false; vis[start]=1;
    while(!s.empty()){
        is_push=false; int v=s.top(); 
        for(int i=0;i<N;i++) 
            if(maps[v][i]==1&&!vis[i]){ 
                vis[i]=1; s.push(i); is_push=true; break; 
            }
        if(!is_push){ cout<<v<<" "; s.pop(); } 
    } 
}

int main(){ 
    for(int i=0;i<N;i++){ 
        if(vis[i]==1) continue; DFS(i); 
    } return 0; 
}

【2.2 广度优先搜索】

广度优先搜索遍历类似于树的按层次遍历的过程。

从图中某顶点v 出发，访问v 之后依次访问v 的各个未曾访问过和邻接点，

然后分别从这些邻接点出发依次访问它们的邻接点，

并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问，

直至图中所有已被访问的顶点的邻接点都被访问到。

若此时图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，

重复上述过程，直至图中所有顶点都被访问到为止。

换句话说，广度优先搜索遍历图的过程中以v 为起始点，

由近至远，依次访问和v 有路径相通且路径长度为1,2,…的顶点。

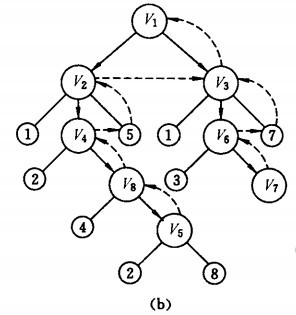
下图中无向图进行广度优先搜索遍历：

广度搜索过程：

首先访问v1 和v1 的邻接点v2 和v3，
然后依次访问v2 的邻接点v4 和v5 及v3 的邻接点v6 和v7，
最后访问v4 的邻接点v8。

顶点的邻接点均已被访问，完成了图的遍历。得到的顶点访问序列为：

v1→v2 →v3 →v4→ v5→ v6→ v7 →v8

和深度优先搜索类似，在遍历的过程中也需要一个访问标志数组。

并且，为了顺次访问顶点，需设队列存储已被访问的路径长度为1、2、… 的顶点。

 //【广搜】+【队列】

void BFS(int start){
    queue<int> Q; Q.push(start); 
    vis[start]=1; //标记已访问
    while(!Q.empty()){ 
        int front=Q.front(); 
        cout<<front+1<<" "; Q.pop(); //输出广搜的入队（出队）顺序
        for(int i=0;i<N;i++)
            if(!vis[i]&&maps[front][i]==1) vis[i]=1, Q.push(i); 
    }
} 

int main() { 
    for(int i=0;i<N;i++){ 
        if(vis[i]==1) continue; BFS(i); 
    } return 0; 
}

三. 图的连通性

四. 最短路问题

【4.1 拓扑排序】

概念解析

拓扑排序：将一个有向无环图进行排序，进而得到一个有序的线性序列。

例如，一个项目包括A、B、C、D四个子部分来完成，并且A依赖于B和D，C依赖于D。

现在要制定一个计划，写出A、B、C、D的执行顺序。利用拓扑排序，用来确定事物发生的顺序。

在拓扑排序中，如果存在一条从顶点A到顶点B的路径，那么在排序结果中B出现在A的后面。

基本步骤

1. 构造一个队列 Q 和拓扑排序的结果队列 T；

2. 把所有没有依赖顶点的节点放入 Q；

3. 当 Q 还有顶点的时候，执行下面步骤：

3.1 从 Q 中取出点 n (将 n 从 Q 中删掉)，并放入 T (将 n 加入到结果集中)；

3.2 对 n 每一个邻接点 m ( n 是起点， m 是终点)；

3.2.1 去掉边 < n , m >；

3.2.2 如果 m 没有依赖顶点，则把 m 放入 Q；

注：顶点A没有依赖顶点，是指不存在以A为终点的边。

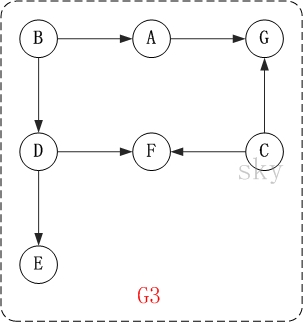
以上图为例，来对拓扑排序进行演示。

由图示过程，可得顺序为：B -> C -> A -> D -> E -> F -> G 。

代码说明

五. 最小生成树

六. 树的直径与LCA

七. 基环树

八. 负环与差分约束

【8.1 负环】

若图中存在一个环，各边的权值之和是负数，则称这个环为负环。

考虑求单源最短路问题的各种算法的使用条件：

	能否处理负权边	时间复杂度
Dijkstra	不能，当前最小不一定能实现全局最小。	$O\left ( n^{2} \right )$
Heap_Dijkstra	不能，等价于选最小的 dist [ x ] 。	$O\left ( m log n \right )$
Bellman_Ford	能，最短路径包含的边数<n， n-1轮以后一定能实现所有的边值收敛。	$O\left ( nm \right )$
SPFA	能，负环只会是增加出入队次数。	$O\left ( km\cdots nm \right )$

总结：判负环的基本方法

1.【Bellman_Ford】若经过n轮迭代，算法仍未结束，

（即仍有能产生更新的边）则图中存在负环。

2.【SPFA】用 cnt [ x ] 表示从1到x的最短路径包含的边数。

在更新 dist [ y ] = dist [ x ] + z 时，同时更新 cnt [ y ] = cnt [ x ] + 1 。

若发现 cnt [ y ] >= n，则图中有负环。

3.【SPFA】记录每个点入队的次数，某点达到n次时说明有负环。

4.【设置上界】给队列总长度（所有点入队总次数）设置一个上界，

超出上界时直接判定为负环。答案可能错误，但能卡时。

九. 二分图的匹配

还有两个月就要退役的OIER...现在才图论入门QAQ

因为市面上的书都太杂乱了，难度不一、深浅不定...

所以还是决定自已自足、~~咳咳其实是因为不能不学。~~

尽量归纳的完整一些吧，我努力逼自己不要再放弃了w

有什么不对的地方实在无能为力...

毕竟是蒟蒻...毕竟快要退役了...

无论如何就加油吧√ 作为竹简怎么能放弃呢是吧...

——时间划过风的轨迹，那个少年，还在等你。