正题

我就以这一题：玩具装箱装玩具来引入我们今天的话题。

我们先设f[i]表示前i个玩具装的最小费用是多少。

那么，很明显就有我们枚举一个j，使得j+1到i装在一起，那么就有下面的方程。

$\\f[i]=min(f[j]+(i-j-1+sum[i]-sum[j]-L)^2) \\f[i]=min(f[j]+((sum[i]+i)-(sum[j]+j+L+1)))$

然后我们使 $a[i]=sum[i]+i,b[i]=sum[i]+i+L+1$

那么就有

$\\f[i]=min(f[j]+(a[i]-b[j])^2) \\f[i]=min(f[j]+a[i]^2-2a[i]b[j]+b[j]^2) \\f[i]=min(f[j]-2a[i]b[j]+b[j]^2)+a[i]^2 \\f[i]=min(-2a[i]b[j]+(f[j]+b[j]^2))+a[i]^2$

上面的推导过程是很明显的。

接着，我们设 $k=-2a[i],x=b[j],y=f[j]+b[j]^2$

那么就有

$f[i]=kx+y+a[i]^2$

我们现在已知 $a[i]^2,k$ ，要找到一组x和y使得f[i]最小。

我们先把a[i]^2丢掉，就剩下：

$\\f[i]=kx+y \\y=f[i]-kx \\y=-kx+f[i]$

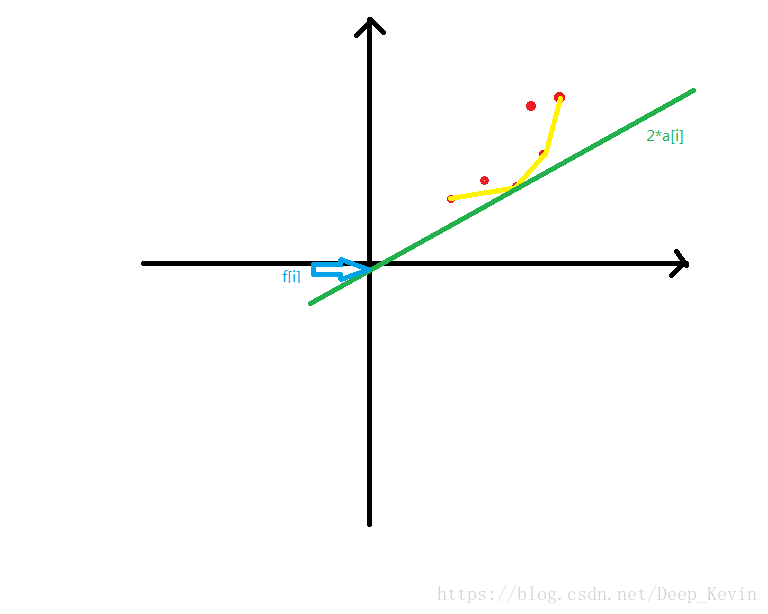
现在就像一条公式了，所以要使f[i]最小，就相当于让一条斜率为-k (2*a[i]) 的直线，从无穷小往上平移，碰到的第一个点就是要求的x和y。明显这个点肯定在1到i-1的下凸包上，又因为a[i]是递增的，所以决策一定是单调上升的。

那么证明了决策单调性，可以用常规方法，也可以用维护凸包的方法，维护一下就好了，就像下图，我们每一次选中的点一定是对于这个斜率的“凸”点。如果有兴趣的同学可以用四边形不等式来证明一下。

下面是代码，这道题不知道为什么，算斜率的时候用double是错的，long long 却是对的。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
using namespace std;

int n,m;
long long a[50010],b[50010],f[50010];
struct node{
	long long x,y;
}s[50010],now;
int st=1,ed=1;

long long get_k(node x,node y){
	return (x.y-y.y)/(x.x-y.x);
}

int main(){
	scanf("%d %d",&n,&m);
	int x,sum=0;
	a[0]=0;b[0]=m+1;
	s[st]=(node){b[0],b[0]*b[0]};
	for(int i=1;i<=n;i++){
		scanf("%d",&x);
		sum+=x;
		a[i]=sum+i;b[i]=sum+i+m+1;
	}
	for(int i=1;i<=n;i++){
		while(st<ed && get_k(s[st],s[st+1])<=2*a[i]) st++;
		f[i]=-2*a[i]*s[st].x+s[st].y+a[i]*a[i];
		now=(node){b[i],f[i]+b[i]*b[i]};
		while(st<ed && get_k(s[ed-1],s[ed])>=get_k(s[ed],now)) ed--;
		s[++ed]=now;
	}
	printf("%lld\n",f[n]);
}

有一篇好论文：https://wenku.baidu.com/view/eeb6d3ea19e8b8f67c1cb937.html

四边形不等式：如果状态x转移到状态y的代价为w[x,y]，只要满足

$w[ x , y ] + w[ x+1 , y+1 ]<=w[x+1,y]+w[x,y+1]$