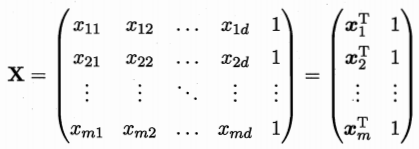线性回归模型

线性函数的定义如下：
$h(\bm{x})=w_{1}x_{1}+w_{2}x_{2}+...+w_{d}x_{d}+b=\bm{w}^{T}\bm{x}+b$
给定数据集 $D=\{(\bm{x}_{i},y_{i})\}_{1}^{N}$，其中 $\bm{x}_{i},y_{i}$都是连续型变量。线性回归试图去学习到 $h(\bm{x})$能准确地预测 $y$。
回归任务最常用的性能度量就是均平方误差(MSE,mean squared error):
$J(\bm{w},b)=\frac{1}{2}\sum_{i=1}^{N}(y_{i}-h(\bm{x}_{i}))^{2}=\frac{1}{2}\sum_{i=1}^{N}(y_{i}-\bm{w}^{T}\bm{x}_{i}+b)^{2}$
参数的优化：（入门人士只需掌握（1）即可，实用简单）
（1）可以使用梯度下降来优化误差，每一步的更新为：
$w_{j}:=w_{j}-\eta \frac{\partial J(\bm{w},b)}{\partial w_{j}}=w_{j}-\eta \sum_{i=1}^{N}(y_{i}-h(\bm{x}_{i}))\bm{x}_{i}^{j},j=1,2,...d \\ b:=b-\eta \frac{\partial J(\bm{w},b)}{\partial b}=w_{j}-\eta \sum_{i=1}^{N}(y_{i}-h(\bm{x}_{i})),j=1,2,...d$
(2)最小二乘估计：
将 $\bm{w}$和 $b$合起来写为 $\hat{\bm{w}}=(\bm{w};b),$把数据集表示为 $N\times (d+1)$的矩阵，前 $d$个元素对应属性值，最后一个数为 $1$对应参数 $b$。

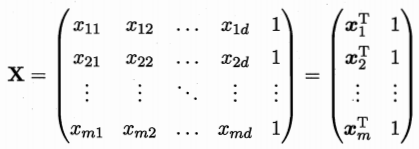
标记也写为向量的形式： $\bm{y}=(y_{1};y_{2};...;y_{N})$,则求最小化误差的参数 $\hat{\bm{w}}$可表示为：
$\hat{\bm{w}}^{*}=\min_{\hat{\bm{w}}}J(\hat{\bm{w}})=\min_{\hat{\bm{w}}}(\bm{y}-\mathbf{X}\bm{\hat{w}})^{T}(\bm{y}-\mathbf{X}\bm{\hat{w}})$
$\frac{\partial J(\hat{\bm{w}})}{\partial\hat{\bm{w}}}=0 \\ \Rightarrow 2\mathbf{X}^{T}(\mathbf{X}\hat{\bm{w}}-\bm{y})=0$
当 $\mathbf{X}^{T}\mathbf{X}$为满秩矩阵（判断矩阵是否可逆的充要条件）或正定矩阵时，上式可解为：
$\hat{\bm{w}}=(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\bm{y}$
此时的回归模型为：
$h(\bm{x}_{i})=\bm{x}_{i}^{T}(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\bm{y}$
当 $\mathbf{X}^{T}\mathbf{X}$不是满秩矩阵时，相当于求线性方程组 $(\mathbf{X}^{T}\mathbf{X})\hat{\bm{w}}=\mathbf{X}^{T}\bm{y}$,此时可能解出多个 $\hat{\bm{w}}$，它们都能使得误差均方误差最小化（所得到的误差都是相同的）。选择哪个将由算法决定，通常引入正则化项来解决。
当加入正则项时，误差为：
$\hat{\bm{w}}^{*}=\min_{\hat{\bm{w}}}J(\hat{\bm{w}})=\min_{\hat{\bm{w}}}[(\bm{y}-\mathbf{X}\bm{\hat{w}})^{T}(\bm{y}-\mathbf{X}\bm{\hat{w}})+\frac{\lambda}{2}||\hat{\bm{w}}||^{2}]$
$\hat{\bm{w}}=(\mathbf{X}^{T}\mathbf{X}+\lambda \mathbf{I})^{-1}\mathbf{X}^{T}\bm{y}$
(3)最大似然估计
设 $\epsilon^{(i)}$为样本 $i$的误差，则有：
$y^{(i)}=\bm{w}^{T}\bm{x}^{(i)}+\epsilon^{(i)},i=1,2,...,N$
$\epsilon^{(i)}$与 $\epsilon^{(j)},i \neq j$之间独立同分布，都满足正态分布 $\epsilon^{(i)}\sim \mathcal{N}(0,\sigma^{2}),i=1,2,...,N$
$p(\epsilon^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(\epsilon^{(i)})^{2}}{2\sigma^{2}})$
因为 $\epsilon^{(i)}=y^{(i)}-\bm{w}^{T}\bm{x}^{(i)}$， $\epsilon^{(i)}$的概率就是 $\bm{x}^{(i)}$能映射到 $y^{(i)}$的概率。
$p(y^{(i)}|\bm{x}^{(i)};\bm{w})=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y^{(i)}-\bm{w}^{T}\bm{x}^{(i)})^{2}}{2\sigma^{2}})$
最大化似然函数：
$L(\bm{w})=\prod_{i=1}^{N}p(y^{(i)}|\bm{x}^{(i)};\bm{w})$
取对数似然：
$\log{L(\bm{w})}=\sum_{i=1}^{N}\log(p(y^{(i)}|\bm{x}^{(i)};\bm{w}) \\ =\sum_{i=1}^{N}\log[\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y^{(i)}-\bm{w}^{T}\bm{x}^{(i)})^{2}}{2\sigma^{2}})]\\ =\sum_{i=1}^{N}[-\frac{1}{2}\log{(2\pi)-\log{\sigma}-\frac{(y^{(i)}-\bm{w}^{T}\bm{x}^{(i)})^{2}}{2\sigma^{2}}}]\\ =-N\frac{1}{2}\log{(2\pi)-N\log{\sigma}-\frac{1}{2\sigma^{2}}}\sum_{i=1}^{N}(y^{(i)}-\bm{w}^{T}\bm{x}^{(i)})^{2}$
最大化对数似然函数等价于最小化均方误差。