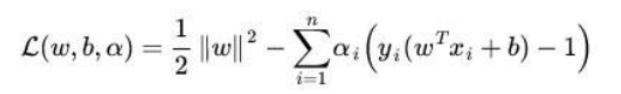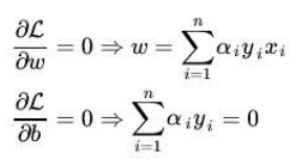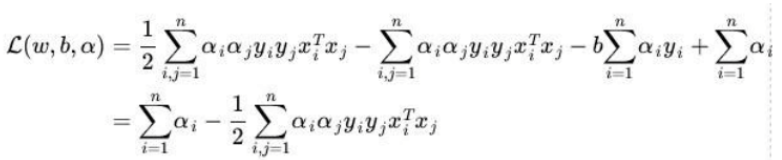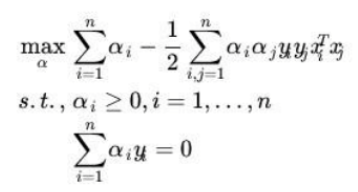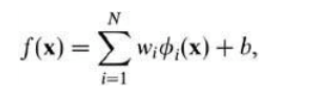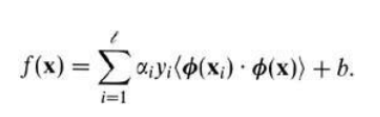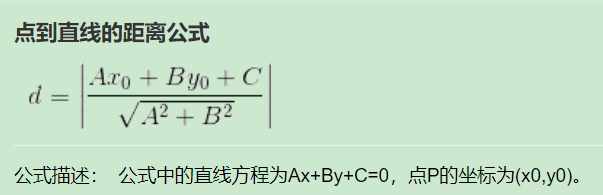1.模型表示

寻找一个超平面 $w^Tx+b=0$能够将训练样本正确分类，也就是满足:
$y_i(w^Tx_i+b)=|f(x_i)|>=1 \tag1$
即：

• 当 $y_i=+1$时， $w^Tx_i+b>=+1$
• 当 $y_i=-1$时， $w^Tx_i+b<=-1$

样本点到超平面上的距离（点到直线的距离公式）：
$\gamma_{geo}= \quad \frac{|w^Tx+b|}{||w||}$

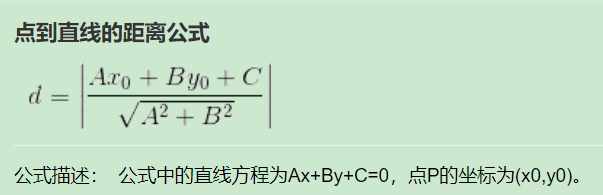
A=w，B=0，C=b

函数间隔与几何间隔
函数间隔： $\gamma_{fun}=y(w^Tx+b)=yf(x)=|f(x)|$
几何间隔： $\gamma_{geo}=\frac{|w^Tx+b|}{||w||}=\frac{|f(x)|}{||w||}=\frac{\gamma_{fun}}{||w||}$

两个异类支持向量（使得式1中等号成立的样本点）到超平面的距离之和：
$\gamma= \quad \frac{2}{||w||}$
目标：最大化间隔<=>最小化 $||w||^2$
因此，SVM模型表示为：
$min \quad ||w||^2 \tag2$ $s.t. \quad y_i(w^Tx_i+b) \ge 1 \quad i=1,...,m$

2.模型求解

参考本人博客《拉格朗日乘子法和KKT条件》
https://blog.csdn.net/weixin_38493025/article/details/84176756
第3节：不等式条件下求解最优问题【KKT条件】

构造拉格朗日函数，

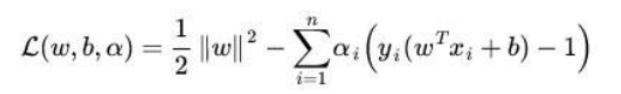
利用KKT条件求解

1. L关于w，b的偏导为0
2. $\alpha_i\ge0,\quad i=1,...,n$
3. $\alpha_ig(x_i)=\alpha_i(1-y_i(w^Tx_i+b))=0$

如果 $\alpha_i=0$，条件3自然成立；
如果 $\alpha_i\ne0$，为了满足条件3，则必须有 $y_i(w^Tx_i+b)=1$，此时的样本即为支持向量，我们的目标就是找出这些支持向量对应的 $\alpha_i$

令偏导为0

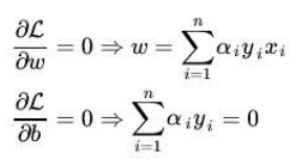
代入拉格朗日函数L中，得到

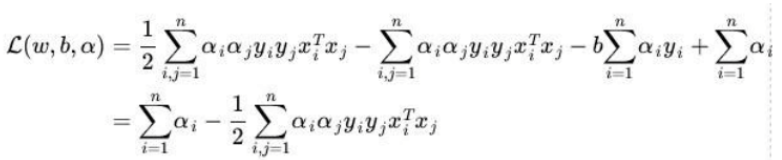
因此，原始问题的对偶问题为：

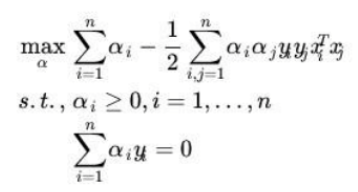
只要求出拉格朗日乘子a，则由 $w=\sum_{i=1}^n\alpha_iy_ix_i$可得w，由 $wx+b=0$则得b。

拉格朗日乘子a的求解

解法1：拉格朗日乘子法（慢）

对偶问题的约束条件为等式约束，再次运用拉格朗日乘子法即可求解a

参考本人博客《拉格朗日乘子法和KKT条件》
https://blog.csdn.net/weixin_38493025/article/details/84176756
第2节：等式条件下求解最优问题【拉格朗日乘子法】

解法2：SMO算法（快）

参考：http://bitjoy.net/2016/05/02/svm-smo-algorithm/

SMO算法通过启发式方法选择一对 $α_i、α_j$当变量，固定其他参数 $α_k$，然后用解析的方法求解两个变量的二次规划问题。

乘子的选择（启发式方法）：

3.非线性形式

对于非线性的情况，选择恰当的核函数代替内积，通过将数据映射到高维空间，在这个空间中构造最优超平面，解决在原始空间中线性不可分的问题。（如果原始空间是有限维，那么一定存在一个高维特征空间使得样本线性可分。）

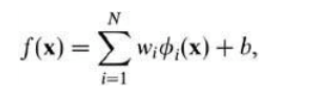
对偶形式：

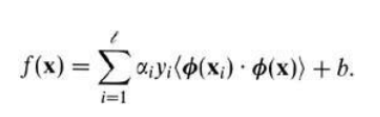
计算内积：
寻找一个合适的二元函数，它的输入是原空间的两个向量，它的输出是映射到高维空间的两个向量的内积，这个函数就是核函数，表示为：
$K(x,z)=&lt;\phi(x),\phi(z)&gt;$
常用核函数：

4.SVM的变形

4.1软间隔支持向量机

在式(2)里面是要求超平面能够将训练样本正确分类（称为“硬间隔”），事实上我们可以允许某些样本不满足约束 $y_i(w^Tx_i+b)\ge1$，当然在最大化间隔的同时这类样本要尽可能地少。
模型表示为：
$\min_{w,b}\quad \frac{1}{2}||w||^2+C\sum_{i=1}^mmax(0,1-y_i(w^Tx_i+b))\tag3$
当C无限大时，模型退化为硬间隔SVM。
软间隔SVM 的损失函数可以看作是 L2-norm 和 Hinge loss 之和。Hinge损失 $l_{hinge}(z)=max(0,1-z)$表示如果被正确分类，损失是0，否则损失就是 1−z 。
引入松弛变量 $\xi_i\ge0$，式(3)可以重写为：
$\min_{w,b,\xi} \quad \frac{1}{2}||w||^2+C\sum_{i=1}^m\xi_i\tag4$ $s.t \quad y_i(w^Tx_i+b)\ge1-\xi_i$ $\xi_i\ge0,\quad i=1,...,m$

4.2 模糊支持向量机

4.2.1 基于标准模型的模糊支持向量机

在实际应用中，数据集常常带有孤立点或噪声。然而，标准支持向量机对噪声点或孤立点敏感，因此就有学者通过对不同的样本赋予不同的误差权重，提出了基于标准模型的模糊支持向量机。
$\min_{w,b,\xi} \quad \frac{1}{2}||w||^2+C\sum_{i=1}^ms_i\xi_i\tag5$ $s.t \quad y_i(w^Tx_i+b)\ge1-\xi_i$ $\xi_i\ge0,\quad i=1,...,m$

4.2.2 双边加权模糊支持向量机

考虑到在实际问题中，一个样本可能以不同的隶属度属于不同的类，有学者提出了双边加权模糊支持向量机。
$\min_{w,b,\xi} \quad \frac{1}{2}||w||^2+C\sum_{i=1}^m(s_i^+\xi_i^++s_i^-\xi_i^-)\tag6$ $s.t \quad y_i(w^Tx_i+b)\ge1-\xi_i^+$ $\quad y_i(w^Tx_i+b)\le-1+\xi_i^-$ $\xi_i\ge0,\eta_i\ge0,\quad i=1,...,m$

4.2.3 双边加权模糊最小二乘支持向量机

为了解决带噪声的回归问题，将目标函数中 $\xi_i$变成 $\xi_i^2$，用等式约束代替不等式约束，有学者提出了双边加权最小二乘模糊支持向量机。
$\min_{w,b,\xi} \quad \frac{1}{2}||w||^2+\frac{C}{2}\sum_{i=1}^m(s_i^+\xi_i^{+^2}+s_i^-\xi_i^{-^2})\tag7$ $s.t \quad y_i(w^Tx_i+b)=1-\xi_i^+$ $\quad y_i(w^Tx_i+b)=-1+\xi_i^-$ $\xi_i\ge0,\eta_i\ge0,\quad i=1,...,m$