1. 总体、个体和样本

在使用数理统计方法研究某个实际问题时，往往把所研究对象的全体称为总体，而把组成总体的每个基本单位称为个体。

例如：某一批灯泡组成一个总体，而每个灯泡都称为个体；又如某个学校的所有学生被称为总体，每个学生都称为个体。

在数理统计中，总体或者是个体本身并不是我们所关心的，我们关心的是它们的某个特性或者说某个指标，如灯泡的寿命、学生的身高等，寿命和身高都是随机变量。

当我们需要对总体的某个特征进行研究时，往往不能对所有个体进行试验，一种可行的方法就是对总体进行抽样调查。数理统计的基本任务就是通过抽样结果来推断总体的统计规律。

对总体，把在相同条件下对随即变量X进行的n次重复独立观察，成为n次简单随机抽样，简称简单抽样。用X_i表示第i次观察结果，那么对总体X的n次重复独立观察所得结果记为X₁，X₂，…，X_n。每个X_i都是一个与总体X有相同分布的随机变量，且X₁，X₂，…，X_n相互独立，称随机变量X₁，X₂，…，X_n为来自总体X的简单随机样本，简称简单样本。

抽样观察的结果是n个具体数值x₁，x₂，…，x_n，称其为简单样本X₁，X₂，…，X_n的一组观察值，成为样本观察值。

一般来说，不同的抽样得到样本X₁，X₂，…，X_n的不同观察值，样本所有可能取值的全体称为样本空间，用Ω表示，样本观察值实际就是样本空间中的一个点，称其为样本点。

例如：把一枚硬币重复独立的掷三次，正面记为1，反面记为0。用X₁，X₂，X₃表示三次可能的结果，可知样本空间Ω=
{(0，0，0)，(0，0，1)，(0，1，0)，(0，1，1)，(1，0，0)，(1，0，1)，(1，1，0)，(1，1，1)}。样本观察值可能为(0，1，1)，它是样本空间中的一个样本点。

此外，样本的数量称为样本容量。

2. 统计量与充分统计量

统计量

我们知道，样本是总体的代表和反映，是对总体进行统计分析和推断的依据。因此，为了提取出样本中有关总体的信息，我们需要引入统计量的概念。

统计量是样本的函数，它的作用是汇集样本中有关总体的信息。

值得特别注意的是：统计量仅为样本 $X_1, X_2, ...X_n$的函数，它不包含总体的任何未知量。这一点非常重要，是理解、求解和利用统计量的重点。

下面给出统计量的定义：
定义1： 设 $X_1, X_2, ... X_n$为来自总体X的简单样本，若样本的函数 $T(X_1, X_2, ... X_n$中不包含任何未知参数，则称此函数为统计量。

例如， $\displaystyle\bar{X}=\frac{1}{n}\sum_{i=1}^{n}X_i$仅为样本 $X_1, X_2, ... X_n$的函数，因此它是统计量；而 $\displaystyle\frac{1}{n}\sum_{i=1}^{n}(X_i-\mu)^2$中包含未知参数 $\mu$，因此它不是统计量。

常用统计量

下面介绍几个常用的统计量。设 $X_1, X_2, ... X_n$为来自总体X的简单样本。

(1) 统计量 $\displaystyle\bar{X}=\frac{1}{n}\sum_{i=1}^{n}X_i$称为样本均值，它反映了样本的平均取值，描述了样本的集中取值趋势。

(2) 统计量 $\displaystyle S^2=\frac{1}{n-1}\sum_{i=1}^{n}{(X_i-\bar{X})^2}$称为为样本方差，它描述了样本取值的分散程度大小，称 $S$为样本标准差。

(3) 统计量 $\displaystyle A_k=\frac{1}{n}\sum_{i=1}^{n}{X_i^k}$称为样本k阶原点矩。

(4) 统计量 $\displaystyle B_k=\frac{1}{n}\sum_{i=1}^{n}{(X_i-\bar{X})^k}$称为样本k阶中心矩。

顺序统计量

除了样本矩之外，还有一类十分重要的统计量，称为样本顺序统计量，它在数理统计中有着广泛的应用。下面给出样本顺序统计量的定义：

定义2： 将样本 $X_1, X_2, ... X_n$的观察值 $x_1, x_2, ... x_n$按从小到大递增的顺序进行排列，记为 $x_{(1)}, x_{(2)}, ... x_{(n)}$。其中， $x_{(1)}, x_{(2)}, ... x_{(n)}$满足
$x_{(1)}≤x_{(2)}≤ ... ≤x_{(n)}$
定义排在 $k$位置的数 $x{(k)}$为随机变量 $X_{(k)}$的观察值，显然： $X_{(1)}≤X_{(2)}≤ ... ≤X_{(n)}$
由于 $X_{(k)}$是样本 $X_1, X_2, ... X_n$的函数，且不含任何未知数，因此 $X_{(k)}$是统计量。称 $X_{(1)}, X_{(2)}, ... X_{(n)}$为顺序统计量。

特别的， $X_{(1)}$=min $\{X_1, X_2, ... X_n\}$ 表示样本 $X_1, X_2, ... X_n$中取最小值，其观察值是样本观察值中最小的一个。 $X_{(n)}$=max $\{X_1, X_2, ... X_n\}$ 表示样本 $X_1, X_2, ... X_n$中取最大值，其观察值是样本观察值中最大的一个。

注意： 统计量是随机变量的函数，因此统计量也是随机变量，统计量的分布称为抽样分布。下面讨论 $X_{(1)}$和 $X_{(n)}$的分布函数。

设 $X_1, X_2, ... X_n$为总体X的简单样本，总体X的分布函数为F(x)，根据分布函数的定义：
$\begin{aligned} F(X_{(1)}<x) &=1-F(X_{(1)}≥x)\\ &=1-F(X_{(n)}≥...≥X_{(2)}≥X_{(1)}≥x) \\&=1-F(X_{(n)}≥x)...F(X_{(2)}≥x)·F(X_{(1)}≥x) \\&=1-[1-F(X_{(n)}＜x)]...[1-F(X_{(2)}＜x)]·[1-F(X_{(1)}＜x)] \\&=1-[1-F(x)]^n \end{aligned}$
记作： $F_{X_{(n)}}(x)=1-[1-F(x)]^n$
同理可求得： $F_{X_{(1)}}(x)=F^n(x)$

基于顺序统计量，我们可以构造一些常用的统计量，如样本极差，样本分位数等。

(1) 样本极差：样本极差定义为R= $X_{(n)}-X_{(1)}$，同样本方差类似，它也可以用来描述样本的分散程度。
(2) 样本分位数：样本的p（0＜p＜1）分位数 $m_p$定义为：
$m_p=\begin{cases} X_{([np+1])} & np不为整数 \\\frac{1}{2}(X_{(np)}+X_{(np+1)}) & np为整数 \end{cases}$
其中， [x]表示取不超过数x的最大整数。
注1：若将样本观察值从小到大进行排序，p分位数 $m_p$的意义是排在它前的观察值个数约占观察值总数的p%。
注2：一般情况下，要给出 $m_p$的精确分布是很困难的，但当样本容量n很大时，可以证明 $m_p$为渐近正态。
注3：样本极差和样本分位数都是随机变量，理解这一点非常重要。

充分统计量

下面将介绍充分统计量的概念，为了便于理解，先看下例：

例1：掷硬币试验，设正面出现的概率为 $\theta$，总体X的分布族为 $\{P_{\theta}:\theta∈(0, 1)\}$，其中 $P_{\theta}\{X=x\}=\theta^x(1-\theta)^{1-x}，x_i=0,1$。设 $X_1, X_2, ... X_n$是来自总体X的简单样本，样本空间 $S=\{(x_1, x_2, ..., x_n):x_i=0,1,i=1, 2, ..., n\}$,它包含了 $2^n$个样本点。

对于上述问题，总体X服从两点分布，因此 $\theta$实际上反映的是正面出现的概率。当样本数量足够多时，我们也可以说 $\theta$决定了正面出现的次数，这可以由样本点 $(x_1, x_2, ..., x_n)$中1的个数来体现。同样的，样本点 $(x_1, x_2, ..., x_n)$中1的个数也很好的体现了 $\theta$的信息。

下面考虑统计量 $\displaystyle T=\sum_{i=1}^nX_i$，它是样本 $X_1, X_2, ... X_n$的函数，提取了样本点中"1"的个数信息，剔除了样本带你中"1"的位置信息，起到了很好的信息压缩作用。同时，样本点中"1"的个数信息正好是参数 $\theta$的全部信息，因此T既起到了提取参数 $\theta$的全部信息的作用，也起到了剔除了无关信息的作用。

为了理解一个统计量包含了样本中有关某参数的全部信息这一个说法，可以通过下面的例子来说明：

例2：当我们用样本均值 $\bar{X}$估计总体均值 $\mu=EX$时，用 $\bar{X}$的观察值 $\bar{x}$作为 $\mu$的估计值，这时统计量 $\bar{X}$已经包含了样本中有关参数 $\mu$的所有信息，当我们进一步知道 $(X_1,X_2, ...X_n)$中任何一个变量的取值时并不能帮助我们获取参数 $\mu$的更多信息。换句话说，对于样本中关于参数 $\mu$的信息，我们不需要记录所有样本的取值，只需要记录 $\bar{X}$即可。

也就是说，当我们用样本来估计总体的某个参数时，不需要分析样本的所有信息，只需要找到一个关于该参数的充分统计量即可，因为该统计量包含了样本中关于该参数的全部信息。

下面举一个更加具体的例子：

设总体X服从正态分布 $N(\mu, 1)，\mu$是需要估计的未知参数， $X_1, X_2$是来自总体的样本，用样本均值 $\displaystyle \bar{X}=\frac{1}{2}(X_1+X_2)$来估计 $\mu$。这时样本空间 $S$为平面区域，当给定 $\bar{X}$=a时， $\displaystyle \frac{1}{2}(X_1+X_2)=a$表示样本空间 $S$中的一条直线：

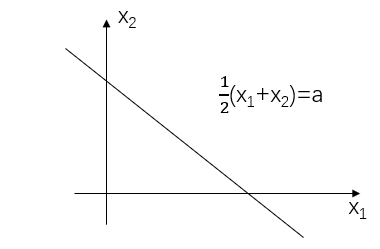
$(X_1, X_2)$服从二维正态分布 $N(\mu, 1;\mu, 1;0)$,其密度函数为：
$p(x_1, x_2;\mu)=\frac{1}{2\pi}exp\{-\frac{1}{2}\sum_{i=1}^{2}(x_i-\mu)^2\}$
样本均值 $\displaystyle \bar{X}=\frac{1}{2}(X_1+X_2)$服从正态分布 $\displaystyle N\{\mu, \frac{1}{2}\}$，其密度函数为：
$p(a;\mu)=\frac{1}{\sqrt\pi}exp\{-(a-\mu)^2\}$
在直线 $\bar{X}=a$上， $(X_1, X_2)$的分布可以用条件密度函数
$\displaystyle p(x_1, x_2|\bar{x}=a)=\begin{cases} \frac{p(x_1, x_2;\mu)}{p(a;\mu)} &\bar{x}=a \\0 & \bar{x}≠a \end{cases}$
来描述，其中 $\bar{x}$为 $\bar{X}$的观察值，而a为 $\bar{X}$的给定值。所以
$\displaystyle p(x_1, x_2|\bar{x}=y)=\begin{cases} \displaystyle \frac{1}{2\sqrt\pi}exp\{-\frac{1}{2}\sum_{i=1}^{2}(x_i-a)^2 & \bar{x}=a \\0 & \bar{x}≠a \end{cases}$
由上面的条件密度函数的表达式可知，它与参数 $\mu$无关，这表明在已知 $\bar{x}=y$时，如果进一步知道样本的观察值 $(x_1, x_2)$在这条直线上的具体位置，也并没有增加关于参数 $\mu$的任何新信息。换句话说， $\bar{x}$已充分提取了样本 $X_1, X_2$关于参数 $\mu$的全部信息，因此 $\bar{X}$是参数 $\mu$的充分统计量。

根据上面的解释，根据概率论中的条件分布给出充分统计量的定义：

定义： 设总体分布族为 $\{P_\theta:\theta\in\Theta\}，X_1, X_2, ..., X_n$是来自总体的简单样本，样本的函数 $T\{X_1, X_2, ...X_n\}$是统计量。如果在给定 $T\{X_1, X_2, ...X_n\}$=t的条件下，样本X_1, X_2, …X_n的条件分布函数 $F_\theta(x_1, x_2, ... x_n|t)$与参数 $\theta$无关，则称统计量 $T\{X_1, X_2, ...X_n\}$为参数 $\theta$的充分统计量。

注： 由于条件分布函数与条件分布列或条件密度函数是一一对应的，因此可以用条件分布列或者条件密度函数来代替上面的条件分布函数。

例3：掷硬币试验，设正面出现的概率为 $\theta$，总体X的分布族为 $\{P_{\theta}:\theta∈(0, 1)\}$，其中 $P_{\theta}\{X=x\}=\theta^x(1-\theta)^{1-x}，x_i=0,1$。设 $X_1, X_2, ... X_n$是来自总体X的简单样本，求 $\theta$的充分统计量

解：总体X的分布律为： $\{P_{\theta}:\theta∈(0, 1)\}$
样本的联合分布列为：
$\displaystyle P(x;\theta )=\theta^{\sum_{i=1}^{n}x_i}(1-\theta)^{n-\sum_{i-1}^{n}x_i}$
其中 $x_i=0或1$.给定 $T=\sum_{i-1}^{n}X_i=t$的条件下，样本 $X_1, X_2, ... X_n$的条件分布列为：
$\begin{aligned} P(x;\theta )&=\frac{P\{X_1=x_1,X_2=x_2,..., X_n=x_n, \sum_{i=1}^{n}X_i=t\}}{P\{\sum_{i=1}^{n}X_i=t\}} \\&=\frac{\theta^t(1-\theta)^{n-t}}{C_n^t\theta^t(1-\theta)^{n-t}} \\&=\frac{1}{C_n^t} \end{aligned}$
因此，条件分布列与参数 $\theta$无关，由定义，统计量 $T=\sum_{i-1}^{n}X_i$是充分统计量。

一般情况下，利用条件分布直接证明给定的统计量是否是充分统计量是比较困难的。下面给出一个定理来求解样本的充分统计量。

定理（Fisher-Neyman准则）：设总体分布族为 $\{ P_{\theta}:\theta\in\Theta\}$，则统计量 $T(x)$是充分统计量的，当且仅当存在一个定义在 $I\times\Theta$上的实值函数 $g(t, \theta)$及定义在样本空间 $S$上的不依赖于参数 $\theta$的实值函数 $h(x)$使样本 $x_1, x_2, ...x_n$的联合分布 $p(x;\theta)$的分解式
$p(x;\theta)=g(T(x), \theta)h(x)$
对所有的 $x\in S$都成立，其中 $I$是统计量 $T(x)$的值域， $p(x, \theta)$是样本的联合分布列或密度函数。

例4. 设 $x_1, x_2, ...x_n$是来自Possion分布总体 $P(x;\lambda)$的简单样本，求参数 $\lambda$的充分统计量。

解：泊松分布的分布律为：
$P\{X=k\}=\frac{\lambda^k}{k!}e^{-\lambda}，k=0, 1, ...$
则样本的联合分布列为：
$\begin{aligned} p(x_1, x_2, ...x_n;\lambda)&=\frac{e^{-n\lambda}}{x_1!x_2!...x_n!}\lambda^{\sum^n_{i=1}x_i} \\&=(e^{-n\lambda}\lambda^{\sum^n_{i=1}x_i})\frac{e^{-n\lambda}}{x_1!x_2!...x_n!} \end{aligned}$
取 $T(x)=\sum_{i=1}^nx_i=t，g(t, \lambda)=e^{-n\lambda}\lambda^t，h(x)=\frac{e^{-n\lambda}}{x_1!x_2!...x_n!}$
由定理得 $T(x)=\sum_{i=1}^nx_i$为参数 $\lambda$的充分统计量。

下面是一个多参数的例子：

例5. 设 $x_1, x_2, ...x_3$是来自正态总体 $N(\mu, \sigma^2)$的简单样本，其中 $\mu和\sigma^2$都是未知的，试求参数 $\theta=(\mu, \sigma^2)$的完全统计量。

解：样本的联合密度函数为：
$\begin{aligned} p(x_1, x_2...x_n;\theta)&=(\frac{1}{\sqrt{2\pi\sigma^2}})^nexp\{-\frac{1}{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2\} \\&=(\frac{1}{\sqrt{2\pi\sigma^2}})^nexp\{-\frac{1}{2\sigma^2}(\sum_{i=1}^nx_i^2-2\mu\sum_{i=1}^nx_i+n\mu^2)\} \end{aligned}$
取 $T(x)=(T_1(x), T_2(x))=(\sum_{i=1}^nx_i, \sum_{i=1}^nx_i^2)，h(x)\equiv1$及
$g(t, \theta)=(\frac{1}{\sqrt{2\pi\sigma^2}})^2exp\{-\frac{1}{2\sigma^2})(t_2-2\mu t_1+n\mu^2)\}$
其中， $t=(t1, t2)$，则有
$p(x_1, x_2, ...x_n;\theta)=g(t, \theta)h(x)$
由定理得， $T(x)=(\sum_{i=1}^nx_i, \sum_{i=1}^nx_i^2)$是 $\theta$的充分统计量。
又因为样本的联合密度函数可表示为：
$\begin{aligned} p(x_1, x_2...x_n;\theta)&=(\frac{1}{\sqrt{2\pi\sigma^2}})^nexp\{-\frac{1}{2\sigma^2}\sum_{i=1}^n(x_i+\bar{X}-\bar{X}-\mu)^2\} \\&=(\frac{1}{\sqrt{2\pi\sigma^2}})^nexp\{-\frac{1}{2\sigma^2}[\sum_{i=1}^n(x_i-\bar{x})^2+n(\bar{x}-\mu)^2]\} \end{aligned}$
可取 $S(x)=(S_1(x), S_2(x))=(\sum_{i-1}^{n}x_i, \sum_{i=1}^n(x_i-\bar{x}), h(x)\equiv1$及
$g(s, \theta)=(\frac{1}{\sqrt{2\pi\sigma^2}})^nexp\{-\frac{1}{2\sigma^2}[s_2+n(\frac{s_1}{n}-\mu)^2]\}$
由定理得， $S(x)=(\sum_{i-1}^{n}x_i, \sum_{i=1}^n(x_i-\bar{x}), h(x)\equiv1$是 $\theta$的充分统计量。

上例说明，参数 $\theta$的充分统计量是不唯一的。另一方面，当参数的维数和充分统计量的维数相等时，应当将充分统计量看作是一个有机的整体，不能拆分，认为充分统计量的分量是相应参数向量的分量的充分统计量是错误的。

下面再举一个例子，通过下面这个例子我们可以看到，顺序统计量有时候也是充分统计量。

例6. 设 $x_1, x_2, ...x_n$是来自均匀分布总体U[a, b]的简单样本，其中a和b都是未知的，且a<b，令参数 $\theta=(a, b)$，求 $\theta$的充分统计量。

解：样本的联合密度函数为：
$\begin{aligned} p(x_1, x_2, ...x_n)&amp;=\frac{1}{(b-a)^n}I_{\{a\le x_{(1)}\le x_{(n)}\le b\}}(x_{(1)}, x_{(2)}, ...x_{(n)}) \\&amp;=\frac{1}{(b-a)^n}I_{\{a\le x_{(1)}\le x_{(n)}\le b\}}(x_{(1)}, x_{(n)}) \end{aligned}$
其中
$I_A(u)=\begin{cases}1,&amp;u\in A \\ 0, &amp;u\notin A \end{cases}$
称其为示性函数。
令 $T(x)=(x_{(1)},x_{(n)})，g(t, \theta)=\frac{1}{(b-a)^n}I_{\{a\le t_1\le t_2\le b\}}(t_1, t_2)，h(x)\equiv1$
其中， $t=(t_1, t_2)$，则联合密度函数有分解式
$p(x_1, x_2, ...x_n;\theta)=g(t, \theta)h(x)$
由定理知， $T(x)=(x_{(1)},x_{(n)})$是参数 $\theta$的充分统计量。

最后需要提及的是，对一个分布族 $\{P_\theta:\theta\in\Theta\}$而言，充分统计量往往不是唯一的，都包含样本中关于参数的全部信息，但它们在压缩数据能力方面是不同的。例如：对于两点分布族，统计量 $(x_1, x_2, ...x_n)$和统计量 $\sum_{i=1}^nx_i$都是充分统计量，都保留了与参数 $\theta$有关的“1”的个数的信息，但是在剔除无关信息方面， $\sum_{i=1}^nx_i$好得多。因此，我们往往需要求的是最小充分统计量。