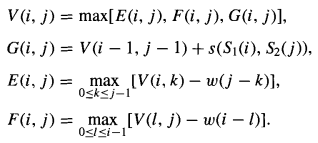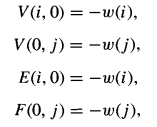字符串的非精确匹配问题(inexact matching),也就是字符串的对齐问题(string alignment)。对于字符串的exact matching问题,KMP、Suffix Tree等方法是利器,但是对于inexact matching,这些方法就有些吃力了,虽然也能使用Suffix Tree解决一些错配问题或通配符问题,但是使用范围很有限。对于inexact matching,一般使用动态规划( Dynamic Programming )处理。DP是老朋友了,时隔6年,好久不见。这里使用的DP比较简单,转移方程容易理解,毕竟是简单的线性DP。
编辑距离(Edit distance)
这道题很经典啊,当初刷这道题时真的没想到今天会从生信的角度来重温,切身体会见证了算法的实用性。
转移方程: D(i, j) = min[D(i - 1, j) + 1, D(i, j - 1) + 1, D(i -i, j-i) + t(i, j)].
初始条件:D(i, 0) = i ,D(0, j) = j.
注:当Si(i) !=S2(j)时,t(i, j)=1; 当S1(i) = S2(j)时,t(i, j)=0.
带权重的编辑距离(Weighted edit distance)
匹配是需要代价或奖励的。所谓权重,有两种类型,第一种是基于基本操作的权重,第二种是基于代价表格的权重。
基于基本操作的权重。对于insertion或deletion给定代价d、对于substitution(replacement)给定代价r,对于match给定奖励e,在此基础上计算编辑距离。
转移方程:D(i, j) = min[D(i, j - 1) + d, D(i - 1, j) + d, D(i - 1, j - 1) + t(i, j)].
初始条件:D(i, 0) = i x d ,D(0, j) = j x d.
基于代价表格的权重。将insertion或deletion看成分别向两个字符串增加空格space(或破折号dash),将两个字符串出现过的所有字符和space(或破折号dash)组成新的集合,对于该集合中的任意两个字符,给出匹配代价s(x,y),得到代价表格s。令V(i,j)表示两个前缀S1[1...i]和S2[1...j]的最优匹配代价。(常常将错配代价记为负值,匹配奖励记为正值,那么此处的匹配代价说成匹配值比较好,并且需要使这个匹配值最大化)
转移方程:V(i, j) = max[ V(i -1,j-1)+ s(S1(i), S2(j)), V(i - 1, j) + s(S1(i), - ), V(i, j-1)+s( _ , S2(j) ) ].
初始条件:
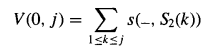
局部匹配(Local alignment)
局部匹配可能是更为常见的问题,比如蛋白质具有特定的功能片段(举例:motif ),有的蛋白质在种间具有进化保守片段,等等问题实际上可以转化为局部匹配的问题。
先看一个定义:局部后缀匹配(Local suffix alignment)。寻找前缀S1[1...i]的后缀a 和前缀S2[1...j]的后缀b,使得匹配值V(a,b)最大化,并记录这个最大化的值为v(i, j)。可以证明,最佳局部匹配的匹配值 vmax = max[v(i, j) : i <= n, j <= m].
转移方程:v(i, j) = max[0, v(i - 1, j - 1) + s(S1(i), S2(j)), v(i -1,j) + s(S1(i),-), v(i, j - 1) + s(-, S2(j)) ].
初始条件:v(i, 0) = 0, v(0, j) = 0.
间隔问题(Gaps)
Gaps也是十分常见的问题,因为在生物序列匹配时,我们可能更关心匹配过程出现了多少个间隔,而不那么关心每个间隔里有多少空格。若出现一个Gap需要代价Wg,出现一个空格需要代价Ws,则出现一个连续m个空格形成的Gap需要代价Wg+m×Ws。利用Gaps模型,我们可以通过调整Wg和Ws的值,来实现不同的匹配效果:当增大Wg时,匹配结果更倾向于Gaps更少、片段更集中; 当增大Ws时,匹配结果更倾向于Gaps更多、片段更零散。
Gaps的权重有四种类型:常数型(constant)、仿射型(affine)、凸面型(convex)、任意型(arbitrary)。
常数型:maximize [Wm(# matches) - Wms(# mismatches) -Wg (# gaps)].
仿射型:maximize [Wm(# matches) - Wms(# mismatches) - Wg(# gaps) - Ws(# spaces)]. (仿射即:y=a+bx)
凸面型:在同一个Gap中,后面增加的space所需的代价比前面的space的代价小。如:Wg+log q(q表示Gap长度)。
任意型:根据Gap的长度不同,Gap总代价值w(q)为任意值(q表示Gap长度),即w(q+1)-w(q)不一定是常数。放射型是任意型的特例。
任意型
首先将匹配情况分为以下三种:
第一种情况,S1[i]与S2[k]对齐(其中k<j),也就是说,此时在S1的第i个位置后增加 (j-k)个空格实现对齐,记这种情况的最优匹配值为E(i ,j)。
第二种情况,S1[k]与S2[j]对齐(其中k<i),也就是说,此时在S2的第j个位置后增加 (i-k)个空格实现对齐,记这种情况的最优匹配值为F(i ,j)。
第三种情况,S1[i]与S2[j]对齐,记这种情况的最优匹配值为G(i ,j)。
记V(i ,j) 为 E(i ,j)、F(i ,j)、G(i ,j)的最大值。
转移方程:
注意:w(q+1)-w(q)不一定是常数。
初始条件:
仿射型
转移条件:
理解:若E(i ,j)由E(i ,j-1)转移而来,则无需新建Gap,也就不需要花费代价Wg。F(i ,j)的理解同理。
初始条件:
凸面型
请参考Algorithms on Strings, Trees and Sequences一书的12.6章节,方法也是基于动态规划。