正题

我们今天讲一下线性规划，以这一道题为例：#179. 线性规划

首先面对一堆小于等于的约束，我们应该怎么做？

我们以样例来解释：

有四条约束，要同时满足： $st.\begin{Bmatrix} 2x_1+x_2\leqslant 6\\ -x_1+2x_2 \leqslant 3 \\ x_1,x_2\geqslant 0\end{Bmatrix}$

同时，我们要使得 $x_1+x_2$ 最大。

首先，我们可以把可行解在一个二维平面上表示出来。

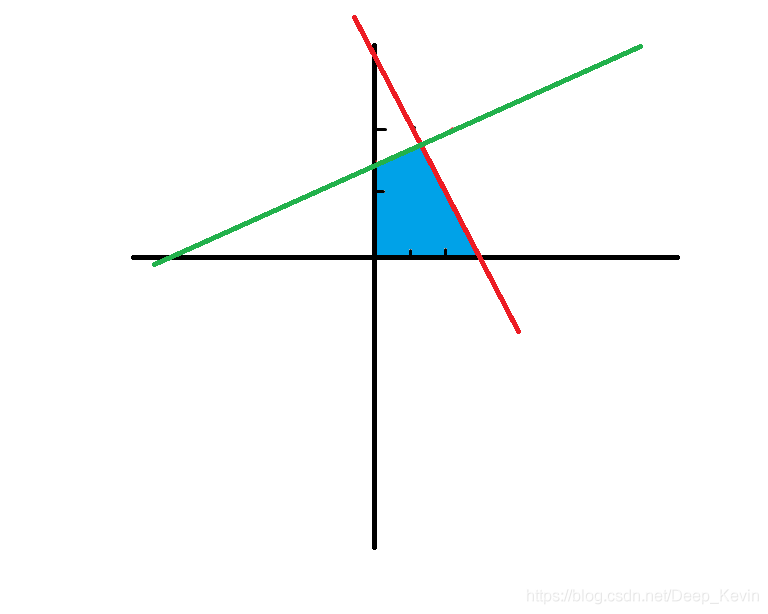
如图，可行解就是蓝色部分，我们要使得 $x_1+x_2$ 最大，那么我们就用一条 $k=-1$ 的直线，从上往下扫，然后，碰到的第一个点就是答案。

这就是图解法。如果有三个变量就是一个立体空间里面，用一个平面从上往下扫就可以了。但是4个变量的时候就难以构建了。

这就是单纯形的应用。

首先我们可以多设两个变量，把小于等于号去掉。

扫描二维码关注公众号，回复： 4358891 查看本文章

$st.\begin{Bmatrix} 2x_1+x_2+x_3 = 6\\ -x_1+2x_2+x_4 = 3 \\ x_1,x_2,x_3,x_4\geqslant 0\end{Bmatrix}$

这个也是没有错的，对吧。

我们把答案也写进去，就变成了。

$\\ans=x_1+x_2\\2x_1+x_2+x_3 = 6\\ -x_1+2x_2+x_4 = 3 \\ x_1,x_2,x_3,x_4\geqslant 0$

再变形一下，就变成：

$\\ans=x_1+x_2\\x_3 = 6-2x_1-x_2\\ x_4 = 3+x_1-2x_2\\ x_1,x_2,x_3,x_4\geqslant 0$

当出现这样的，常数项是非负的，所有的等式右边的变量都是一样的，我们把它叫做基可行解形式。

左边的变量叫做基变量，右边的变量叫做非基变量。

在这个时候，我们构造一组答案是极其简单的，就是让右边的变量全部为0，然后左边的变量就等于右边的常数项，向上面的方程组，有一个显然的解就是 $x_1=0,x_2=0,x_3=6,x_4=3,ans=0$ 。

这组解肯定是可行的，而且我们可以保证这组解一定在集合上的多边形的顶点上。（具体为什么请先继续往下看

我们考虑怎么将答案增大？

我们可以看到， $x_1$ 是非基变量，也就是说，他现在取0.

但是他其实可以取到更大，那它到底能取到多大呢？

就要看下面的约束了，对于第一个约束，他最大能取到3（6/2），对于第二个约束，这个约束对 $x_1$ 是没有约束的，因为在第二个约束中， $x_1$ 不管取到多大，约束都是成立的。

那么我们只能选第一个约束。

那如果我们让 $x_1$ 为3，其他变量最好的情况就是取0。

所以，我们让 $x_1$ 作为基变量，让这个约束原来的基变量换做为非基变量。

$\\ans=x_1+x_2\\x_1 = 3-0.5x_3-0.5x_2\\ x_4 = 3+x_1-2x_2\\ x_1,x_2,x_3,x_4\geqslant 0$

显然这样子还不是基可行解形式，因为 $x_1$ 在两边都出现了。

那我们做一遍高斯消元就可以了！（意思就是把 $x_1=balabala$ 带进其他有 $x_1$ 的地方。

就变成了

$\\ans=3-0.5x_3+0.5x_2\\x_1 = 3-0.5x_3-0.5x_2\\ x_4 = 6-0.5x_3-2.5x_2\\ x_1,x_2,x_3,x_4\geqslant 0$

那我们就得到了一个更大的解 $x_1=3,x_2=0,x_3=0,x_4=6,ans=3$ 。

回想一下，我们刚刚干了些什么？

首先，我们在答案里面，找出了一个系数大于0的非基变量，这个非基变量，我们把它叫做这一次操作的换入变量，接着，我们又找到一个对这个换入变量约束最紧的约束。将它与这条约束原来的基变量进行一个交换，我们把这个基变量叫做换出变量，这个交换叫做转轴。接着，我们用这个式子对每一个式子进行高斯消元。

我们就可以得到一组更大的解。当答案式子中非基变量都小于0了。我们就可以断定答案无法增大了。

如果我们找到了一个大于0的非基变量，但是我们找不到一个约束这个非基变量的约束（系数大于0）。

那么这个约束就可以无限增大，那么就是无最大解（Unbounded）的情况。

我们已经解决了如果有一个基可行解的时候，怎么去找到一个更优的解。

如果我们一开始没有一个基可行解呢？也就是说，如果我们一开始的约束不满足基可行解形式呢？

就像第二个样例：

$\\ans=x_1-x_2 \\x_3=4-x_1-x_2\\x_4=-2+x_1+2x_2 \\x_1,x_2,x_3,x_4\geq 0$

是不满足基可行解的形式的。

存在一种解法，可以检验是否存在一个初始解。这个方法就是给每一条约束的右边都加上一个人工变量A，其中A大于等于0.

然后我们尽量使A小，也就是说当A=0时，才存在一个初始解。

因为给每一条约束右边都加上一个人工变量A就相当于 $x_1+...+x_n<=S_1+A$ ，那么当A=0时，就是原来的约束。

显然，我们只要把答案设为-A就可以了，因为可以使得-A最大，从而使得A最小。

$\\ans=-A \\x_3=4-x_1-x_2+A\\x_4=-2+x_1+2x_2+A \\x_1,x_2,x_3,x_4,A\geq 0$

但是，现在还是不满足基可行解形式的，怎么办呢？

我们选出常数项最小的那一行。将那一行的A转轴成一个基变量。

像上面，我们选出第二个约束。

$\\ans=-2+x_1+2x_2-x_4 \\x_3=6-2x_1-3x_2+x_4\\A=2-x_1-2x_2+x_4 \\x_1,x_2,x_3,x_4,A\geq 0$

现在肯定可以保证所有的约束都满足基可行解形式了。

用单纯形算法来求出A的最小值（-A的最大值）就可以了。

若A=0，那么就有一个初始解，我们将原来的答案序列代入，如果存在一个变量是基变量，那么就先换成非基变量，最后得出第一组解。

若A不等于0，那么说明不存在第一组解，程序结束。

剩下的再交给单纯形算法就可以了。

这样的时间复杂度是很优秀的（随机情况下）。

但是代码量大，不容易实现。

有一种十分玄学的随机做法。

就是对于一个约束，如果常数项小于0，那么我们找到一个正系数的非基变量，将这个非基变量转轴，常数项就大于0了。

如果找不到正系数的非基变量，那么说明就不存在一个解，因为 $x_i = S-x_j (S<0)\to x_i\ngeqslant 0$ 。

那么就很好的完美的解决这类的约束最值问题。

代码

如果真的要把每一条约束的左右两边的存下来，那无疑是非常麻烦的。

其实每一条约束都可以写成 $S = \sum x_i$ 其中S是一个常数。

那么我们就可以写成一个矩阵的形式。 $\bigl(\begin{smallmatrix} S & x_1 & x_2 &... & x_n \end{smallmatrix}\bigr)$

每一行的基变量用一个数组存下来就可以了。

当我们要找一个换入变量的时候，我们还是在第0行找一个正系数的非基变量x。

但是在找一个换出变量的时候，我们要找一行，使得这一行的非基变量x大于0，而不是小于0的。因为相当于一个移项。

转轴，就相当于给这一行都除以这个非基变量。再给其他行做高斯消元。

注意，这个时候，第0行（答案行）的常数项是答案的相反数。

因为每一次转轴和高斯消元的过程，就变成了给答案减去一个数。

另外，我们注意到基变量的系数肯定为1，而非基变量只有n个，我们只要每行开n个空间，存下非基变量的系数就可以了。

id表示第i个非基变量存的是几号变量，id[n+i]表示第i行的基变量是几号变量。

uoj数据太恶心。97分过不了（其实没有人过得了

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
using namespace std;

int n,m,t;
double a[30][25];
double eps=1e-5;
int id[45];
double ans[25];

void pivot(int x,int y){
	swap(id[n+x],id[y]);
	double temp=a[x][y];
	for(int i=0;i<=n;i++) a[x][i]/=temp;
	a[x][y]=1/temp;
	for(int i=0;i<=m;i++) if(x!=i){
		temp=a[i][y];a[i][y]=0;
		for(int j=0;j<=n;j++) a[i][j]-=temp*a[x][j];
	}
}

bool prepare(){
	int x,y;
	while(1){
		x=y=0;
		for(int i=1;i<=m;i++) if(a[i][0]<-eps) {x=i;if(rand()%3!=0) break;}
		if(!x) break;
		for(int i=1;i<=n;i++) if(a[x][i]<-eps) {y=i;if(rand()%3!=0)break;}
		if(!y){
			printf("Infeasible");
			return false;
		}
		pivot(x,y);
	}
	return true;
}

bool simplex(){
	int x,y;
	double mmin;
	while(1){
		x=y=0;
		for(int i=1;i<=n;i++) if(a[0][i]>eps) {y=i;break;}
		if(!y) break;
		mmin=(double)1e18;
		for(int i=1;i<=m;i++) if(a[i][y]>eps && a[i][0]/a[i][y]<mmin) {x=i;mmin=a[i][0]/a[i][y];}
		if(!x) {
			printf("Unbounded");
			return false;
		}
		pivot(x,y);
	}
	return true;
}

int main(){
	srand(23333);
	scanf("%d %d %d",&n,&m,&t);
	for(int i=1;i<=n;i++) scanf("%lf",&a[0][i]);
	for(int i=1;i<=m;i++){
		for(int j=1;j<=n;j++) scanf("%lf",&a[i][j]);
		scanf("%lf",&a[i][0]);
	}
	for(int i=1;i<=n;i++) id[i]=i;
	if(prepare() && simplex()){
		printf("%.8lf\n",-a[0][0]);
		if(t){
			for(int i=1;i<=m;i++) if(id[n+i]>=1)ans[id[n+i]]=a[i][0];
			for(int i=1;i<=n;i++) printf("%.8lf ",ans[i]);
		}
	}
}

关于对偶:

前面我们研究的问题都是“约束为小于等于，求最大值的问题”，然而现在要求解得问题是"约束为大于等于，求最小值的问题"。

首先符号不是问题，我们只要将两边同时乘上-1，就可以变号了。

最小值也不是问题，那我们在单纯形算法的时候，在答案式拿出一个系数为负的就可以了。

但是这样使得在找初始解的时候可能会变慢许多，所以，有人可以证明上面的两个问题是一个对偶问题，也就是答案相同。

那么怎么个对偶法呢？

对于标准型线性规划问题：

$\\maximize\ c*x \\s.t. \ A_i*x<=b_i\ \ (i\in[1,m])$