快速掌握简单线性回归：从理论到实践

在统计学中，线性回归是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。当因变量和自变量之间高度相关时，我们就可以使用线性回归来对数据进行预测。

一个带有一个自变量的线性回归方程代表一条直线，为了方便理解，今天我们就拿只有一个自变量的线性回归方程来探讨简单线性回归。

今天，我们有三个目标：

使用Scikit-Learn完成一项简单线性回归任务；
理解简单线性回归的原理并推导其公式；
从零搭建我们的简单线性回归模型工具。

一、三分钟快速实现线性回归

sklearn库提供了大量机器学习模型的训练工具，包括各种各样的线性回归模型。今天我们用它来演示简单线性回归模型的使用。

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.cross_validation import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

# 导入糖尿病数据
diabetes = datasets.load_diabetes()

# 仅使用第三个特征
# sklearn接受的输入中，特征集是2维数据，
# 所以我们要增加一个维度，将长度为n的一维向量，变成n*1的二维向量
X = diabetes.data.copy()[:, np.newaxis, 2]
y = diabetes.target.copy()

# 将数据分为训练集和测试集
X_train = X[:-20]
X_test = X[-20:]
y_train = diabetes.target[:-20]
y_test = diabetes.target[-20:]
# sklearn提供了分割训练集与测试集的方法，不过这次为了让大家得到一致的结果，
# 我们直接取最后20个样本作为测试集（我们也可以设置train_test_split方法中
# 的random_state参数，用来保证每次实验的训练集和测试集是一致的。）
# X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.05)

# 创建线性回归模型对象
reg = linear_model.LinearRegression(fit_intercept=True)

# 训练模型
reg.fit(X_train, y_train)

# 预测测试数据
y_pred = reg.predict(X_test)

# 打印系数
print('coefficients: ', reg.coef_)
print('intercept: ', reg.intercept_)

# 打印均方误差
print('Mean squared error: ', mean_squared_error(y_test, y_pred))

# 打印R2分数
print('Variance score: ', r2_score(y_test, y_pred))

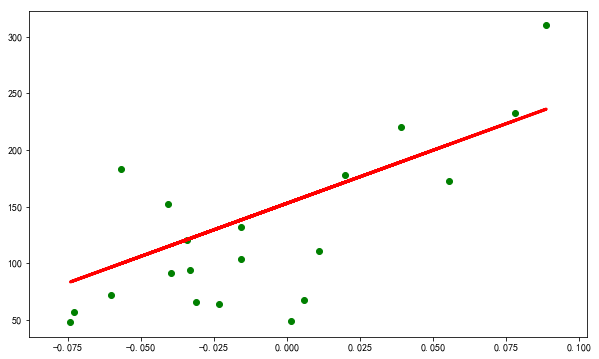
# 画图
plt.scatter(X_test, y_test, color='green')
plt.plot(X_test, y_pred, '-r', linewidth=3)
plt.show()

输出为：

coefficients:  [938.23786125]
intercept:  152.91886182616167
Mean squared error:  2548.0723987259703
Variance score:  0.47257544798227136

$R^2$ 分数仅有0.47，效果不是特别好，但是没关系，我们主要是以这个例子演示一下如何快速操作简单线性回归。

二、简单线性回归的原理

我们可能听过最小二乘法(OLS)这个词，它就是我们理解简单线性回归模型的关键。最小二乘法，其实就是最小化残差的平方和。

举个例子，有两组数：

x = [1, 3, 5]
y = [5, 6, 7]

现在我们要找到从x到y的映射关系，即如何对x中的3个数进行转换，近似得到y中的3个数。假设x和y之间存在这样的关系：

$\hat{y_i} = ax_i + b$

其中 $\hat{y}$ 是我们的y的预测值。很容易理解的一点是，我们的预测不可能总是那么完美，因此我们预测的数值与实际数值之间的差异，就是残差，即：

$error = y - \hat{y}$

我们的残差平方和，就是：

$RSS(SSE) = \sum_{i=1}^{n}{(y_i-\hat{y_i})^2} = \sum_{i=1}^{n}{[y_i-(ax_i+b)]^2}$

我们的目的是使得预测值尽可能地接近实际值，即残差越小越好。也就是说，当我们找到一组（a, b），使得残差平方和最小时，就说明在某种程度上，我们找到了预测效果最好的简单线性回归模型。

为什么要用残差的平方和，而不是残差呢？因为残差有正有负，他们的和不能代表真正的误差；那为什么不用残差的绝对值呢？其实残差的绝对值是一个很好的指标。但是对机器和数学来说，计算、表示残差的平方和时，远比计算和表示残差的绝对值要来得方便；同时，由于平方和的数据形态是一个U型的曲线，方便我们通过求导、随机梯度下降等方式得到最小值。

那么接下来我们就来求解我们的系数(a, b)，如前边所言，残差平方和的数据形态是一个U型曲线，因此当且仅当导数为0时，我们得到最低点。

1. 求解`b`

J(a, b)代表损失函数，在这个例子中，就是我们上边提到的残差平方和。先对b求导，并使导数等于0：

$\begin{aligned} &J(a,b) = \sum_{i=1}^{n}{[y_i-(ax_i+b)]^2}\\ &=> \frac{\partial{J(a,b)}}{\partial{b}}=\sum_{i=1}^{n}{2[y_i-(ax_i+b)](-1)}=0\\ &=> \sum_{i=1}^{n}{(y_i-ax_i-b)}=0\\ &=> \sum_{i=1}^{n}{y_i}-a\sum_{i=1}^{n}{x_i}-\sum_{i=1}^{n}{b}=0\\ &=> b=\frac{1}{n}\sum_{i=1}^{n}{y_i}-\frac{1}{n}a\sum_{i=1}^{n}{x_i}\\ &=> b=\overline{y}-a\overline{x} \end{aligned}$

2. 求解`a`

$\begin{aligned} &\frac{\partial{J(a,b)}}{\partial{a}}=\sum_{i=1}^{n}{2[y_i-(ax_i+b)](-x_i)}=0\\ &=>\sum_{i=1}^{n}{(y_ix_i-ax_i^2-bx_i)}=0\\ b=\overline{y}-a\overline{x}\quad&=>\quad\sum_{i=1}^{n}{(y_ix_i-ax_i^2-\overline{y}x_i+a\overline{x}x_i)}=0\\ &=>\sum_{i=1}^{n}{(y_ix_i-\overline{y}x_i)}-a\sum_{i=1}^{n}{(x_i^2-\overline{x}x_i)}=0\\ &=>a=\frac{\sum_{i=1}^{n}{(y_ix_i-\overline{y}x_i)}}{\sum_{i=1}^{n}{(x_i^2-\overline{x}x_i)}}\\ 又&\quad\sum_{i=1}^{n}x_i\overline{y}=n\overline{x}\overline{y},\quad\sum_{i=1}^{n}x_i\overline{x}=n\overline{x}^2\\ =>a&=\frac{\sum_{i=1}^{n}{(y_ix_i-\overline{y}x_i-\overline{x}y_i+\overline{x}\overline{y})}}{\sum_{i=1}^{n}{(x_i^2-\overline{x}x_i-\overline{x}x_i+\overline{x}^2)}}\\ &=\frac{\sum_{i=1}^{n}{(x_i-\overline{x})(y_i-\overline{y})}}{\sum_{i=1}^{n}{(x_i-\overline{x})^2}} \end{aligned}$

这两个推导过程，不熟悉的同学最好还是在草稿纸上演算一下，有不明白的地方可以留言沟通。

现在我们成功地推导出了(a, b)的求解公式，并且转换成了比较友好的形式，即：

$\begin{aligned} a&=\frac{\sum_{i=1}^{n}{(x_i-\overline{x})(y_i-\overline{y})}}{\sum_{i=1}^{n}{(x_i-\overline{x})^2}}\\ \quad\\ b&=\overline{y}-a\overline{x} \end{aligned}$

那么接下来，我们就尝试将求解公式实现一下。需要注意的是，如果所有的点分布在一条与x轴垂直的直线上，那对于所有点的横坐标，有 $x_i=\overline{x}$ ，则我们的求解公式是无解的，因为它的斜率是无限的。

三、从零搭建一个简单线性回归模型工具

import numpy as np
import matplotlib.pyplot as plt


class LinearRegression():
    def __init__(self):
        self.coef_ = 0
        self.intercept_ = 0
        self.X = None
        self.y = None
        self.y_pred = None
        self.sse = 0
        self.mse = 0
        self.rmse = 0
        self.mae = 0
        self.ssr = 0
        self.sst = 0
        self.r2 = 0

    def input_data(self, x, y):
        self.X = np.array(x)
        self.y = np.array(y)

    def solve(self):
        x = self.X
        y = self.y
        self.coef_ = sum((x - x.mean()) * (y - y.mean())) / sum((x - x.mean())**2)
        self.intercept_ = y.mean() - self.coef_ * x.mean()
        self.y_pred = np.array(x * self.coef_ + self.intercept_)

    def predict(self, x_new):
        return self.coef_ * x_new + self.intercept_

    def plot(self):
        plt.figure(figsize=(10, 6))
        plt.scatter(self.X, self.y, marker='+', color='green')
        plt.plot(self.X, self.y_pred, '-r')
        plt.text(1, 7.9, 'a:  {0:.2f}'.format(self.coef_), weight='bold', color='black', fontsize=16)
        plt.text(1, 7.7, 'b:  {0:.2f}'.format(self.intercept_), weight='bold', color='black', fontsize=16)
        plt.text(1, 7.5, 'R2: {0:.2f}'.format(self.r2), weight='bold', color='black', fontsize=16)
        plt.text(1, 7.3, 'MSE:  {0:.2f}'.format(self.mse), weight='bold', color='black', fontsize=16)
        plt.show()

    def evaluate(self):
        self.sse = sum((self.y - self.y_pred) ** 2)
        self.mse = sum((self.y - self.y_pred) ** 2) / len(self.X)
        self.rmse = np.sqrt(self.mse)
        self.mae = np.mean(np.abs(self.y - self.y_pred))
        self.ssr = sum((self.y_pred - np.mean(self.y)) ** 2)
        self.sst = sum((self.y - np.mean(self.y)) ** 2)
        self.r2 = self.ssr / self.sst

在这个类中，我们实现了数据输入、求解、预测、画图、模型评估的过程。关于模型评估，我们稍微说明一下：

SSE: 残差平方和， $SSE=\sum_{i=1}^{n}{(y_i-\hat{y_i})^2}$ ；
MSE: 均方差， $MSE=\frac{1}{n}\sum_{i=1}^{n}{(y_i-\hat{y_i})^2}$ ；
RMSE: 均方根， $RMSE=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{(y_i-\hat{y_i})^2}}$ ；
MAE: 平均绝对误差， $MAE=\frac{1}{n}\sum_{i=1}^{n}{|y_i-\hat{y_i}|}$ ；
SSR: Sum of squares of the regression， $MSE=\sum_{i=1}^{n}{(\hat{y_i}-\overline{y_i})^2}$ ；
SST: Total sum of squares， $MSE=\sum_{i=1}^{n}{(y_i-\overline{y_i})^2}$ ；
$R^2$ : 确定系数，取值范围[0,1]，取值越大，表明拟合效果越好。 $R^2=\frac{SSR}{SST}=1-\frac{SSE}{SST}$ 。

那么接下来，我们拿一组数据测试一下。

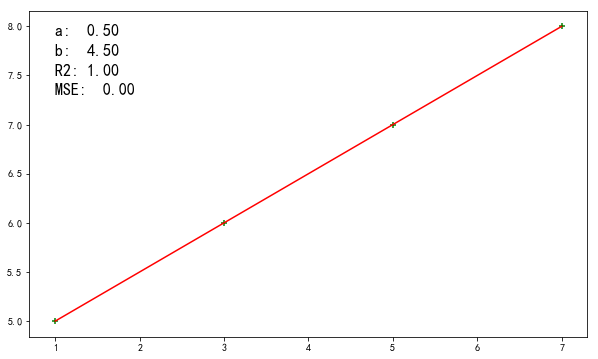
# 训练数据
X = np.array([1, 3, 5, 7])
y = np.array([5, 6, 7, 8])

# 创建模型
lr = LinearRegression()
lr.input_data(X, y)

# 求解
lr.solve()
lr.evaluate()

# 预测
x = 10
print('当X = 10时，y =', lr.predict(x))

# 画图
lr.plot()

输出为：

当X = 10时，y = 9.5

看来我们提供的数据太过完美，模型的预测和实际值完美重合。我们再加点料试试：

# 训练数据
X = np.array([1, 3, 5, 7, 4, 6, 8])
y = np.array([5, 6, 7, 8, 6, 8, 7])

# 创建模型
lr = LinearRegression()
lr.input_data(X, y)

# 求解
lr.solve()
lr.evaluate()

# 预测
x = 10
print('当X = 10时，y =', lr.predict(x))

# 画图
lr.plot()

输出为：

当X = 10时，y = 8.737704918032787

$R^2$ 为0.73，表现还可以哦。

好了，到现在为止，我们就成功地从零搭建了一个简单线性回归模型，大家有什么疑问吗？欢迎在下方留言！

我会经常为大家分享一些关于数据分析、数据挖掘、机器学习、爬虫等相关的原创内容，欢迎关注和转发！