冥想盆
【题目描述】
Mr.W 要制作一个体积为 Nπ 的 M 层生日蛋糕,每层都是一个圆柱体。 设从下往上数第 i 蛋糕是半径为 Ri,高度为 Hi 的圆柱。当 i<M时,要求 Ri>Ri+1且 Hi>Hi+1。由于要在蛋糕上抹奶油,为尽可能节约经费,我们希望蛋糕外表面(最下一层的下底面除外)的面积 Q最小。 令 Q =Sπ ,请编程对给出的 N 和 M ,找出蛋糕的制作方案(适当的 Ri 和 Hi 的值),使 S 最小。
(除 Q 外,以上所有数据皆为正整数)

【输入格式】
第一行为 N ,表示待制作的蛋糕的体积为 Nπ;
第二行为 M ,表示蛋糕的层数为 M 。
【输出格式】
输出仅一行,一个整数 S(若无解则 S=0 )。
【样例输入】
100
2【样例输出】
68【附:圆柱相关公式:】
体积
侧面积
底面积
【数据范围与提示】
对于全部数据,1≤N≤10^4,1≤M≤20。
首先分为四大部分:
1.感性理解深搜和剪枝
2.理解本题思路
3.着重理解代码的优化性
4.最后附上优秀的大佬博客
首先剪枝:
1.什么是“剪枝”
顾名思义,剪枝就是剪掉一下耗时的可以不要的东西,
举个形象的例子吧:一棵树,按照常理每一年都要剪掉一些枝条,为什么呢?因为要给主体部分留足够的营养,把这些浪费营养的枝条都剪掉,这就有了剪枝。同样的,在c++当中,剪枝就是为了把那些浪费时间,可以跳过枚举的给去掉,从而做到最快最简最优。
2.剪枝的三大原则
(1).正确性
这是最重要的,为什么呢?我们剪枝是为了代码的优化性,如果剪枝出现了错误,把该留下的全部删掉了,那么这个剪枝再怎么高级都没有用了。(正确性为剪枝的前提)
(2).准确性
可能会有疑问,准确和正确有怎么区别?正确是指剪掉的枝是该剪的,准确性就是为了优化代码而尽可能的剪去不能同行正解的枝条,剪枝有了较高的准确性之后才能更快更准更优。(准确性为剪枝的核心)
(3).高效性
高效指的就是:改善判断的准确性外,经常还需要提高判断操作本身的时间效率。但是你想一下,如果我们改善了剪枝判断的准确性,就不得不提高判断操作的复杂度,这也就同时降低了剪枝判断的时间效率。所以高效性就是我们剪枝最困难的一步,就是要解决这个矛盾,从而是代码变得高级。(高效性为剪枝的保障)
其次深搜的优化技巧
1.优化搜索顺序
我们在搜索当中,难免会出现一些树的各个层次、各个分支之间的顺序不是固定的,而且也会有不同的形态,这个坑坑洼洼就会影响我们的搜索,就想一条路,如果全都是坑,那么必然会影响我们奔跑的速度,所以我们就要优化搜索顺序,使这棵树的一些大层次可以是相似的,这样就可以大大的优化我们的搜索速度。(优化搜索顺序是技巧的前提,因为我们只有把路走直了,才可以进行更多的优化)
2.排除等效多余
这个就很好理解了,就是说如果我们在搜索的过程中,发现这棵树有好几个分枝都是等效的(相同的),那么这个时候我们就只需要对其中的一条分枝执行搜索。(排除等效多余是技巧的偷懒,这一步可以大大减少时间)
3.可行性剪枝
其实就是一个灵活性的问题,为什么这么说呢?因为如果我们在搜索的过程中,发现当前的这个分枝根本到不了我们递归的正规,也就是说走到了死胡同,这个时候就要立即折返绕路,而不是走到路的尽头发现是死胡同才返回。
某些题目条件的范围限制是一个区间,这时可行性剪枝也被称为“上下界剪枝”(可行性剪枝是技巧的核心,为什么呢?因为如果每一次都算到尽头那一定超时,所以这个就是核心)
4.最优性剪枝
这个就更加好理解了,就是说如果我们后面搜索到的比我们之前记录过的最小值还要大的话,就停止搜索,执行回溯。(最优性剪枝是技巧的保障,因为往往搜索到后面就会越来越麻烦,所以这个最优性可以让我们最快的确定最优解)
5.记忆化
记录每个状态的搜索结果,在重复遍历搜索的时候直接检索返回值。就好比我们在对图进行深搜的时候,标记一个节点是否已经被访问过。同时因为储存了状态,所以我们调用最优性剪枝的时候就会大大节省时间,这就是记忆化可以让一个原本没有记忆化是100多ms的代码变成一个10几ms的代码。(记忆化是技巧的高级,用好数组,灵活定义数组的初始状态)
最后来一个小小的总结吧
1.几乎所有的搜索都会用到可行性剪枝
2.在寻找极值的时候,优先考虑最优性剪枝和记忆化,因为没有最优化剪枝,十有八九都是超时的
3.部分搜索要回溯,其实就是我们自己调用一个值的时候要标记使用,然后用完之后要归零
4.有个小小的东西,dfs搜索的函数千万不要担心定义的数太多,往往在一开始的时候定义多一点也没关系,因为等你找到了正解之后可以进行技巧的修改,使得代码更加的简单快速,做到三大原则
接下来,理解本题的思路
不得不承认,我觉得最麻烦的就是这个半径和高的最小值,这个就要理解好题目。题目中说
半径如此,高也是如此
,,这意味着什么?意味着底下每一层的半径和高度至少比上一层多1,也就是说,最底下那一层的半径和高最小为m。
有了这一步,我们的半径和高的规律已经心中有数了,也知道应该怎样了,那么我们在主函数中的初始化应该是怎样的呢?
1.for(int i=m;i*i*m<=n;i++) //这个i表示的是半径的范围 2.for(int j=m;i*i*j<=n;j++) //这个j表示的是高的范围 3.if(i*i+2*i*j<minn) //这一步表示的是只有我们在枚举到这个表面积小于我们之前记录过的才可以继续 4.dfs(1,i*i*j,i*i+2*i*j,i,j) //进入递归函数, /* 1.从前1层开始 2.体积为i*i*j 3.表面积为2*i*j 4.i表示半径 5.j表示高 */万事开头难,慢慢理解题目就好了
我都以这个最慢的代码为基准,因为我最熟悉这个,然后其他的几个代码,把最慢的理解清楚之后,理解起来很简单,而且我都注释的很清楚了,所以不用慌。
接下来进入递归当中,递归当中最重要的莫过于剪枝了(我会放出三个代码,分别是最慢最好理解,次慢次理解,最快难理解),这三个代码剪枝的方法不一样,但始终是三个方面
1.前d层的体积加上后面体积的最小值还大于n(题目给出的体积的限制)就剪枝
2.前d层的体积加上后面体积的最大值还小于n,就剪枝
3.前d层的表面积加上后面的表面积大于我们记录过的最优解,剪枝(没有这一步,再多的剪枝都会超时,这个是最重要的剪枝也是最难的剪枝,而且最坑的是,就算你用数组来记录也没用,这是一条公式,一条极难想到的公式)
接下来我们一个一个理解啊
1.体积剪枝(最大值不足以满足题目要求) if(v+(r-1)*(r-1)*(h-1)*(m-d)<n)return; /* 1.如果当前体积加上之后每层的最大值,还比题目要求的体积小,直接结束该趟递归 2.我在主函数当中讲了我们的搜索是自下而上,所以下面一层的高和半径都比上面一层要大 3.为什么说是最大值呢?因为我们选取的是当前上一层的半径,而且越往上越小 而我们乘以的同样也是那么多层,所以说这个是最大值 */ 2.体积剪枝(最小值超过题目要求) if(v+m-d>n)return; /* 1.如果当前体积加上之后每层的最小值,还比题目要求的体积大,直接结束该趟递归 2.为什么说是最小值呢?因为我们的上一层的高和半径是比下面的那一层要小的,也就是最顶上的 可能半径就为1,是最小的,既然是最小的说明下面的就比他要大,但是我们就直接 最小半径的平方1*1*(m-d)也就是层数,那么可能会疑惑高去哪里了? 高也是假设了最小的1,所以整个半径平方乘以高乘以层数=1*1*1*(m-d)=m-d */ 3.最优性剪枝(剪掉超过最优解的) if(2*(n-v)/r+s>=minn)return; 不要着急这个我要慢慢给你们证明我们来感性证明一下最优性剪枝啊
首先我们分成几部分
第一部分:n-v
第二部分:minn
第三部分:除以r乘以2
第四部分:全部一起
第一部分:v
无论如何这个都是可以理解的,v代表前d层的体积,然后我们就是把这个蛋糕一层一层的体积相加就等于总体积
那么
这个就是剩下部分的体积,可以理解的吧
第二部分:minn
过了很久我终于又开始完善这个博客了。这个minn可能是比较难理解的,那么我们一步步来
这个的值是小于
为什么呢?因为这个r是我们记录的最开始的这个最底层的这个的半径,这个半径是所有半径当中最大的,所以每一次都这么计算的值是最大的,那么我们不难想到,既然原本是要小于的,只要这个值大于的话,是不是就可以剪枝?那么我们把这个式子所有的 r 提出来合并,就变成了
![(h[1]*r[1]+h[2]*r[2]+......+h[d]*r[d])*r](https://img-blog.csdnimg.cn/20181220133629341)
第三部分:除以r乘以2
这样看可能没有感觉,我们只看中间的那一串,h[1]*r[1]一直加到h[d]*r[d],然而我们的这个侧面积的公式就是2hd,所以我们就要进行一个小修改,变成
,这个就是我们之前辛辛苦苦记录过的前d层的表面积,也就是我们所更新过的minn值,就是到当前为止记录过的最小的表面积的值
第四部分:全部一起
好,我在上面说了如果我们找到的这个
大于
就要剪枝的对吧,那么我们也说了上面的小修改,我们先列出一个原不等式啊:
这个是我们的剪枝条件,但是因为这个的值就是我们之间已经找到了的v的值,所以我们直接用v来代替,然后剩下了就是 n-v=
是吧,这个时候我们就要把这个和之前我们修改过的放在一个,两边同时除以这个r乘以2就变成了
,这个是最终形式,s其实就是我们前d层的体积所对应的表面积,那么这个
是什么意思呢?就是说这个
这个是任何一个体积的共同形式,那么我们除以了r再乘以2之后就变成了什么呢,变成了
就是我们熟悉的侧面积,这个代表的是我们剩余体积的侧面积,加上我们之前的这个s就是全部的表面积,这个的计算结果是不能大于我们之前记录过的这个minn的值,所以的话,
这个就成为了我们最重要的剪枝了
所有的剪枝我都讲清楚了对吧,接下来就看代码实现吧
【代码实现1:最慢最好理解(自己打的):100多ms】
/*
题目解释:
题目的意思:有一个体积为Nπ的M层蛋糕,底下每一层的高度和半径至少比上一层的大1,
也就是说,最底下一次的半径和高度至少为M了。(关键关键)
求解符合题意,又要求其表面积要最小的蛋糕,求出其表面积最小值为多少。
依次递归用DPS去寻找符合体积大小的数据,求解找到的最小值便是答案
*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,minn=2e+9; //min表为面积最小的值,初始化为一个极大值
void dfs(int d,int v,int s,int r,int h)
//前d层蛋糕体积为v 表面积为s 第d层半径r 高度h
{
if(d==m)//前d层就是m层,表示我们已经搜索完了
{
if(v==n)minn=s;//如果体积也符合题目要求的话,更新表面积的最小值
return;//返回值
}
if(v+(r-1)*(r-1)*(h-1)*(m-d)<n)return;
/*
1.如果当前体积加上之后每层的最大值,还比题目要求的体积小,直接结束该趟递归
2.我在主函数当中讲了我们的搜索是自下而上,所以下面一层比上面一层要小
3.为什么说是最大值呢?因为我们选取的是当前上一层的半径,而且越往上越小
而我们乘以的同样也是那么多层,所以说这个是最大值
*/
if(v+m-d>n)return;
/*
1.如果当前体积加上之后每层的最小值,还比题目要求的体积大,直接结束该趟递归
2.为什么说是最小值呢?因为我们的上一层是比下面的那一层要小的,也就是最顶上的
可能半径就为1,是最小的,既然是最小的说明下面的就比他要大,但是我们就直接
最小半径的平方1*1*(m-d)也就是层数,那么可能会疑惑高去哪里了?
高也是假设了最小的1,所以整个半径平方乘以高乘以层数=1*1*1*(m-d)=m-d
*/
if(2*(n-v)/r+s>=minn)return;
/*
如果求解过程半途找到比当前最小值,也就是minn的值还大的数据,结束该趟递归
这一步是最关键的一步但是我不知道现在在这里怎么表示出来
*/
for(int i=r-1;i>=m-d;i--)
/*
i(半径)[再上一层的半径]的最小值要保证大于当前这一层半径的最小值
题目解释当中说的至少要大1,也就是说上一层的半径最大是当前这一层的半径-1
也就是r-1
最小的话就是也要大于等于剩下的层数,不然后面的层就没有整数半径
比如说:
总共有5层,当前是第3层(顺数),第3层的半径是5,
那么第2层的半径最大就是4,最小的话就是(5-3)=2
因为只有大于等于2的时候,这一层的上一层才有半径,
如果第2层的半径是1的话,那么至少要大于等于1,也就是第1层的半径小于等于0
这个显然是不可能的
*/
{
for(int j=h-1;j>=m-d;j--)
/*
j(高度)[再上一层的高度]的最小值要保证大于当前这一层高度的最小值
跟半径是同样的道理,这里就不再解释了
*/
{
if((i*i*j+v<=n)&&(s+2*i*j<minn))
/*如果我们后面找到的这个半径和高度组合的体积小于等于n*/
/*并且它的面积比我们之前记录过的要小的话*/
dfs(d+1,v+i*i*j,s+2*i*j,i,j);/*递归搜索子状态,也就是处理下一个*/
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=m;i*i*m<=n;i++)
/*
1.i表示半径,半径的平方(也就是底面积)*层数(也就是体积)
小于要求的体积的话,可以继续
2.i从m开始是因为,底下每一层的高度和半径至少比上一层的大1,
也就是说,最底下一次的半径和高度至少为M了
*/
{
for(int j=m;i*i*j<=n;j++)
/*
1.j表示高度,高度乘以底面积小于要求体积,可以继续
2.i从m开始是因为,底下每一层的高度和半径至少比上一层的大1,
也就是说,最底下一次的半径和高度至少为M了
*/
{
if(i*i+2*i*j<minn)/*小于我们一直更新的最小值,才传入*/
dfs(1,i*i*j,i*i+2*i*j,i,j);
/*
从第m层开始,我们之前的枚举是自下而上,所以在搜索中也是自下而上
注意:(分开五个来分析)
(1)从前1层开始
(2)体积是半径*半径*高
(3)表面积不单单是侧面积,最底下那一层的表面积
(4)i表示半径
(5)j表示高度
*/
}
}
printf("%d\n",minn);/*输出最小值*/
return 0;
}
/*
体积V=πR*R*H
侧面积A’=2*π*R*H
底面积A=π*R*R
*/这个代码为什么会最慢了,因为我们没有用数组,也就是说,没有我们之前的这个记忆化剪枝技巧
【代码实现2:次慢:30多ms】
#include<cstdio>
#include<cstring>
#include<algorithm>
#define oo 1000000000
using namespace std;
int ans;
int minn[20];//存储体积
int n,m;
void dfs(int k,int r,int h,int s,int v)
//k:当前层数 r:当前层的半径 h:高度 s:表面积 v:剩下的体积
{
if (s+2*v/r>ans) return;
//我们知道剩余的体积,能不能根据体积,估算一个剩余的侧面积,
//如果( 当前的表面积+余下的侧面积的最小值)
//比最优值还大,那么当前层的搜索就没有意义。
if (v-minn[m-k]<0) return;
//如果剩余的体积减去后面要用的体积小于0的话,说明不够体积做一个蛋糕
if (k==m)//边界情况
{
if(v==0) if(s<ans) ans=s;
return;
}
for(int tr=r-1;tr>=m-k;tr--)
for(int th=h-1;th>=m-k;th--)//不断缩小半径和高度 进行枚举(跟那个的意思是一样的)
{
int ts,tv;
ts=s+2*tr*th;//后面的表面积
tv=v-tr*tr*th;//剩下的体积
dfs(k+1,tr,th,ts,tv);//搜索下一个
}
}
int main()
{
scanf("%d%d",&n,&m);
ans=oo;
int j=1;//最小的高为只能为1
for(int i=1;i<=m;i++)//预处理一个数组将最小的存起来 等会剪枝
{
minn[i]+=i*i*j;//记录体积
j++;//高会增加,题目中说了
}
for(int r=m;r*r*m<=n;r++)//因为半径是越来越小的 所以r的大致范围可以确定
for(int h=n/(r*r);h>=m;h--)//高度的大致范围也可以确定
{
int s,v;//表面积和剩下的体积
s=r*r+2*r*h;//第一层的侧面积+总顶面积(可以通过平移使所有顶面积拼成第一层的顶面积)
v=n-r*r*h;
dfs(1,r,h,s,v);
}
if(ans==oo) ans=0;//不可能这么大,所以就是没有体积炸掉了
printf("%d\n",ans);
return 0;
}这个用了记忆化,但是仍然慢的主要原因应该是这个代码的很多表达方式不是最简单,让电脑运行次数最少最方便的
【代码实现3:最快:10多ms】
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,minv[21],mins[21];
//V=n*pi m 层数 自顶向下1.2.3...m
//minv[i]表示i层到0层加起来的最小总体积 minvs 最小表面积
const int inf=1000000000; // inf 足够大就可以 int(32) -2^31~2^31-1=2147483647
int best=inf; //best 最小表面积
void dfs(int depth,int sumv,int sums,int r,int h)//深度优先搜索 自底m向上搜索
//depth表示剩余层数r h表示当前层得半径和高度 sumv已经用的总体积 sums已经生成的总表面积
{
if(depth==0)
{
if(sumv==n&&sums<best)//搜索完成 更新最小表面积best
{
best=sums;
}
return;
}
// 三个剪枝条件:
//1、已经搜索过的体积加上还未搜索过的最小体积不能比总体积n 大
//2、已经搜索过的表面积加上还未搜索过的最小表面积不能比之前的最小总表面积best大
//3、n-sumv既所剩体积记作dv 还需要的表面积为s
//s=2*ri*hi+2*r(i-1)*h(i-1)+... >=2*ri*hi*ri/r+2*r(i-1)*h(i-1)*r(i-1)/r+...
// =2*dv/r(i从depth-1取,r为当前半径 ri/r<1)
// 所以得到还需要的最小表面积s=2*(n-sumv)/r,
//如果最小的s和已经搜索过的表面积sums依然比best大 就不用继续搜索了
if(sumv+minv[depth-1]>n||sums+mins[depth-1]>best)
//剪枝如上所述
return;
for( int i=r-1;i>=depth;i--)
//递减顺序枚举depth层半径的每一个可能值,这里第depth层的半径最小值为depth
{
if(depth==m)sums=i*i;
//俯视蛋糕底面积作为外表面积的初始值(总的上表面积,以后只需计算侧面积)
int maxh=min((n-sumv-minv[depth-1])/(i*i),h-1);
//maxh最大高度,即depth层蛋糕高度的上限,
//(n-sumv-minv[dep-1])表示第depth层最大的体积
for(int j=maxh;j>=depth;j--) //同理,第depth层的最小高度值为depth
{
dfs(depth-1,sumv+i*i*j,sums+2*i*j,i,j);//递归搜索子状态
}
}
}
int main()
{
scanf("%d%d",&n,&m);
int rmax=sqrt(n); //rmax初始半径 底层半径 最大值为sqrt(n)
int hmax=n; //hmax初始高度 高度最大为 n
minv[0]=mins[0]=0;
for(int i=1;i<=m;i++)//初始化minv和mins数组
{
minv[i]=minv[i-1]+i*i*i; //从顶层(即第1层)到第i层的最小体积
//minv[i]成立时第j层的半径和高度都为j
mins[i]=mins[i-1]+2*i*i;
}
dfs(m,0,0,rmax,hmax);
//dfs(m,0,0,n+1,n+1);
if(best==inf)best=0; //无解
if(best==0)printf("0\n");
else printf("%d\n",best);
return 0;
}最快的,用了记忆化,而且所有的表达方式也是为了后面更方便而定义的
最后放上几个大佬的博客,感谢这些大佬
博客1 博客2 博客3 博客4 博客5 博客6
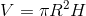
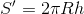
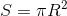
![n-v=n-(h[1]*r[1]*r[1]+h[2]*r[2]*r[2]+......+h[d]*r[d]*r[d])](https://img-blog.csdnimg.cn/20181220133629305)
![\frac{(h[1]*r[1]+h[2]*r[2]+......+h[d]*r[d])*r }{r}*2](https://img-blog.csdnimg.cn/20181220133629359)
![h[1]*r[1]*r[1]+h[2]*r[2]*r[2]+......+h[d]*r[d]*r[d]>](https://img-blog.csdnimg.cn/20181220133629411)