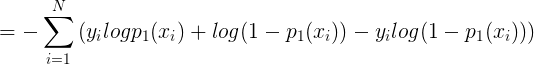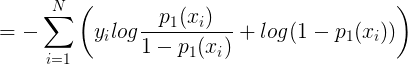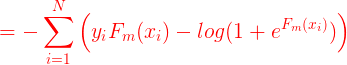上一篇文章讲了GBDT的回归篇,其实这一篇文章的原理的思想基本与回归相同,不同之处在于分类任务需用的损失函数一般为logloss、指数损失函数。
回顾下logistic regression有助于我们进一步的了解GBDT是如何进行分类的,线性模型是我们使用最简单的模型,但却蕴涵着机器学习中一些重要的基本思想,我们把线性回归模型简写为:
考虑二分类任务,其输出标记为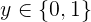
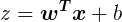
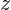
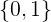
对数几率函数是一种“Sigmoid”函数,它将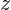
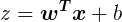
进行如下变换:
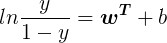
若将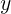
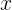
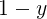
称为“几率(odds)”,反映了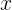
若将上式中的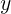
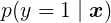
算出:
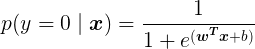
对于给定的样本集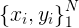

设: 
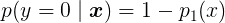
似然函数为:
对数似然函数为:
![\large L(w,b)=\sum _{i=1}^{N}\left [ y_ilogp_1(x_i)+(1-y_i)log(1-p_1(x_i)) \right ]](https://img-blog.csdnimg.cn/20181218152543289)
对上式求极限找到的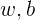
这里要求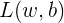
其中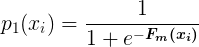
而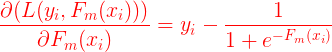
参考如下:只不过下面的推导是对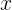






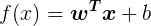
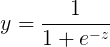
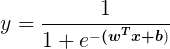
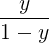
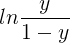
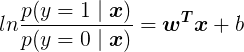

![\large \prod _{i=1}^{N}\left [ p_1(x_i) \right ]^{y_i}\left [ 1-p_1(x_i) \right ]^{1-y_i}](https://img-blog.csdnimg.cn/20181218152543267)
![\large L(y_i,F_m(x_i)))={\color{Red} -}\sum _{i=1}^{N}\left [ y_ilogp_1(x_i)+(1-y_i)log(1-p_1(x_i)) \right ]](https://img-blog.csdnimg.cn/20181218152543336)