一、学习目标
(1)了解连续模型及解题步骤。
(2)掌握用 dsolve 求解常见的微分方程解析解。
(3)掌握用 ODE 家族的求解器求解数值解。
(4)掌握使用专用的求解器求解。
二、连续模型介绍
连续模型是指模型是连续函数的一类模型总称,具体建模方法主要是微分方程建模。微分方程建模是数学建模的重要方法,因为许多实际问题的数学描述将导致求解微分方程的定解问题。把形形色色的实际问题化成微分方程的定解问题,大体上可以按以下几步:
1. 根据实际要求确定要研究的量(自变量、未知函数、必要的参数等)并确定坐标系。
2. 找出这些量所满足的基本规律(物理的、几何的、化学的或生物学的等等)。
3. 运用这些规律列出方程和定解条件。
MATLAB 在微分模型建模过程中的主要作用是求解微分方程的解析解, 将微分方程转化为一般的函数形式。 另外, 微分方程建模, 一定要做数值模拟, 即根据方程的表达形式, 给出变量间关系的图形, 做数值模拟也需要用 MATLAB 来实现。
微分方程的形式多样,微分方程的求解也是根据不同的形式采用不同的方法, 在建模比赛中, 常用的方法有三种:
1. 用 dsolve 求解常见的微分方程解析解
2. 用 ODE 家族的求解器求解数值解
3. 使用专用的求解器求解
三、实例演练
1. 常规微分方程的求解
微分方程在 MATLAB 中固定的表达方式, 这些基本的表达方式如下表所示:
对于通常的微分方程, 一般需要先求解析解, 那么 dsolve 是首先考虑的求解器,因为dsolve 能够求解解析解,其具体的用法如下:
| 函数名 | 函数功能 |
| Dy | 表示y关于自变量的一阶导数 |
| D2y | 表示y关于自变量的二阶导数 |
| dsolve('equ1','equ2',...) | 求微分方程的解析解,equ1、equ2、...为方程或条件 |
| simplify(s) | 对表达式s使用maple的化简规则进行化简 |
| [r, how]=simple(s) | simple 命令就是对表达式s用各种规则进行化简,然后用 r 返回最简形式,how 返回形成这种形式所用的规则 |
| [T, Y]=solver(odefun, tspan,y0) | 求微分方程的数值解,其中的 solver 为命令 ode45、ode23、ode113、ode15s、ode23s、ode23t、ode23tb之一,odefun是显式常微分方程,在积分区间 tspan=[t0, tf] 上,从 t0 到 tf,用初始条件y0求解,要获得问题在其他指定时间点t0,t1,t2,...上的解,则令tspan=[0,t1,t2,...tf](要求是单调的)。 |
| ezplot(x,y,tmin,tmax) | 符号函数的作图命令,x,y为关于参数 t 的符号函数,[tmin,tmax] 为 t 的取值范围 |
[实例] 求微分方程 xy'+y-e^x=0 在初始条件 y(1)=2e 下的特解,并画出解函数的图形.
求解本问题的 Matlab 程序为:
syms x y
y=dsolve('x*Dy+y-exp(x)=0','y(1)=2*exp(1)','x')
ezplot(y)微分方程的特解为:y=1/x*exp(x)+1/x*exp (1) (Matlab格式),即 y=(e+e^x)/x ,此函数的图形如图 1:
图 1

2. ODE 家族求解器
如果微分方程的解析形式求解不出来, 那么退而求其次的办法是求解数值解, 那么这个时候就需要用 ODE 家族的求解器求解微分方程的数值解啦。
因为没有一种算法可以有效地解决所有的 ODE 问题,为此,MATLAB 提供了多种求解器,对于不同的 ODE 问题,采用不同的 Solver。MATLAB 中常用的微分方程数值解的求解器及特点如下表所示。
| Solver 求解器 | ODE 类型 | 特点 | 说明 |
| ode45 | 非刚性 | 单步计算; 4、5阶 Runge-Kutta 方法; 累计截断误差达O(x^3). |
大部分场合首选 |
| ode23 | 非刚性 | 单步计算; 2、3阶 Runge-Kutta 方法; 累计截断误差达O(x^3) |
使用于精度较低的情形 |
| ode113 | 非刚性 | 多步法; Adams 算法; 高低精度均可到 10^(-3)--10^(-6) |
计算时间比 ode45 短 |
| ode23t | 适度刚性 | 采用梯形算法 | 适度刚性情形 |
| ode15s | 刚性 | 多步法; Gear's 反向数值微分; 精度中等 |
若 ode45 失效时,可尝试使用 |
| ode23s | 刚性 | 单步法; 2阶 Rosebrock 算法; 低精度 |
当精度较低时,计算时间比 ode15s 短 |
| ode23td | 刚性 | 梯形算法; 低精度 |
当精度较低时,计算时间比 ode15s 短 |
要特别提醒的是:ode23、ode45 是极其常用的用来求解非刚性标准形式一阶常微分方程(组)初值问题解的 Matlab 的常用程序,其中:
ode23 采用龙格-库塔2 阶算法,用3 阶公式作误差估计来调节步长,具有低等的精度.
ode45 则采用龙格-库塔4 阶算法,用5 阶公式作误差估计来调节步长,具有中等的精度.
[实例] 导弹追踪问题
设位于坐标原点的甲舰向位于 x 轴上点 A(1, 0) 处的乙舰发射导弹,导弹头始终对准乙舰。如果乙舰以最大的速度 v0 (是常数)沿平行于 y 轴的直线行驶,导弹的速度是 5*v0,求导弹运行的曲线方程,以及乙舰行驶多远时,导弹将它击中?
记导弹的速度为 w,乙舰的速率恒为 v0。设时刻 t 乙舰的坐标为 (X(t),Y(t)),导弹的坐标为 (x(t),y(t)) 。当零时刻,(X(0),Y(0))=(1,0),(x(0),y(0))=(0,0),建立微分方程模型:
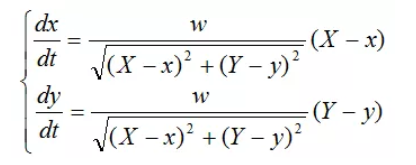
因乙舰以速度 v0 沿直线 x=1 运动,设 v0=1,w=5,X=1,Y=t,因此导弹运动轨迹的参数方程为

MATLAB 求解数值解程序如下:
(1) 定义方程的函数形式:
function dy=eq2(t,y)
dy=zeros(2,1);
dy(1)=5*(1-y(1))/sqrt((1-y(1))^2+(t-y(2))^2);
dy(2)=5*(t-y(2))/sqrt((1-y(1))^2+(t-y(2))^2);
end(2) 求解微分方程的数值解
t0=0,tf=0.21;
[t,y]=ode45('eq2',[t0 tf],[0 0]);
X=1;Y=0:0.001:0.21;plot(X,Y,'-')
plot(y(:,1),y(:,2),'*'),hold on
x=0:0.01:1; y=-5*(1-x).^(4/5)/8+5*(1-x).^(6/5)/12+5/24;
plot(x,y,'r')图 2

3.专用求解器
对于复杂的微分方程模型的求解, 可以借助 MATLAB 偏微分方程工具箱中的专用求解器。以下将以一个实例来看看如何借助偏微分方程工具箱来实现一个微分方程的求解与数值仿真。(具体见:https://www.mathworks.com/help/pde/ug/solve-problems-using-pdemodel-objects.html)
所研究的对象是一个二阶波的方程:
这个时候要查看一下 MALTAB 中哪个函数能求解相类似的方程,
图 3

solvepde 可以求解的方程形式为:
可以发现只要通过参数设定就可以将所要求解的方程转化成这种标准形式。
具体求解步骤如下:
%(1)设置参数
c=1;a=0;f=0;m=1;%方程的参数设置
%(2)定义波的空间位置
numberOfPDE=1;
model=createpde(numberOfPDE);%返回numberOfPDE个方程组的PDE模型对象。
geometryFromEdges(model,@squareg);%2-D边界,@squareg定义单位方形区域
pdegplot(model,'EdgeLabels','on');%绘制PDE几何图形,2-D
ylim([-1.1 1.1]);
axis equal
title 'Geometry With Lables Displayed';
xlabel x
ylabel y
%(3)定义微分方程模型的系数和边界条件
specifyCoefficients(model,'m',m,'d',0,'c',c,'a',a,'f',f);%Create the PDE coefficients.
applyBoundaryCondition(model,'dirichlet','Edge',[2,4],'u',0);
applyBoundaryCondition(model,'neumann','Edge',([1 3]),'g',0);
%(4)定义该问题的有限网格
generateMesh(model);
figure
pdemesh(model);
ylim([-1.1 1.1]);
axis equal
xlabel x
ylabel y

%(5)定义初始条件
u0=@(location)atan(cos(pi/2*location.x));
ut0=@(location)3*sin(pi*location.x).*exp(sin(pi/2*location.y));%ut0即Zu/Zt
setInitialConditions(model,u0,ut0);
%(6)方程的求解
n = 31; % 求解次数
tlist = linspace(0,5,n);
model.SolverOptions.ReportStatistics ='on';
result = solvepde(model,tlist);%for time-dependent problems,for all problems except for eigenvalue problems
u = result.NodalSolution;
%(7)模型的仿真
figure
umax = max(max(u));
umin = min(min(u));
for i = 1:n
pdeplot(model,'XYData',u(:,i),'ZData',u(:,i),'ZStyle','continuous', 'Mesh','off','XYGrid','on','ColorBar','off');
axis([-1 1 -1 1 umin umax]);
caxis([umin umax]);
xlabel x
ylabel y
zlabel u
M(i) = getframe;
end
