
1.1数据结构
·数据对象在计算机中的组织方式
逻辑结构
物理存储结构
·数据对象必定与一系列加在其上的操作相关联
·完成这些操作所用得方法就是算法
1.解决问题方法的效率跟数据的组织方式有关
例:书店找书
2.解决问题方法的效率跟空间的利用效率有关
例:PrintN( )函数
代码1:循环实现
#include<iostream>
using namespace std;
int main(){
void PrintN(int N);
PrintN(100000);
}
void PrintN(int N){
for(int i=1;i<=N;i++){
cout<<i<<endl;
}
}
代码2:递归实现
#include<iostream>
using namespace std;
int main(){
void PrintN(int N);
PrintN(100000);
}
void PrintN(int N){
for(int i=1;i<=N;i++){
cout<<i<<endl;
}
}
3.解决问题方法的效率跟算法的巧妙程度有关
例:写程序计算给定多项式在x点的值 ![]()
代码1:死算
double f (int n,double a[],double x){
int i;
double p = a[0];
for (i=1;i<=n;i++)
p+=(a[i]* pow(x,i));
return p;
}代码2:秦九韶算法 ![]()
double f (int n,double a[],double x){
double p=a[n];
for(i=n;i>0;i--)
p=a[i-1]+x*p;
return p;
}clock( ):捕捉从程序开始运行到clock( )被调用时所耗费的时间。这个时间单位是clock tick,即“时钟打点”。常数CLK_TCK:机器时钟每秒所走的时钟打点数,不同的机器可能不同。二者配合就能得到一个函数跑了多少秒。
一个常用模板:
#include<iostream>
#include<time.h>
clock_t start,stop;
//clock_t是clock()函数返回的变量类型
double duration;
//记录被测函数运行的时间,以秒为单位
using namespace std;
int main(){
//不在测试范围内的准备工作写在clock()调用之前
start=clock();//开始计时
MyFunction();//被测函数放在这里
stop=clock();//停止计时
duration=((double)(stop-start))/CLK_TCK; //得到以秒为单位的时间
//其他不在测试范围内的处理写在后面,例如输出duration的值
return 0;
}但是有时候函数跑得太快,不到一个tick,得出的duration为0。让被测函数重复运行充分多次,使得测出的总的时钟打点间隔充分长,最后计算被测函数平均每次运行的时间即可。添加
#define MAXK 1e7//被测函数最大重复调用次数
抽象数据类型(Abstract Data Type)
数据类型
数据对象集
数据集合相关联的操作集
抽象:描述数据类型的方法不依赖于具体实现
与存放数据的机器无关
与数据存储的物理结构无关
与实现操作的算法和编程语言均无关
是描述数据对象集合相关操作集“是什么”,并不涉及“如何做到”的问题
1.2算法(Algorithm)
定义:
1.一个有限的指令集
2.接受一些输入(有些情况下不需要输入)
3.产生输出
4.一定在有限步骤后终止
5.每一条指令必须:
有充分明确的目标,不可以有歧义
计算机能处理的范围之内
描述应不依赖于任何一种计算机语言以及具体实现手段
例1:选择排序算法的伪码描述
void SelectionSort ( int List[ ] , int N ){
for ( i = 0 ; i < N ; i++){
MinPosition = ScanForMin ( List , i , N-1);
//从List[i]到List[N-1]中找最小元
Swap ( List[i],List[MinPosition]);
//将未排序部分最小元换到有序部分最后的位置
}
}抽象——
List可以是数组也可以是链表
Swap可以用函数或者宏实现
衡量算法的指标
空间复杂度
时间复杂度:平时最关心的是最坏情况复杂度。
复杂度的渐进表示法


1.3应用实例:最大子列和问题
![]()
算法1 死算
int MaxSubseqSum1(int A[],int N){
int ThisSum,MaxSum=0;
int i,j,k;
for(int i=0;i<N;i++){ //i是子列左端位置
for(int j=i;j<N;j++){ //j是子列右端位置
ThisSum=0; //ThisSum是从A[i]到A[j]的子列和
for(k=i;k<=j;k++)
ThisSum+=A[k];
if(ThisSum>MaxSum) //如果刚得到的子列和更大
MaxSum=ThisSUm; //则更新结果
}
}
return MaxSum;
}算法2 改良的死算
int MaxSubseqSum1(int A[],int N){
int ThisSum,MaxSum=0;
int i,j;
for(int i=0;i<N;i++){ //i是子列左端位置
ThisSum=0; //ThisSum是从A[i]到A[j]的子列和
for(j=i;j<N;j++){ //j是子列右端位置
ThisSum+=A[k];//对于相同的i不同的j,只需在j-1次循环基础上累加一项即可
if(ThisSum>MaxSum) //如果刚得到的子列和更大
MaxSum=ThisSUm; //则更新结果
}
}
return MaxSum;
}算法3 分而治之
把一个大的问题分割成小块分别解决,最后再把结果合并起来

蓝色长条表示一个数组。第一步:分。把数组从中间一分为二,然后递归地去解决左右两边的问题。递归地去解决左边的问题可以得到左边的最大子列和。右边同理。最后算出跨越边界的最大子列和,找出这三个比较。
一个具体的例子:
第一步:分,分,分......分到不好再分。红色为第一级,橙色为第二级,黄色为第三极。
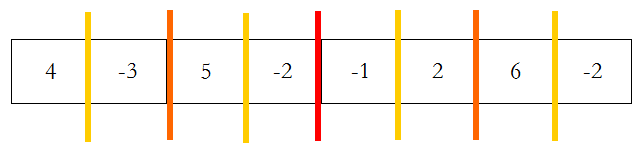
第二步:黄线左边最大子列和为4,返回4;右边为-3,返回0;边界分别往左和往右扫描,最大也为4。所以黄色部分(橙色部分的左半边)最大子列和为4。

第三步:所以橙线左边返回结果4,右边同理返回5。边界往左(-3、4)扫描,最大为1,往右(5、-2)扫描最大为5,所以跨越中线的最大子列和为6。整个橙色部分(红色部分的左半边)最大子列和为6。

第四步:红色左半边最大6;右半边最大8;中线往左扫描最大4,往右扫描最大7,所以跨越中线的最大子列和为11。所以最大子列和为11。

算法复杂度分析:假设整个问题里有N个数字,如果复杂度记作T(N)的话,那么则得到半边数字的时间复杂度为T(N/2),因为规模减半了。另一边同理。跨中线的子列和是往左扫描往右扫描,每个元素都被扫描了一遍,得到的复杂度应该是N的一个常数倍O(N)。由此得到递推公式:
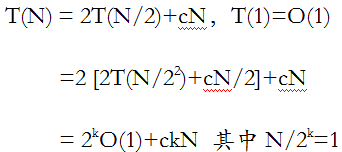

int Max3( int A, int B, int C ){ /* 返回3个整数中的最大值 */
return A > B ? A > C ? A : C : B > C ? B : C;
}
int DivideAndConquer( int List[], int left, int right ){
/* 分治法求List[left]到List[right]的最大子列和 */
int MaxLeftSum, MaxRightSum; /* 存放左右子问题的解 */
int MaxLeftBorderSum, MaxRightBorderSum; /*存放跨分界线的结果*/
int LeftBorderSum, RightBorderSum;
int center, i;
if( left == right ) /* 递归的终止条件,子列只有1个数字 */
{
if( List[left] > 0 ) return List[left];
else return 0;
}
/* 下面是"分"的过程 */
center = ( left + right ) / 2; /* 找到中分点 */
/* 递归求得两边子列的最大和 */
MaxLeftSum = DivideAndConquer( List, left, center );
MaxRightSum = DivideAndConquer( List, center+1, right );
/* 下面求跨分界线的最大子列和 */
MaxLeftBorderSum = 0; LeftBorderSum = 0;
for( i=center; i>=left; i-- ) /* 从中线向左扫描 */
{
LeftBorderSum += List[i];
if( LeftBorderSum > MaxLeftBorderSum )
MaxLeftBorderSum = LeftBorderSum;
} /* 左边扫描结束 */
MaxRightBorderSum = 0; RightBorderSum = 0;
for( i=center+1; i<=right; i++ ) /* 从中线向右扫描 */
{
RightBorderSum += List[i];
if( RightBorderSum > MaxRightBorderSum )
MaxRightBorderSum = RightBorderSum;
} /* 右边扫描结束 */
/* 下面返回"治"的结果 */
return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}
/*此函数用于保持接口相同,算法3参考老师的代码*/
int MaxSubseqSum3( int List[], int N )
{ /* 保持与前2种算法相同的函数接口 */
return DivideAndConquer( List, 0, N-1 );
}
(代码由MOOC网友“Ss蓝风sS ”于10月28日提交于https://www.icourse163.org/learn/ZJU-93001?tid=1003013004#/learn/content?type=detail&id=1004242196&cid=1005239402)算法4:在线处理
“在线”的意思是指每输入一个数据就进行即时处理,在任何一个地方中止输入,算法都能正确给出当前的解。
int MaxSubseqSum4( int A[], int N )
{ int ThisSum, MaxSum;
int i;
ThisSum = MaxSum = 0;
for( i = 0; i < N; i++ ) {
ThisSum += A[i]; /* 向右累加 */
if( ThisSum > MaxSum )
MaxSum = ThisSum; /* 发现更大和则更新当前结果 */
else if( ThisSum < 0 ) /* 如果当前子列和为负 */
ThisSum = 0; /* 则不可能使后面的部分和增大,抛弃之 */
}
return MaxSum;
}T(N)=O(N)

