一、算法原理
线性回归作为监督学习中经典的回归模型之一。
1.模型定义
线性回归需要学习得到的是一个映射关系 ,即当给定新的待预测样本时,我们可以通过这个映射关系得到一个测试样
本的预测值
。
例如当特征向量中只有一个特征时,需要学习到的函数应该是一个一元线性函数
。
当情况复杂时,考虑 存在n个特征的情形下,我们往往需要得到更多地系数。我们将
到
的映射函数记作函数
:
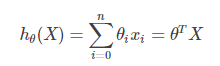
其中,为了在映射函数中保留常数项,令
为1,所以特征向量
,特征系数向量
。
2.损失函数
在需要通过学习得到的映射函数 中,需要通过训练集得到特征系数向量
,让真实值与预测值的差值最小。根据特征向量系数
,可有损失函数
如下 :
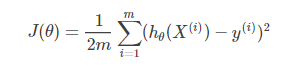
其中为需要学习到的函数,
为训练集样本的个数,
表示训练集中第
个样本的特征向量,
表示第
个样本中的标签。
可以从统计理论的角度出发来推导损失函数,可参考https://blog.csdn.net/jshazhang/article/details/80487825。
3.参数估计
损失函数只是一种策略,有了策略我们还要用适合的算法进行求解。在线性回归模型中,求解损失函数就是求与自变量相对应的各个回归系数和截距。有了这些参数,我们才能实现模型的预测(输入x,给出y)。
对于误差平方和损失函数的求解方法有很多,典型的如最小二乘法,梯度下降等。下面我们分别用这两种方法来进行求解。
(1)最小二乘法
最小二乘法可以将误差方程转化为有确定解的代数方程组(其方程式数目正好等于未知数的个数),从而可求解出这些未知参数。这个有确定解的代数方程组称为最小二乘法估计的正规方程。
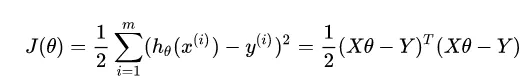

令上面得到的公式等于0,即可得到最终的求解:

(2)梯度下降法
梯度下降是另一种常用的方法,可以用来求解凸优化问题。它的原理有别于最小二乘法,它是通过一步步迭代(与最小二乘法的区别在后面介绍)求解,不断逼近正确结果,直到与真实值之差小于一个阈值,从而得到最小化损失函数的模型参数值的。它的公式如下:
![]()
我们不会将公式等于0来求极值,而是带入上面梯度下面公式来迭代完成求解,以下是梯度下降矩阵形式的最终求解结果:
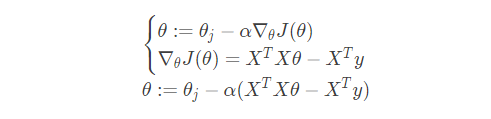
最小二乘法 vs 梯度下降法:
最小二乘法:
- 得到的是全局最优解,因为一步到位,直接求极值,因而步骤简单
- 线性回归的模型假设,这是最小二乘方法的优越性前提,否则不能推出最小二乘是最佳(即方差最小)的无偏估计
梯度下降法:
- 得到的是局部最优解,因为是一步步迭代的,而非直接求得极值
- 既可以用于线性模型,也可以用于非线性模型,没有特殊的限制和假设条件
4.正则化
当我们的损失函数 J(θ)在样本中损失较大时,会出现欠拟合的情况,即对样本的预测值和样本的实际结果值由较大的差距。
当我们的损失函数 J(θ) 在样本中损失约等于0 时,这时 hθ(X)图像穿过样本的每一个点,这样会出现过拟合的情况,缺乏泛化能力,函数波动比较大,对待预测的样本预测能力比较弱。
过拟合解决方法:(1):丢弃一些对我们最终预测结果影响不大的特征,具体哪些特征需要丢弃可以通过PCA算法来实现;(2):使用正则化技术,保留所有特征,但是减少特征前面的参数θ的大小,具体就是修改线性回归中的损失函数形式即可,岭回归以及Lasso回归就是这么做的。
无正则化时的损失函数:
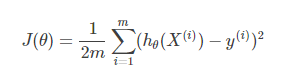
L1正则化下的损失函数:
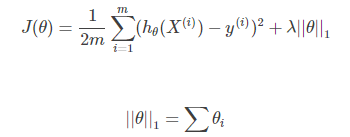
L2正则化下的损失函数:

L1正则化、L2正则化也称为Lasso正则化(Lasso回归)、岭正则化(岭回归),其中 λ为模型的超参数。岭回归与Lasso回归的出现不仅解决线性回归出现的过拟合问题,还可以解决通过正规方程方法求解θ的过程中出现的x转置乘以x不可逆的问题。
5.回归评价指标
回归算法的评价指标是MSE,RMSE,MAE、R-Squared。
(1)均方误差(MSE)(Mean Squared Error)

(2)均方根误差(RMSE)(Root Mean Squard Error)

(3)平均绝对误差(MAE)

(4)R方(R Squared)
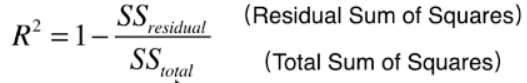
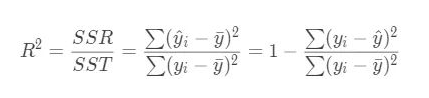
公式变形:

结论:
- R2 <= 1
- R2越大越好,当自己的预测模型不犯任何错误时:R2 = 1
- 当我们的模型等于基准模型时:R2 = 0
- 如果R2 < 0,说明学习到的模型还不如基准模型。 # 注:很可能数据不存在任何线性关系
二、算法实践
1.最小二乘实现和梯度下降实现
使用sklearn.datasets.load_boston即可加载相关数据。该数据集是一个回归问题。每个类的观察值数量是均等的,共有 506 个观察,13 个输入变量和1个输出变量。每条数据包含房屋以及房屋周围的详细信息。其中包含城镇犯罪率,一氧化氮浓度,住宅平均房间数,到中心区域的加权距离以及自住房平均房价等等。通过最小二乘和梯度下降法分别实现线性回归,在波士顿房价数据集上进行两种模型的对比。在梯度下降法中需要人为的设定学习率和迭代步数,一开始学习率设置较大,导致损失越来越大,通过多次试验最终确定了学习率和迭代步数。
#Author zsl
import numpy as np
import pandas as pd
from pandas import Series,DataFrame
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
def create_data():
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['MEDV'] = boston.target
df.columns = ['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT','MEDV']
data = np.array(df)
return data[:,:-1],data[:,-1]
class LeastSquared(object):
def __init__(self):
self.xArr = []
self.yArr = []
self.params = []
def fit(self,xArr,yArr):
self.xArr = xArr
self.yArr = yArr
xMat = np.mat(xArr)
yMat = np.mat(yArr).T
xTx = xMat.T*xMat
if np.linalg.det(xTx) == 0.0:
print('矩阵为奇异矩阵')
params = xTx.I*(xMat.T*yMat)
self.params = params
def predict(self,x_new):
y_predict = x_new*self.params
return y_predict
class GradientDescent(object):
def __init__(self, max_iter, learning_rate):
self.max_iter = max_iter
self.learning_rate = learning_rate
self.theta = []
self.cost = []
def fit(self, X, y):
self.cost = np.zeros(self.max_iter)
m,n = np.shape(X)
# a = np.ones((m,1),dtype=np.float)# 将x0 置为1 便于写成向量的乘积 theta*X
# X = np.column_stack((a,X))
self.theta = np.zeros((np.size(X[0,:])),dtype=float)
for iter_ in range(self.max_iter):
hypothesis = np.dot(X,self.theta)
loss = (hypothesis-y)
gradient = np.dot(X.T,loss)/m
self.theta = self.theta- self.learning_rate * gradient
self.cost[iter_] = 1.0/2*m*np.sum(np.square(np.dot(X,np.transpose(self.theta))-y))
#print ("cost: %f"%self.cost[iter_])
def predict(self,x_new):
result = np.dot(x_new,self.theta)
y_predict= result.reshape((x_new.shape[0],1))
return y_predict
def r2_score(y_test,y_predict):
n = len(y_test)
yArr = y_test
y_hat = y_predict
# ssr
diff_yhat = y_predict - np.mean(yArr)
ssr = np.sum(np.power(diff_yhat,2))
# sst
diff_y = yArr - np.mean(yArr)
sst = np.sum(np.power(diff_y,2))
return round(ssr/sst,2)
if __name__ == '__main__':
X,y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
ls = LeastSquared()
ls.fit(X_train, y_train)
ls_pre = ls.predict(X_test)
ls_r2 = r2_score(y_test, ls_pre)
print("ls_r2:",ls_r2) #ls_r2: 0.96
gd = GradientDescent(max_iter=5000, learning_rate=1e-6)
gd.fit(X_train, y_train)
gd_pre = gd.predict(X_test)
gd_r2 = r2_score(y_test, gd_pre)
print("gd_r2:",gd_r2) #gd_r2: 0.49
#绘制训练损失函数曲线和方法对比
fig, ax = plt.subplots(1,2,figsize=(16,12))
ax[0].set_xlabel('iterations')
ax[0].set_ylabel('cost')
ax[0].set_title('GradientDescent')
ax[0].plot(gd.cost,'r')
ax[1].plot(y_test,label='True')
ax[1].plot(ls_pre,label='LS')
ax[1].plot(gd_pre,label='GD')
plt.legend()
plt.show()
2.sklearn实现
官方英文文档地址:https://scikit-learn.org/stable/modules/classes.html#module-sklearn.linear_model
我们先从sklearn中导出普通线性模型、岭回归模型、lasso模型和sgdr模型四种模型,同时在波士顿房价数据集上进行四种模型的对比。比较了MAE、MSE和R2指标。存在问题是SGDR的结果不正确,未找到原因,后续解决。
#Author zsl
import numpy as np
import pandas as pd
from pandas import Series,DataFrame
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
#机器学习的普通线性模型、岭回归模型、lasso模型
from sklearn.linear_model import LinearRegression,Ridge,Lasso,SGDRegressor
#模型效果评估
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error
#导入机器学习相关的数据集
from sklearn.datasets import load_boston
def create_data():
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['MEDV'] = boston.target
df.columns = ['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT','MEDV']
data = np.array(df)
return data[:,:-1],data[:,-1]
if __name__ =='__main__':
X,y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
#普通线性回归模型
line = LinearRegression()
line.fit(X_train,y_train)
line_y_pre = line.predict(X_test)
line_score = line.score(X_test,y_test) #score 即为R2的结果
line_r2 = r2_score(y_test, line_y_pre)
print("line_score:",line_score,"line_r2:",line_r2)
line_mse = mean_squared_error(y_test, line_y_pre)
line_mae = mean_absolute_error(y_test, line_y_pre)
print("line_mse:",line_mse,"line_mae:",line_mae)
#岭回归模型
ridge = Ridge()
ridge.fit(X_train,y_train)
ridge_y_pre=ridge.predict(X_test)
ridge_r2 = r2_score(y_test, ridge_y_pre)
print("ridge_r2:",ridge_r2)
ridge_mse = mean_squared_error(y_test, ridge_y_pre)
ridge_mae = mean_absolute_error(y_test, ridge_y_pre)
print("ridge_mse:",ridge_mse,"ridge_mae:",ridge_mae)
#lasso模型
lasso = Lasso()
lasso.fit(X_train,y_train)
lasso_y_pre=lasso.predict(X_test)
lasso_r2 = r2_score(y_test, lasso_y_pre)
print("lasso_r2:",lasso_r2)
lasso_mse = mean_squared_error(y_test, lasso_y_pre)
lasso_mae = mean_absolute_error(y_test, lasso_y_pre)
print("lasso_mse:",lasso_mse,"lasso_mae:",lasso_mae)
#SGD模型
sgdr = SGDRegressor()#使用默认的学习率和迭代步数
sgdr.fit(X_train,y_train)
sgdr_y_pre = sgdr.predict(X_test)
sgdr_r2 = r2_score(y_test, sgdr_y_pre)
print("sgdr_r2:",sgdr_r2)
sgdr_mse = mean_squared_error(y_test, sgdr_y_pre)
sgdr_mae = mean_absolute_error(y_test, sgdr_y_pre)
print("sgdr_mse:",sgdr_mse,"sgdr_mae:",sgdr_mae)
#绘制三种方法的拟合曲线
plt.plot(y_test,label='True')
plt.plot(line_y_pre,label='Line')
plt.plot(ridge_y_pre,label='Ridge')
plt.plot(lasso_y_pre,label='Lasso')
plt.legend()
plt.show()
三种模型预测值及真实值的对比图:

三、算法总结
优点:
- 结果易于理解
- 计算简单
缺点:
- 对非线性数据拟合不好。
适用数据类型:
- 数值型和标称型数据。
算法类型:
- 回归算法
四、面试题
1.线性回归与逻辑回归的区别?
1)线性回归要求变量服从正态分布,logistic回归对变量分布没有要求。
2)线性回归要求因变量是连续性数值变量,而logistic回归要求因变量是分类型变量。
3)线性回归要求自变量和因变量呈线性关系,而logistic回归不要求自变量和因变量呈线性关系
4)logistic回归是分析因变量取某个值的概率与自变量的关系,而线性回归是直接分析因变量与自变量的关系
2.过拟合产生原因和解决方法?
产生的原因:
(1)因为参数太多,会导致我们的模型复杂度上升,容易过拟合
(2)权值学习迭代次数足够多(Overtraining),拟合了训练数据中的噪声和训练样例中没有代表性的特征.
解决方法:
- 交叉验证法
- 减少特征
- 正则化
- 权值衰减
- 验证数据
3.L1和L2正则的区别,如何选择L1和L2正则?
他们都是可以防止过拟合,降低模型复杂度。
L1会趋向于产生少量的特征,而其他的特征都是0,而L2会选择更多的特征,这些特征都会接近于0。L1在特征选择时候非常有用,而L2就只是一种规则化而已。
- L1是在loss function后面加上 模型参数的1范数(也就是|xi|)
- L2是在loss function后面加上 模型参数的2范数(也就是sigma(xi^2)),注意L2范数的定义是sqrt(sigma(xi^2)),在正则项上没有添加sqrt根号是为了更加容易优化
- L1 会产生稀疏的特征
- L2 会产生更多地特征但是都会接近于0