Why Most Decisions Are Easy in Tetris—And Perhaps in Other Sequential Decision Problems, As Well

读到一半觉得此文价值不大，后一半翻译较粗略。本文介绍了通过优势计算去除明显不好的动作选项的方法，这在工程应用上算是实用方法，但是几乎无法获得最好的结果。

题目：为什么大部分决策在俄罗斯方块中都很容易——也许在其他序贯决策问题中也是如此

摘要

我们检查了俄罗斯方块游戏中遇到的决策问题的顺序，发现大多数问题在下面的情境都很容易：不需要知道在游戏中得分良好的评价函数，就能在可选的操作中做出选择。这是游戏中普遍存在的三个条件带来的后果：简单优势，累积优势和非补偿性。可以利用这些条件来开发更快更有效的学习算法。此外，它们允许将某些类型的领域知识轻松地整合到学习算法中。在我们讨论的连续决策问题中，俄罗斯方块的这些属性不应该是独特的或罕见的。

1. 简介

人类遇到的许多问题本质上都是连续的，成功的结果不是取决于单一的决定，而是取决于一系列相关的决定。此外，通常对决策的后果存在不确定性。这些类型的问题，即不确定性下的顺序决策问题，尽管在Go等游戏（Silver等，2016）等大型复杂领域得到成功应用，但对于机器学习仍然具有挑战性。

开发更快更有效的学习算法的一种方法是研究遇到序贯决策问题的自然环境。众所周知，自然界的许多方面都具有规律性。例如，在自然界中观察到的网络与随机网络非常不同。它们表现出同质性（连接节点具有相关属性的趋势），并且它们倾向于具有非常高程度的一些节点。这两个属性已经预示了可以比搜索随机网络更有效地搜索自然网络的算法（Kleinberg，2000; Watts等，2002; Adamic等，2001;Säimsek＆Jensen， 2008）。自然序贯决策环境可能同样表现出规律性，可以为学习算法的发展提供信息。

我们深入研究了一个特定的环境：俄罗斯方块，这是有史以来最知名和最受欢迎的视频游戏之一。我们的兴趣不在于俄罗斯方块本身，而在于将其用作识别序贯决策环境中规律性的平台。

我们发现在玩俄罗斯方块时遇到的大多数个体问题在以下情境很容易：可以在可用的操作中做出选择，而不知道在游戏中得分良好的评价函数。此外，还有一个直观的特性，通常可以在不消除最佳操作的情况下消除大量操作。根本原因是域中的三种规则，我们将在以下部分中详细解释。

我们的分析是由关于单次问题的决策文献中的早期结果所推动的。在以下部分中，我们将回顾这些文献并描述我们在俄罗斯方块中的结果。我们的分析为进一步研究提出了两个直接的问题。首先是俄罗斯方块具有的这些规律是不是独特的或者罕见的。其次是如何利用这些规律来更快更有效地学习。我们将详细讨论这两个问题，并展示在双路棋上应用的结果。

2.背景

请考虑以下判断问题：为您提供了许多对象，并要求您确定哪个对象在指定（未观察到）的条件上具有最高值。例如，考虑到每种股票的许多特征（例如，行业类型和过去12个月的退货率），您可能会获得一些股票并要求确定哪些股票在五年内具有更高的回报率。这个问题叫做比较。

如果特征和标准之间的关系是线性的，则有三个条件可以使比较问题变得容易。当这些条件成立时，可以在不知道特征与标准之间的确切线性关系的情况下正确决策。仅知道权重的符号就足够了，并且在两个条件中，也知道权重减少的顺序。这些条件是简单优势（Hogarth＆Karelaia，2006），累积优势（Baucells等，2008）和非补偿性（Martignon＆Hoffrage，2002; Katsikopoulos，2011;Säimsek，2013）。

发现这些条件在大量的自然数据集中很普遍（Säimsek，2013）。在本研究中检查的51个数据集中，平均而言，简单优势保持在16％，累积优势保持在62％，并且对象之间的配对比较中的非补偿性保持在85％。此外，原则上，概率近似对于优势，简单优势和累积优势的普遍性大幅增加。

下面我们解释这三个条件并给出一个简单的示例。令 $y = w_0 + w_1 x_1 + w_2 x_2 +\dots + w_k x_k$ 表示特征与标准之间的线性关系，其中 $y$ 是标准， $w_0$ 是截距， $w_1,\dots, w_k$ 是权重， $x_1,\cdots ,x_k$ 是特征值。令 $x^A_i$ 表示对象 $A$ 的第 $i$ 个特征的值。为了便于说明而不失一般性，我们假设所有权重都是正的，并且权重按递减幅度排序。

2.1 简单优势

如果 $x^A_i\geq x^B_i, \forall i\textup{ and } \exists i \textup{ such that } x^A_i> x^B_i$ ，对象 A 优于对象 B 。如果对象 A 优于对象 B，则可以确定 A 具有更高的标准值。我们将优势地称为简单优势，以区别于下面将讨论的累积优势。

2.2 累积优势

设 $z_i =\sum\nolimits_{ j = 1}^i x_j, \forall i$ 表示对象的累积轮廓。如果 $z^A_i\geq z^B_i, \forall i\textup{ and } \exists i \textup{ such that } z^A_i> z^B_i$ ，则称对象A累积优于对象B. 。如果对象A累积优于对象B，则可以确定A具有更高的标准值。要检查累积优势，需要知道特征权重递减的顺序，我们将其称为特征顺序。

简单优势蕴含累积优势。简单优势和累积优势都是可传递的：给定三个对象A，B和C，如果A优于B而B优于C，那么A优于C。

2.3 非补偿性

请考虑以下词典决策规则：按权重递减的顺序排列特征；识别区分对象之间的第一个特征；选择此函数值较高的对象。如果此决策规则正确地做出决策，我们会说决策问题表现为非补偿性。

如果特征是二元的，取值为0或1，并且权重满足约束集 ${w_i} > \sum\nolimits_{j = i + 1}^k {{w_j}} ,i=1,2, \ldots ,k - 1$ ，则以1的概率保持非补偿性。这种权重被称为非补偿性的。一个例子是序列1, 0.5, 0.25, 0.125。如果特征是数值的，则根据线性函数的权重和要比较的对象的特征值，非补偿性可能保持或不保持。

简单和累积优势都意味着非补偿性。

2.4 一个说明性的例子

作为一个说明性的例子，考虑一堆美国硬币，其中 $\left \langle x_{ \$ 1}, x_{50\cent},x_{25\cent},x_{10\cent},x_{5\cent},x_{1\cent} \right \rangle$ 表示钱堆中每种硬币类型的数量。钱堆的美元价值由线性函数 $x_{ \$ 1}+0.5 x_{50\cent}+0.25 x_{25\cent} + 0.1 x_{10\cent}+0.05 x_{5\cent}+0.01 x_{1\cent}$ 描述。

堆 $\left \langle 4,4,4,0,0,0 \right \rangle$ 简单优于堆 $\left \langle 3,4,2,0,0,0 \right \rangle$ 。即使硬币类型的美元价值未知，第一堆也可以被识别为具有较高价值的那一堆。

堆 $\left \langle 6,4,2,0,0,0 \right \rangle$ 累积优于（但不是简单优于）堆 $\left \langle 3,5,1,0,0,0 \right \rangle$ 。如果每种硬币类型的美元价值未知但硬币可以从最大价值到最低价值排序，则第一堆可以被识别为具有更高价值的那一种。

桩 $\left \langle 4,4,4,0,0,0 \right \rangle$ 既不简单优于也不累积优于堆 $\left \langle 2,8,2,0,0,0 \right \rangle$ 。词典决策规则选择第一堆，因为它包含更多最高价值的硬币类型。在这种特殊情况下这是正确的，但一般不保证是正确的 - 除非每堆最多具有每种硬币类型中的一种（因为权重是非补偿的）。

3.目标

序贯决策问题可以被视为一系列比较问题，尽管这些问题具有复杂的依赖性。在每个决策阶段，代理都会面临以下比较问题：在可用的操作中，选择具有最高值的操作。因此，如果学习算法适合于利用它们，那么使判断问题变得容易的相同类型的规则性也可能使序贯决策问题变得容易。我们的目标是探索这种可能性。

4.方法

我们研究俄罗斯方块，这是有史以来最知名和最受欢迎的视频游戏之一。游戏在二维网格上进行，最初是空的。不同形状的碎片从网格顶部落下，一次一个，彼此堆积在一起。当每个碎片落下时，玩家通过旋转棋子并将其水平向左或向右移动任意次数来控制棋子的放置位置和方式。当一行完全填满时，该行将被删除，从而在网格上创建额外的空间。当下一个棋子的网格顶部没有空格时，游戏结束。标准网格高20个单元，宽10个单元。这些碎片称为tetrimino，每个碎片占据四个单元并具有七种不同的形状。图1显示了游戏中的标准板和七种tetrimino。

图1.俄罗斯方块游戏中的示例板，显示从网格顶部掉落的tetrimino; 七个可能的tetriminos; 表格显示了BCTS使用的特征，它们在线性评价函数中的权重，以及它们在面板上的值，如果允许下降的tetrimino在没有干预的情况下掉落。这些函数在文中描述。

众所周知，有些tetrimino序列终止了游戏，无论它们的位置如何（Burgiel，1997）。即使事先已知整个tetrimino序列，找到tetriminos的最佳位置也是NP完全的（Demaine等，2003）。俄罗斯方块大约有 $1.6\times 10^{60}$ 个状态。

人工智能玩家可以学会玩得很好，平均删除数十万行。最着名的是BCTS（俄罗斯方块系统建造控制器），由Thiery＆Scherrer（2009）开发，他们使用BCTS的变体赢得了2008强化学习竞赛。控制器是使用交叉熵算法开发的，遵循Szita和Lorincz（2006）的早期工作。最近，强化学习方法成功地学习得更快，但没有学得更好的策略（Gabillon等，2013; Scherrer等，2015）。

BCTS使用具有八个特征的线性评价函数。对于从顶部掉落的每个tetrimino，控制器使用此线性评价函数评估面板上所有可能的合法放置，并选择具有最高值的放置。如果允许下降的tetrimino在没有干预的情况下掉落，则下面描述了这些特征并在图1中列出了它们的权重和面板上的值。

这些特征中使用的两个关键概念是孔和井。孔是一个空单元格，在同一列中有一个或多个完整单元格比自身高。井是列中的一列空单元，使得左侧和右侧的直接单元格填满（其中网格的外部假定为满）。

带孔的行是至少有一个孔的行数。
通过检查从一端到另一端的每列来计算列转换，并计算从完整单元格到空单元格或反向转换的次数。假设网格的外部在底部是满的，但在顶部是空的。
孔是孔的数量。
着陆高度等于 $(y_1 + y_2)/ 2$ ，其中 $y_1$ 和 $y_2$ 分别是当前tetrimino在清除任何行之前所占的最低和最高单元高度。
累积井是井中单元的累积深度，所有井的总和。例如，对于深度为3的井，其单元的累积深度为 1 + 2 + 3 = 6。
通过检查从一端到另一端的每一行来确定行转换，计算从完整单元到空单元的转换或反转的次数。假设网格外部已满（左侧和右侧）。
缺损的碎片单元是由放置清除的行数乘以与行一起清除的当前单元的单元格数。此函数的最大值为16（一次清除四行时）。
对于板上的所有孔，孔深度是在同一列中直接位于孔上方的被填住的单元数量的总和。

我们的第一个目标是检查游戏中遇到的状态，以确定以下条件的持续时间：简单优势，累积优势和非补偿。下面我们将介绍我们如何实施游戏以及我们如何收集数据。

4.1 我们的俄罗斯方块的实施

我们开发了两种俄罗斯方块，一种用于从人类收集数据，另一种用于使用人工玩家进行模拟实验。两种实施方案的标准面板尺寸均为 $10 \times 20$ 。下一个碎片是随机均匀选择的。每删除一行都会获得+1的奖励。在游戏中收到的总奖励称为分数。

人类受试者使用类似于标准视频游戏的游戏实现。 Tetriminos每次以舒适的速度从顶部掉落。当下一件不合适时，游戏终止。

另一方面，人工玩家的实施仅需要高度决定放置该块的位置和方向。此外，游戏略有简化，这在文献中是典型的（Szita＆Lorincz，2006; Thiery＆Scherrer，2009; Scherrer等，2015）。最上面四行仅用于显示下一件。合法的移动是那些可以通过在该显示区域中根据需要旋转和平移（向左或向右）然后放下它而进行的移动。当玩家无法将下一个棋子放入网格的下面16行时，游戏终止。

4.2数据采集

比赛期间遇到的状态取决于代理所遵循的策略。我们生成了三种不同的数据集，这些数据集在代理如何玩游戏时有所不同。每个数据集中的样本包括当前的面板配置和下一个要放置的块的标识。数据集如下所述。

BCTS是根据BCTS策略玩了20场比赛获得的。比赛得分介于49,013和3,381,366之间（中位数= 709,636）。从每场比赛中，我们选择了10,000个样本。

Random通过随机均匀地选择动作来获得，根据需要玩多个游戏以生成200,000个样本。随机策略很少清除线条，因此游戏非常短暂，持续12-36次移动（中位数为22），得分范围从0到5（中位数为0）。

People是邀请到愿意参与的13位熟人来玩游戏获得的。在记录他们的动作之前，每个参与者都有机会在他们自己选择的时间内练习游戏。参与者的游戏时间长度从172到4,230不等，中值为554。我们共收集了14,006个样本。

5.结果

在我们展示结果之前，我们定义一些术语。回想一下，样本包含当前的板配置和下一块的标识。一项行动是下一部分在当前面板的任何合法安置。概念集是可用操作的子集。我们定义了四种不同类型的考虑集：合法，不同，帕累托简单和帕累托累积，下面将详细解释。理想的位置是BCTS的线性评估函数排名最佳。由于多个放置位置可以具有相同的函数值，因此可能存在多个理想放置位置。

5.1 优势

图2显示了简单和累积优势的普遍性。该图显示了十二个图，显示了三个策略下四个考虑集的大小的经验概率分布函数。通过从上到下跟随每一列，可以观察到考虑集的大小的减少，因为在给定策略下，简单优势和累积优势被应用为过滤器。

Legal包含该作品的所有合法展示位置。它的概率分布在9,17和34处有三个峰值。这些是当有足够的空间时，板上可能放置的各种部分的数量。例如，方形tetrimino可以在空板上以九种不同的方式放置。当面板几乎满时，可能性的数量就会减少。随机策略比其他两项策略更频繁地经历一个满的面板，这就是为什么该策略的概率分布略有不同。

有时，两个不同的合法放置产生相同的特征值，这意味着BCTS控制器和使用相同特征的任何其他基于特征的控制器不会区分这些放置，为它们分配相等的值。

Distinct区分不同的法律集，除去其中一个特征值相同的合法放置位置。因此，此集合中的每个放置位置都有一组不同的特征值。

Pareto-simple通过进一步消除位置来区分不同的位置，这些位置仅由一个或多个其他位置支配。

Pareto-cumulative通过进一步消除由一个或多个其他位置累积的位置来区分Pareto-simple集（回想一下简单优势意味着累积优势）。优势的数学属性确保帕累托简单集和帕累托累积集包含至少一个理想位置。

图2.俄罗斯方块中简单和累积优势的普遍性。每个图显示了在遵循特定策略时考虑集的大小的经验概率密度函数（PDF）。所有图都以相同的比例绘制。轴标签仅显示在外图上。通过从上到下跟踪每列，可以观察到放置数量的减少，因为简单和累积优势被用作过滤器。

图2表明简单优势和累积优势都大大减小了考虑集的大小。所有三个策略都是如此。

在随机策略下，简单优势将候选选择的中位数从16减少到3，而累积优势进一步将其减少到2。换句话说，玩家平均有16个不同的位置需要考虑。通过简单地知道权重的符号（或正确猜测它们），玩家可以将此数字减少到3.如果特征顺序也已知，则此数字可以减少到2。

根据BCTS和人们遵循的策略，考虑集合的中值规模的减少幅度更大：从17到3，具有简单优势，到1具有累积优势。这很了不起。尺寸为1的考虑因素意味着没有做出决定：只剩下一个位置，并且可以肯定地知道这是一个理想的位置。

5.2 非补偿性

对于三个数据集中的每一个，我们应用如下的词典决策规则。我们从一系列独特的展示位置开始。我们按顺序使用每个特征，一次一个，以进一步减少放置的数量，直到只剩下一个元素为止。在每个特征中，我们只保留了此特征中具有最优（最高或最低，取决于特征权重的符号）值的放置，消除了所有其余部分。我们按照图1中列出的顺序使用了这些特征，这些特征对应于BCTS控制器的特征顺序。

非补偿率是样本决策是理想决策的样本比例。在BCTS，人类和随机控制器下，这个数字分别为68.1,69.0和52.0％。

图3.通过词典决策规则消除备选放置位置。实线表示在顺序应用前四个特征中的每一个之后剩余的备选方案的数量的经验累积分布函数（CDF）。请注意，在两个数据集（BCTS和People）上，属于1-3的行几乎相同。加号表示在处理特征1后仍然在考虑理想备选的情况的比例：如果比例为1，则加号在实线灰色线上。

图3显示了每个数据集的过程。纵轴表示经验累积分布函数（CDF）。特征1（带孔的行）大大减少了所考虑的替代方案，同时通常保持理想的替代方案。具体来说，它将动作的中位数从17减少到4,9,4，同时在BCTS，随机和人数据集中，分别98％，99％和93％的案例中保留了理想动作。

5.3 整体能力

我们在三个附加策略下检查了轨迹：在帕累托简单集中随机选择，在帕累托累积集中随机选择，以及遵循样本决策规则。图4显示了这些策略获得的分数的分布。为了跟直观理解这些数字，想象达到80分相当于清理合法放置区域（16行）5次。

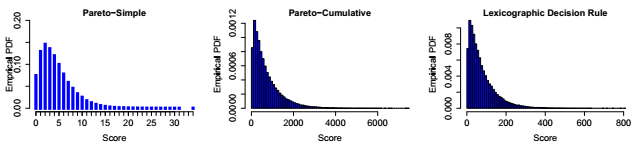
图4.通过利用简单优势，累积优势和非补偿的策略获得的分数。相比之下，随机选择动作的控制器几乎总是以0分结束游戏，而BCTS分数在49,013和3,381,366之间（中位数= 709,636）。

我们还计算了沿着轨迹随机选择的样本做出理想选择的概率。对于在Pareto-simple中选择的策略，该数字为0.38，对于Pareto-cumulative而言为0.75。

6.讨论

我们的分析表明，简单优势，累积优势和非补偿性在俄罗斯方块中都很普遍。此外，还有一个特征（带孔的行）可以消除大量的操作，而很少消除最佳操作。此特征并不复杂，但简单直观。

我们的研究结果引发了两个问题。首先，俄罗斯方块在具有这些属性的连续决策问题中是独一无二的还是罕见的？第二，算法如何利用这些属性进行更有效的学习？我们依次讨论每个问题。

6.1 俄罗斯方块特殊吗？

我们的结果反映了早期关于自然环境中一次性决策问题的发现。在比较对象时，发现优势和非补偿是普遍存在的（Säims¸ek，2013）。此外，在分类和比较问题中报告了一个非常强大的特征，即能够自行处理大部分工作量的特征（Holte，1993;Säimsek＆Buckmann，2015）。鉴于在更简单的问题中有类似的发现，并且鉴于俄罗斯方块是我们分析的第一个连续决策问题，俄罗斯方块似乎不太可能是特殊的。我们在步步高游戏中进行的有限分析也支持了这种观点。

双陆棋是众所周知的最古老的棋盘游戏之一，在许多地区深受喜爱。它有超过1020个可能的面板位置。 1979年，由Berliner（1980）开发的手工制作的人工玩家击败了人类世界冠军。后来，Tesauro（2002）开发了一个更好的玩家，通过使用神经网络的自我游戏来学习，其游戏水平超过了最好的人类玩家。

我们分析了1838盘世界顶级锦标赛中的双陆棋游戏，包括1973年至2011年的蒙特卡洛世界锦标赛。我们从Hubener维护的在线存储库中获取数据，以检查简单优势的普遍性。我们检查了两个对手仍然接触的位置 - 否则，游戏大大简化并且主要取决于滚动的运气。这给了我们55,442个样本进行检查。我们使用以下特征，在括号中指示的方向：点数（-），印迹暴露（-），在面板上的点数（+），初期形成（+），对手的点数（+），对手的印迹暴露（+）。

应该指出的是，双陆棋是一种复杂的战略游戏。玩家遵循不同的高级策略，例如跑，阻挡或后退，在这些策略下，所需的棋子动作非常不同。例如，虽然通常需要较低的点数，但是当正在后退时，较高的点数是有利的。我们提出的只是粗略的分析，没有考虑上下文。

图5显示了结果。双陆棋可以具有高分支因子，特别是如果骰子显示双倍。骰子的合法游戏数量范围从0到515（中位数= 13;第95百分位数= 64）。相反，帕累托简单集的大小范围为0到259（中位数= 5;第95百分位数= 22）。在77.8％的样本位置中，锦标赛选手所选择的动作是在帕累托简单的集合中。

6.2 学习算法如何利用这些属性？

一种可能性是将代理的动作选择减少为Pareto-simple和Pareto-cumulative集。我们举两个例子。首先，我们使用Bertsekas＆Tsitsiklis（1996）描述的相同特征和参数将近似 - 策略迭代应用于俄罗斯方块。每次迭代使用100,000个样本。其次，我们应用了AmpiQ，它属于近似修改的策略调整（AMPI）算法的家族（Scherrer等，2015）。我们使用的卷展设置大小为20,000，卷展长度为15.我们使用了图1中列出的特征以及Lagoudakis等人使用的特征。（2002年）。

图6. -Policy迭代（-PI）和AmpiQ应用于俄罗斯方块，无论是否减少了对Pareto集的可用操作。该图显示了每次迭代的中值分数的分布（100次重复）。实线连接中值，而阴影区域显示第25和第75百分位数。 AmpiQ的分数以对数标度显示。没有Pareto集的AmpiQ的第一次迭代返回的分数中位数为0（图中未显示）。

图6显示了使用图1中列出的特征，有或没有首先将动作集减少到Pareto-simple和Pareto-cumulative的学习曲线。该图显示了每次迭代的中值分数的分布（100次重复）。实线连接中值，而阴影区域显示每百万分之25和75。学习曲线显示学习率和所学策略的质量明显提高。

另一个有前途的研究方向是研究非常简单的策略。优势和非补偿允许简单的规则，例如词典和计数的启发式算法（Gigerenzer等，1999），在一次性问题中做出正确的决定。受这些启发式启发的非常简单的策略可能能够在与环境的短期交互中学习合理的策略。

7.结束语

这项工作探索了学习解决序贯决策问题的新方向，利用各种研究领域的见解，如认知心理学和运作研究。我们检查了三个数学特性 - 它们是否有助于做出一次性决策 - 也适用于序贯决策。我们发现这些属性很普遍，可以在俄罗斯方块和双陆棋游戏的学习算法中嵌入。

如前所述，未来的两个重要方向是研究其他顺序决策问题，并探讨学习算法如何进一步利用这些属性。其他研究方向包括：（1）在识别帕累托集时考虑上下文，（2）使用原则概率近似来简单和累积优势（Säimsek，2013），（3）探索简单优势用于非线性值函数 - 我们只讨论了优势对于线性函数，但简单的优势适用于更广泛的函数集。

传统上，很难将领域知识注入到强化学习算法中。这里描述的工作为某些类型的领域知识提供了一种简单的方法。构建帕累托简单集和帕累托累积集所需的知识类型，或者它们的近似，可以在许多领域中容易地获得。例如，在俄罗斯方块中，特征方向都很直观，这使得Pareto简单集很容易构建。

我们的研究结果为研究自然决策问题提供了有力的理由。虽然合成域在开发学习算法中起着重要作用，但研究自然问题的结构规律可以为有效学习提供额外的见解。