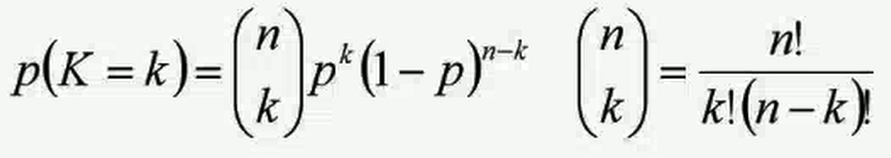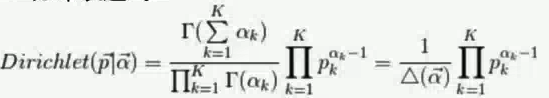1. 回顾主题模型

• 主题模型是一种生成模型，一篇文章中每个词都是通过“以一定概率选择某个主题，并从这个主题中以一定概率选择某个词语”这样一个过程得到: $p(word|doc)=\sum_{topic}p(topic|doc)*p(word|topic)$
• 主题模型客服了传统信息检索中文档相似度的计算方法，并能在海量的数据中找出文字间的语义主题。主题模型在自然语言和文本搜索上起到了重要的作用。

1.1 SVD奇异值矩阵分解

• 重点是将其转换为一个矩阵：
  $p(词语|文档)=\sum_{主题}p(词语|主题)*p(主题|文档)$
  
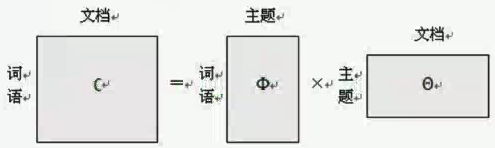
  主题模型就是一个SVD矩阵分解，得到一个奇异值矩阵。
  
  对于奇异值，它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别快，在很多情况下，前10%甚至前1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个奇异值和对应左右奇异值向量来近似描述矩阵。 $A_{m*n}=U_{m*m} \sum_{m*n}V_{n*n}^T \approx U_{m*k} \sum_{k*k}V_{n*k}^T$
• 由于可以使用小矩阵来近似的描述样本信息的这个重要特征，SVD可以常用于PCA降维、推荐系统以及主题模型等场景中。

1.2 LSA (Latent Semantic Analysis, LSA)

潜在语义分析（Latent Semantic Analysis, LSA）是一种常用的简单主题模型。LSA是基于奇异值分解（SVD）方法得到的一种文本主题方式。
$A_{m*n} = U_{m*m} \sum_{m*n}V_{n*n}^T$
$A_{m*n} \approx U_{m*k} \sum_{k*k}V_{n*k}^T$
总结：我们输入的有m个文本，每个文本有n个词。而 $A_{ij}$对应第 $i$个文本的第 $j$个词的特征值。 $k$是我们假设的主题数，一般要比文本数少。SVD分解后， $U_{il}$对应的第 $i$个文本和第 $l$个主题的相关度。 $V_{jm}$对应第 $j$个词和第 $m$个词义的相关度。 $\sum_{lm}$对应第 $l$个主题和第 $m$个词义的相关度。

通过SVD矩阵我们可以得到文本、词与主题、语义之间的相关性，但是这个时候计算出来的内容存在负数，我们比较难解释。最终我们可以对LSI得到文本主题矩阵使用余弦相似度计算文本的相似度计算。最终我们得到第一个和第三个文档比较相似，和第二个文档不太相似。（备注：这个时候直接在文本主题矩阵的基础上直接应用聚类算法即可）。
除非数据规模比较小，而且希望快速的粗粒度找出一些主题分布关系，否则我们一般不会是使用LSA主题模型。
优点

• 原理简单，一次SVD分解即可得到主题模型，同时可以解决词义的问题。
  缺点
• SVD分解的计算非常耗时，对于高纬度矩阵做SVD分解非常困难；
• 主题模型数量的选取对于结果影响非常大，很难选择合适的k值；
• LSA模型不是概率模型，缺乏统计基础，结果难以直观的解释。

1.3 pLSA

pLSA的另一个名称是Probabilistic Latent Semantic Indexing(pLSI)，假定在一篇文档d中，主题用c来表示，词用w来表示，则有下列公式：
$p(w,d) = \sum_c p(c)p(d|c)p(w|c)=p(d)\sum_c p(c|d)p(w|c)$
文档积决定了我的主题：
$p(w|d) = \frac{p(w,d)}{p(d)}=\sum_c p(c|d)p(w|c)$
$p(词语|文档)=\sum_{主题}p(词语|主题)xp(主题|文档)$

文档决定主题，主题决定单词，这就是这样的一个结构

2. LDA以及狄拉克雷分布

2.1 概率知识回顾

2.1.1 先验概率、后验概率及似然函数

• 先验概率：在事情尚未发生之前，对事情发生的概率的估算。利用过去历史资料计算出来得到的先验概率叫做客观先验概率；凭主观经验来判断而得到的先验概率叫做主观先验概率。

• 后验概率：通过调查或其他方式获取新的附加信息，利用贝叶斯公式对先验概率进行修正后，而得到的概率。可以说是通过一个调查问卷的形式进行。

• 似然函数：给定模型参数 $\theta$的条件下，样本数据服从这一概率模型的相似程度。
  $p(\theta_i|X)=\frac{p(X|\theta_i)p(\theta_i)}{\sum_j p(X|\theta_j)p(\theta_j)}$
  在这个公式中， $p(X|\theta_i)p(\theta_i)$可以看成是一个先验概率， $p(X|\theta_i)$是一个似然函数，而最后得到的 $p(\theta_i|X)$可以认为是一个后验概率。其中 $\theta_1,\theta_2,...$表示模型的未知参数，X表示样本。我们得到的是一个后验概率。

• 先验分布：反映在进行统计实验之前根据其他有关知识得到的分布，也就是说在观测获取样本之前，人们已经对 $\theta$有一些认识，此时这个 $\theta$的分布函数为 $H(\theta)$， $\theta$的密度函数为 $h(\theta)$，分别称为先验分布函数和先验密度函数，统先验分布。

• 后验分布：根据样本X的分布以及 $\theta$的先验分布 $\pi (\theta)$，使用概率论中求解条件概率的方式可以计算出来已知X的条件下， $\theta$的条件分布 $\pi (\theta)$，因为获取该分布是在获取样本x之后计算出来的，所以称为后验分布。

2.1.2 共轭分布、二项分布及多项分布

• 共轭分布：如果先验分布和后验分布具有相同的形式，那么先验分布和似然函数被称为共轭分布。
• 二项分布：二项分布称为0-1分布，是一个离散值的随机分布，其随机变量只有两类取值，非负即正{+，-}。而二项分布即重复n次伯努利实验，记为 $X\approx b(n,p)$。言而言之，只做一次实验，是伯努利分布，重复做了n次，就是二项分布。二项分布的概率密度函数为：
  
  
  
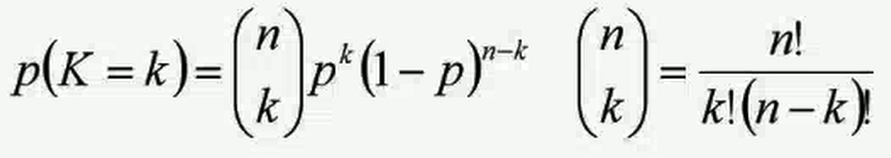
• 多项分布：是二项分布的推广，那么它的取值不再是0/1，可以有(1,2,3,4,…,k)。比如投掷6个面的骰子实验，N次实验结果服从K=6的多项分布，其中K个离散值的概率为： $\sum_{i=1}^k = 1$（必为1），多项分布的概率密度函数为：
  $X = (x_1,x_2,...,x_n)$
  $p(x_1=m_1,x_2=m2,...,x_k=m_k,n,p_1,p_2,...,p_k)=\frac{n!}{m_1!m_2!...m_k!} p_1^{m_1}p_2^{m_k}...p_1^{m_k}$

2.1.2 Beta分布及Dirichlet分布

• Beta分布：就是二项分布的共轭分布，指一组定义在(0,1)区间的连续概率分布，具有两个参数 $\alpha,\beta > 0$
  
  除去系数不看，可以发现先验概率和后验概率都属于Beta分布，所以认为Beta分布和二项分布属于共轭分布。

• Dirichlet分布：Dirichlet分布是由Beta分布推广而来的，是多项式分布的共轭分布。
  $f(x_1,x_2,...,x_k,\alpha_1,\alpha_2,...,\alpha_k)=\frac{1}{B(\alpha) \sum_i=1^k x_i^{(\alpha_{i-1})}}$ $\alpha = (\alpha_1, \alpha_2, ..., \alpha_k)$

2.2 Latent Dirichlet Allocation，LDA

隐含狄拉克雷分布Latent Dirichlet Allocation，LDA是一种基于贝叶斯算法模型，利用先验分布对数据进行似然估计并最终得到后验分布的一种方式。LDA是一种比较常用的主题模型。

• LDA假设文档主题是多项分布，多项分布的参数（先验分布）是服从Dirichlet分布，其中，LDA是一种常见的三层贝叶斯模型。
  
  $\alpha$是一个先验知识， $\theta$是文档的多项式分布， $z$是文章属于哪个主题。
• 共有M篇文档，每个文档有 $N_m$个单词，一共涉及到K个主题；
• 每篇文档都有各自主题，主题分布是多项式分布，该多项式分布是服从Dirichlet分布，该Dirichlet分布的参数为 $\alpha$；
• 每个主题都有各自的词分布，词分布为多项式分布，该多项式分布的参数服从Dirichlet分布，该Dirichlet分布的参数为 $\eta$；
• 对于某篇文档d中的第n个词，首先从该文档的主题分布中采用一个主题，然后再这个主题对应的词的分布中采用一个词，不断重复该操作，直到m篇文档全部完成上述过程。

2.2.1 LDA详细讲解

• 词汇表中共有V个词（不可重复）；
• 语料库中共有m篇文档 $d_1,d_2,...,d_m$，对于文档 $d_i$，是由 $N_i$个word组成（word可重复），语料库中共有K个主题 $T_1,T_2,...,T_k$
• $\alpha$和 $\eta$是先验分布（Dirichlet分布）的参数
• $\theta$是每篇文档的主题分布，是一个K维的向量；
• 对于第i篇文档 $d_i$，在主题分布 $\theta_i$下，可以确定一个具体的主题 $z_{ij}=k$
• $\beta$是每个主题的词分布，是一个 $V$维的向量；
• 由 $z_{ij}$选择 $\beta_{zij}$（单词概率），表示由词分布 $\beta_{zij}$确定term，即可得到最终的观测值 $w_{ij}$。

2.2.2 LDA构建流程

LDA在进行文本的主题模型构建的时候，对于D的文档，K个主题的模型构建流程如下：

• 1.对于每一个Topic k，计算出 $\beta$的值： $\beta_k \approx Dirichlet(\eta), k=1...K$
• 2.对于每一个Document d，计算出 $\theta$的值： $\theta_d \approx Dirichlet(\alpha), d=1...D$
• 3.对于Document d中的word:
• 3.1 计算所属的topic z值， $z_{di} \approx Multinomial(\theta_d)$
• 3.2 计算出观测到的单词w， $w_{ij} \approx Multinomial(\beta_{z_{di}})$
• 4.对于 $\alpha、\beta、z$的参数估计，基于贝叶斯算法可以得到如下公式：
  $p(z,\theta,\beta|w,\alpha,\eta) = \frac{p(z,\theta,\beta,w,\alpha,\eta)}{p(w,\alpha,\eta)}=\frac{p(z,\theta,\beta,w|\alpha,\eta)p(\alpha,\eta)}{p(w|\alpha,\eta)p(\alpha,\eta)}=\frac{p(z,\theta,\beta,w|\alpha,\eta)}{p(w|\alpha,\eta)}$
  

2.2.3 LDA参数学习-Gibbs采样

• 对于一个n维的概率分布 $\pi (x_1, x_2,...,x_n)$，可以通过n个坐标上轮换采样，来得到新的样本，对于轮换到任意一个坐标 $x_j$上的转移，马尔科夫链的状态转移概率为 $p(x_i|x_1,x_2,...,x_{i-1},x_{i+1},...,x_n)$，即固定n-1个坐标轴，在某一个坐标上移动

• Gibbs采样算法在高维空间采样的时候具有比较高的优势，Gibbs采样的过程比较类似这个坐标轴下降法。其过程如下：

• 1.输入稳定的分布 $\pi(x_1,x_2,...,x_n)$或者对应特征的条件概率分布，设定状态转移次数阈值 $n_1$，需要的样本数 $n_2$

• 2.随机初始化状态值 $(x_1^1,x_2 ^1,...,x_n^1)$

• 3.进行迭代数据采样（迭代 $n_1+n_2 - 1$次），前面 $n_1$轮是不要的

  • 从条件概率分布中采样得到对应的样本： $x_j^{t+1}->p(x_j|x_1^{t+1},x_2^{t+1},...,x_{j+1}^{t+1},...,x_n^{t+1})$

• 4.最终得到的样本集为：
  ${(x_1^{n1},x_2^{n1},...,x_n^{n1}),...,(x_1^{n_1+n_2-1},x_2^{n_1+n_2-1},...,x_n^{n_1+n_2-1})}$

那么LDA如何用于现实的一个学习采样呢？

• 给定一个文档集合， $w$是可以观察到的值， $\alpha$和 $\eta$是根据经验给定的先验参数，其它的各个 $z、\theta、\beta$都是未知的隐含变量，都是需要根据观测到的数据进行学习的。

• 具体来讲，所有文档联合起来形成的词向量 $w$是已知数据，但是不知道语料库的主题 $z$的分布。假设可以先求出 $w、z$的联合分布 $p(w,z)$，进而就可以求出某个词 $w_i$对应主题特征 $z_i$的条件概率分布 $p(z_i=k|w,z_{-i})$，其 $z_{-i}$表示去掉下表为 $i$后的主题分布，有了条件概率，那么就可以使用 $Gibbs$采样，最终可以得到第 $i$个词的主题。

  • 这段意思是先求出来某个单词 $w$与某个主题 $z$的联合分布，就可以得到某个单词 $w_i$对应主题的特征条件概率分布 $p(z|w)=\frac{p(w,z)}{p(w)}$，这里是基于贝叶斯公式。 $p(z_i=k|w,z_{-i})$中利用到了 $Gibbs$采样，也就是我们已知道主题的概率分布 $\pi (z_1, z_2,...,z_n)$下，我们可以得到最终的主题采样数据集为 ${(z_1^{n1},z_2^{n1},...,z_n^{n1}),...,(z_1^{n_1+n_2-1},z_2^{n_1+n_2-1},...,z_n^{n_1+n_2-1})}$

• 如果通过采样得到所有词的主题，那么可以通过统计所有词的主题数，从而得到各个主题的词分布。接着统计各个文档对应的主题数，从而可以得到各个文档的主题分布。

  • 这里是表示当我们已经知道单词的数目，那么利用 $w$与 $p(z_i=k|w,z_{-i})$相乘后，就可以得到文档的主题分布，这里重点在于求单词 $w$与主题 $z$的联合概率分布 $p(w,z)$以及某个词 $w_i$对应主题特征 $z_i$的条件概率分布 $p(z_i=k|w,z_{-i})$。

根据上述所求问题，我们就给出一个简化的Dirichlet分布：

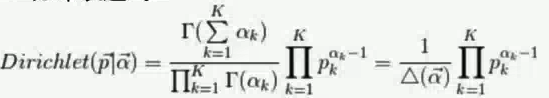
• 计算文档的主题条件分布
  当我们给定 $a->b->c$，求 $P(c|a)$，这里等于 $P(b=1|a)$乘以 $P(c|b=1)$加上一个微分的形式，如下图所示：
  
  在第 $d$个文档中，第 $k$个主题的词的个数表示为： $n_d^(k)$，对应的多项分布的计数可以表示为：
  ${n}_d^{\rightarrow}=(n_d^1,n_d^2,...,n_d^K)$
  其中 $n$表示主题的数目， $k$是属于第几篇文章。
  
  整个过程如下：
• 1.选择合适的主题数 $K$，选择合适的超参数 $\alpha、\eta$
• 2.对于语料库中每一篇文档的每一个词，随机赋予一个主题编号 $z$。
• 3.重新扫描语料库，对于每一个词，利用 $Gibbs$采样公式更新它的 $topic$编号 ，并更新语料库中该词的编号。
• 4.重复第三步中基于坐标轴轮询的 $Gibbs$采样，直到 $Gibbs$采样收敛。
• 5.统计语料库中各个文档各个词的主题，得到文档主题分布；然后统计语料库中各个主题分布，得到主题与词的分布。

2.2.4 LDA与pLSA之间的区别

LDA是比PLSA更“高级”的一种topic model。