熵

在信息论中，熵（entropy）是表示随机变量不确定性的度量，如果一个事件是必然发生的，那么他的不确定度为0，不包含信息。假设 $X$是一个取有限个值的离散随机变量，其概率分布为：
$P(X=x_i)=p_i$
则随机变量 $X$的熵定义为：
$H(X)=-\sum_{i=1}^np_ilog(p_i)$
通常上式中 $log$的底数为2或 $e$（自然对数），这时熵的单位分别称作比特（bit）或纳特（nat）。并且通过上述定义可知，熵的取值只依赖于 $X$的分布，而与 $X$的具体值无关。
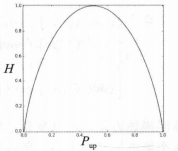
以 $P=0.5$的二项分布为例，熵 $H$随概率 $p$变化的曲线如下所示：

条件熵

设有随机变量 $(X, Y)$，其联合概率分布为：
$P(X=x_i,Y=y_j)=p_{ij},\ i=1,2,...,n;\ j=1,2,...,m$
条件熵（conditional entropy）表示在已知随机变量 $X$的条件下随机变量 $Y$的不确定性，定义为 $X$给定条件下 $Y$的条件概率分布的熵对 $X$的数学期望：
$H(Y|X)=\sum_{i = 1}^{n}p_iH(Y|X=x_i),\quad p_i=P(X=x_i),i=1,2,...,n.$
在计算条件熵时，需要先分别计算 $X$取不同值时变量 $Y$的熵，即 $H(Y|X=x_i)$，总共 $n$个（假设 $X$有 $n$种不同取值），然后求其对 $X$的期望。

互信息

互信息，在机器学习（决策树算法）中也称为信息增益。特征 $A$对训练数据集 $D$的信息增益 $g(D,A)$，定义为集合 $D$的经验熵 $H(D)$与特征 $A$给定的条件下 $D$的经验条件熵 $H(D|A)$之差，即：
$g(D|A)=H(D)-H(D|A)$

联合熵

联合熵度量的是一个联合分布的随机系统的不确定度，同样以联合概率分布 $(X, Y)$为例， $P(X=x_i,Y=y_j)=p_{ij},\ i=1,2,...,n;\ j=1,2,...,m$，则联合熵 $H(X,Y)$的定义为：
$H(X,Y)=-\sum_{i=1}^{n}\sum_{j=1}^{m}p_{ij}log(p_{ij})$
联合熵具有以下性质（对于变量数目大于2的情况同样成立）：

1. 联合熵大于其中任一变量独立的熵： $H(X,Y)>max\{H(X),H(Y)\}$
2. 联合熵小于所有变量独立熵之和： $H(X,Y)<H(X)+H(Y)$
3. $H(X,Y)=H(Y|X)+H(X)=H(X|Y)+H(Y)$
4. $g(Y|X)=H(X)+H(Y)-H(X,Y)$