参考链接:https://blog.csdn.net/luotuo44/article/details/41645597
参考链接:https://blog.csdn.net/shelldon/article/details/54729687
伽罗华域定义

我对伽罗华域的理解就是,给定一个域,比如4位,在4位之内的数字,不管加、减、乘、除,结果都在域里面,不会溢出,并且。运算时可逆的,能够还原
比如4位最大数字为15,那么13+14 = a不能超过15,并且运算可逆:a - 13 = 14, a - 14 = 13
同样13 x 14 = a,a不能超过15,a / 13 = 14
伽罗华域的计算

有限域
在密码学中,有限域GF(.p)是一个很重要的域,其中p为素数。简单来说,GF(.p)就是 mod p,因为一个数模p后,结果在[0, p-1]之间。对于元素a和b,那么(a+b) mod p和(a*b)mod p,其结果都是域中的元素。GF§里面的加法和乘法都是平时用的加法和乘法。
为什么p必须是素数?
是因为当p为素数时,才能保证集合中的所有的元素都有加法和乘法逆元(0除外)。
举个例子:加入p = 10,那么我们需要计算1 / 2,也就是计算a,使得(a * 2) mod 10 = 1,但是显然没有这样的a成立。
本原多项式
既然要求p是素数,那么有没有对不同的域的大小一个特定的素数呢,这个是有一些经常使用的素数的,转换成多项式叫做本原多项式
例如在24域里面,多项式为:x4+x+1,也就是二进制10011,因为需要异或这个多项式,所以多项式的最高位肯定是2w,然后后面加一个素数,在w为4的时候,这个素数就是3。

通过本原多项式生成元素
按照之前的算法


GF(24)含有16个元素,本原多项式为P(x)=x^4+x+1,除了 0、1外,另外14个符号均由本原多项式生成。
可以看到最后一个元素的计算过程,正好对P(x)取模之后,结果为1

生成元素代码(正表构造)
for i in range(1, gf_element_total_number - 1):
temp = gfilog[i - 1] << 1 # g(i) = g(i-1) * 2
if temp & gf_element_total_number: # 判断溢出
temp ^= primitive_polynomial # 异或本原多项式
gfilog.append(temp)
结果
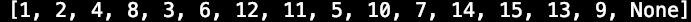
这个将生成元变为多项式,然后映射到十进制的形式,也就是将生成元的系数映射成十进制的形式。
反表构造
当我们需要逆元的时候,就需要将十进制变为多项式,例如我们知道gfilog[0] = 1,那么我们需要知道gfilog[x] = 1的x
这个时候就需要构建反表gflog
gflog的构造方式为:gflog[gfilog[i]] = i
也就是根据二进制,转换为生成元。
for i in range(0, gf_element_total_number - 1):
gflog[gfilog[i]] = i
结果:

那么就构造出来了两个表了。

伽罗华域四则运算
1.加法运算
异或然后对2w取模即可
2. 减法运算
与加法一样,异或然后对2w取模即可
def add(self, a, b):
return (a ^ b) % self.total
def sub(self, a, b):
return (a ^ b) % self.total
3. 乘法运算
- 将十进制变为多项式:查gflog表
- 两个多项式相加,如果溢出,对2w取模
- 将多项式变为生成元:查gfilog表
def mul(self, a, b):
return self.gfilog[(self.gflog[a] + self.gflog[b]) % self.total]
4. 除法运算
既然乘法是相加,那么除法就反过来相减。
- 将十进制变为多项式:查gflog表
- 两个多项式相减,如果溢出,对2w取模
- 将多项式变为生成元:查gfilog表
def div(self, a, b):
return self.gfilog[(self.gflog[a] - self.gflog[b]) % self.total]
完整程序
输入:伽罗华域位大小4、8、16、32、64
输入:两个数字
输出:四则远算的结果
primitive_polynomial_dict = {4: 0b10011, # x**4 + x + 1
8: (1 << 8) + 0b11101, # x**8 + x**4 + x**3 + x**2 + 1
16: (1 << 16) + (1 << 12) + 0b1011, # x**16 + x**12 + x**3 + x + 1
32: (1 << 32) + (1 << 22) + 0b111, # x**32 + x**22 + x**2 + x + 1
64: (1 << 64) + 0b11011 # x**64 + x**4 + x**3 + x + 1
}
class GF:
def __init__(self, w):
self.w = w
self.total = (1 << self.w) - 1
self.gflog = []
self.gfilog = [1] # g(0) = 1
self.make_gf_dict(self.w, self.gflog, self.gfilog)
def make_gf_dict(self, w, gflog, gfilog):
gf_element_total_number = 1 << w
primitive_polynomial = primitive_polynomial_dict[w]
for i in range(1, gf_element_total_number - 1):
temp = gfilog[i - 1] << 1 # g(i) = g(i-1) * 2
if temp & gf_element_total_number: # 判断溢出
temp ^= primitive_polynomial # 异或本原多项式
gfilog.append(temp)
assert (gfilog[gf_element_total_number - 2] << 1) ^ primitive_polynomial
gfilog.append(None)
for i in range(gf_element_total_number):
gflog.append(None)
for i in range(0, gf_element_total_number - 1):
gflog[gfilog[i]] = i
print(gflog)
print(gfilog)
def add(self, a, b):
return (a ^ b) % self.total
def sub(self, a, b):
return (a ^ b) % self.total
def mul(self, a, b):
return self.gfilog[(self.gflog[a] + self.gflog[b]) % self.total]
def div(self, a, b):
return self.gfilog[(self.gflog[a] - self.gflog[b]) % self.total]
测试
gf = GF(4)
import random
t = 0
while t <= 20:
a = random.randint(1, 15)
b = random.randint(1, 15)
c = gf.add(a, b)
d = gf.mul(a, b)
print('%d + %d = %d' % (a, b, c))
print('%d - %d = %d' % (c, a, gf.sub(c, a)))
print('%d * %d = %d' % (a, b, d))
print('%d / %d = %d' % (d, a, gf.div(d, a)))
print()
t += 1

从结果中可以看到2+10=8
8-10=2,说明加减法是可逆的
2 x 10 = 7
7 / 2 = 10,说明乘法除法是可逆的