我们知道逻辑回归的算法：

依据逻辑函数：也称为Sigmoid函数。而线性回归中的表达式：hθ(x)=θTx，显然无法限定输出到0,1之间（即不能进行逻辑回归分类）。所以逻辑回归的函数表达式 表示为：hθ(x)=g(θTx)。这里g称为Sigmoid函数，表达式为：g(z)=1/(1+e-z)，z和g(z)满足图形如下：

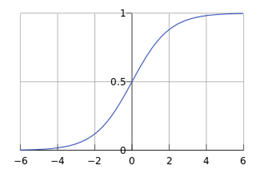
如何确认预测函数Sigmoid函数的θ值呢，当然是最小化代价函数，我们知道Sigmoid函数对应的代价函数为：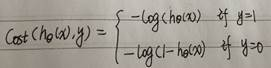

将上边的统一成一个代价函数

可以从上图的知道当y=1时z越小(Sigmoid函数对应值距离1越远)，代价值越大，y=0时反之

在已知代价函数的基础，将训练集代入，最小化代价函数，如何最小化代价函数呢？通过求导，然后在进行梯度下降确定θ值即可.

演化到支持向量机

我们将上图的代价函数进行修改，我们假设存在某个cost函数(真正理解了支持向量机后你就会知道这就是支持向量机的代价函数的样子)满足以下红色代价函数图像：

                  当y=1时满足cost1(z)图，                                                            当y=0时满足cost0(z)图

由上图可知当y=1时若z>=1则认为代价为0，y=0时反之

我们知道在逻辑回归中为了防止过拟合和一些异类数据的影响我们会增加正则项，来降低各属性对确定最终的θ值的影响

因此逻辑回归带有正则项的代价函数是：

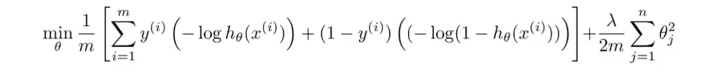
将此式中的对应位置使用上边我们说的cost1和cost0代替转化为：其中约掉了1/m，并乘以C(C=1/λ)得到下式

若要最小化此代价方程，则需要：

当y=1时，令θTx>=1,则对应cost1代价为0

当y=0时，令θTx<=-1,则对应cost0代价为0

同时在满足上边条件的一组θ又要同时兼顾令最小化，即令θTθ最小化，即令θ的矢量长度|θ|最小化，下边解释一下为什么说就是θ的矢量长度最小化

矢量长度：我们知道矢量v=(x1,y1,z1) 的长度等于x1²+y1²+z1² 的和开方，同理矢量θ的长度|θ|等于θTθ的结果开方，

则=1/2*θTθ=1/2|θ|²

又有高中数学知识我们知道 有向量V(x1,y1)和U(x2,y2) 则VTU=x1*x2+y1*y2 而其在数学上的几何意义等于V在U上的投影长度乘以U的长度也等于U在V上的投影长度乘以V的长度,因此θTx=x在θ上的投影p乘以θ的长度|θ|=p|θ|，值得说明的是p值有正负之分，

那么我们可以初步了解到支持向量机就是在做下边的事情

A：

最小化1/2|θ|²

B:

令θ满足

y=1时θTx>= 1  ==>  |p|*|θ|>=1

y=0时θTx<=-1  ==>  -|p|*|θ|<=-1

在满足A条件的同时还要令θ满足B的条件（理想中是这样，但因为训练集中不乏一些异常值，或者样本边界并不十分明确，这时候A和B就要互相做出让步,这就是代价函数中C常数的作用，这里不做细说，也就是在尽量满足B的同时最小化A，为了很好的理解支持向量机在干嘛，我们先不去考虑这些情况）

从B的条件来看我们就是就是在找一个向量θ是正样本在其上的投影是正值且尽量的长，负样本在其上的投影是负值且尽量长

上图中〇代表正样本x1,x2,x3  △代表负样本x4,x5,x6   而支持向量机就是在找一个向量θ使其满足我们上边的提到的投影要求，并且其样本间隔就是2倍的1/θ,如图中所说若θ是单位向量则其间隔刚好为2，这也就是为什么它也被叫做大间隔分类算法。图中我们的样本属性只有两个特征——横坐标值和纵坐标值，而大多数情况下特征都不止两个，但同样也能找到一个矢量θ使其满足条件，因此持向量机的这种二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面

回过头来我们再来细细理解一下这个支持向量机的代价方程，想象一下C的作用（C>0）

我们用极限的思想去想象一下如果C趋近于无穷大时候，只需要让

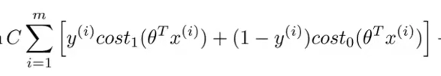这一项最小化就可以了，这样根据代价方程的图形我们知道只要存在一个超平面使得让y=1时θx的乘积>0 或者y=0时θx的乘积<0，即超平面尽量多的将正负样本分离，那么我们就可以通过放大θ使得让y=1时θx的乘积>=1 或者y=0时θx的乘积<=-1这样对应的代价值就是0，通过控制θ的放大倍数来确认一组最小的θ，如果令C趋近于零，我们知道只需要后边最小值就可以，显然毫无意义，如果C适度则我们就不能只是不计后果的通过放大θ来满足只要超平面尽量多的分开正负样本达到第一项的最小值，而是要兼顾加上后边的来整体达到最小，这样就会牺牲一些异类样本，使得算法更具有鲁棒性