转置卷积

转置卷积源于与卷积方向相反的愿望，即从卷积的output形状到input形状，同时保持与卷积相兼容的一种模式。转置卷积可以作为卷积编码器的解码器(decode)的转换，或者将当前特征映射到一个高维度的空间。

Convolution as matrix operation

要理解转置卷积，先从卷积开始。
我们先从2D卷积运算，kernel=3，input=4x4，stride=1，output=2x2，padding=valid。
我们将卷积运算转化为矩阵运算，将kernel转化为矩阵 $C_{4X16}$的，将input转化为矩阵 $X_{16X1}$，通过两个矩阵的相乘获取的 $Y_{4X1}$矩阵reshape为2X2的卷积结果。即 $Y_{4X1}=C_{4X16}X_{16X1}$
我们以C的第一行为例，第一行要完成与input[:3,:3]乘加，其他不需要乘的对应权重则在这一行置为0。也可以这样理解，这一行的每一个元素都与X的每一个元素相对应，不需要乘的记为0即可。最终获得C矩阵如下图。

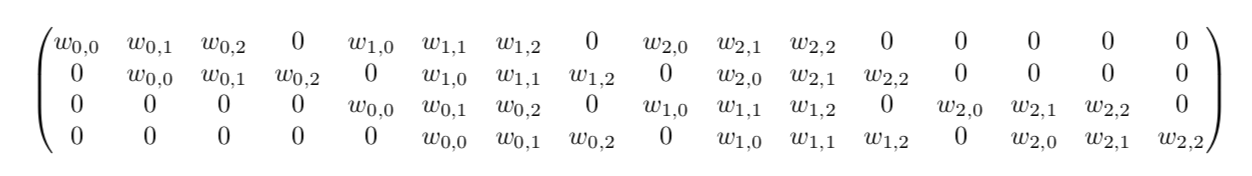
Transposed convolution

我们再来考虑另一个方向，将2x2作为输入转化为4x4，按照卷积步骤，并将C转置。
$X_{16X1}=C_{4X16}^{T}Y_{4X1}$
上述称之为转置卷积。kernel定义卷积和转置卷积，卷积和转置卷积取决于前向和后向运算。对于卷积而言，前向和反向通过 $C和C^T$。对于转置卷积而言，其前向和反向通过 $C^T和(C^T)^T$。我们可以通过直接卷积模拟转置卷积，但通常要向输入添加不少0的行和列，这在运算上不高效。

理解

我们可以这样理解转置卷积，可以把输入看做是一个初始特征卷积后的结果，如上述3x3卷积核在4x4输入卷积获得2x2的结果，应用转置卷积则输出应该是4x4。另外一种理解方式是直接卷积，将2x2的输入卷积成4x4的输出，这里需要0填充，为了保证与卷积相同的连接性模式，kernel第一次计算应该只接受输入的左上角元素，所以填充大小=kernel-1。
关于其他的参数选择，可以查看论文原文卷积与反卷积
git帮助理解的gifConvolution arithmetic
参考反卷积/转置卷积 的理解