第五章动态规划

小结：
不太会动态规划
1.最大连续乘积子串
2. 字符串编辑距离
3. 格子取数问题
4. 交替字符串
5. 最长递增子序列

本章导读

学习一个算法，可分为3个步骤：首先了解算法本身解决什么问题，然后学习它的解决策略，最后了解某些相似算法之间的联系。例如图算法中，

广搜是一层一层往外遍历，寻找最短路径，其策略是采取队列的方法。
最小生成树是最小代价连接所有点，其策略是贪心，比如Prim的策略是贪心+权重队列。
Dijkstra是寻找单源最短路径，其策略是贪心+非负权重队列。
Floyd是多结点对的最短路径，其策略是动态规划。

而贪心和动态规划是有联系的，贪心是“最优子结构+局部最优”，动态规划是“最优独立重叠子结构+全局最优”。一句话理解动态规划，则是枚举所有状态，然后剪枝，寻找最优状态，同时将每一次求解子问题的结果保存在一张“表格”中，以后再遇到重叠的子问题，从表格中保存的状态中查找（俗称记忆化搜索）。

1. 最大连续乘积子串

题目描述

给一个浮点数序列，取最大乘积连续子串的值，例如 -2.5，4，0，3，0.5，8，-1，则取出的最大乘积连续子串为3，0.5，8。也就是说，上述数组中，3 0.5 8这3个数的乘积30.58=12是最大的，而且是连续的。

分析与解法

此最大乘积连续子串与最大乘积子序列不同，请勿混淆，前者子串要求连续，后者子序列(LCS)不要求连续。LCS可以使用动态规划解决

解法一：暴力

两重for循环，时间复杂度O(n^2)

解法二：动态规划

考虑到乘积子序列中有正有负也还可能有0，我们可以把问题简化成这样：数组中找一个子序列，使得它的乘积最大；同时找一个子序列，使得它的乘积最小（负数的情况）。

假设数组为a[]，直接利用动态规划来求解，考虑到可能存在负数的情况，我们用maxend来表示以a[i]结尾的最大连续子串的乘积值，用minend表示以a[i]结尾的最小的子串的乘积值，那么状态转移方程为：

 maxend = max(max(maxend * a[i], minend * a[i]), a[i]);
 minend = min(min(maxend * a[i], minend * a[i]), a[i]);
 初始状态为maxend = minend = a[0]。

参考代码如下：

double MaxProductSubstring(double *a, int length)
{
	double maxEnd = a[0];
	double minEnd = a[0];
	double maxResult = a[0];
	for (int i = 1; i < length; ++i)
	{
		double end1 = maxEnd * a[i], end2 = minEnd * a[i];
		maxEnd = max(max(end1, end2), a[i]);
		minEnd = min(min(end1, end2), a[i]);
		maxResult = max(maxResult, maxEnd);
	}
	return maxResult;
}

动态规划求解的方法一个for循环搞定，所以时间复杂度为O(n)。

2. 字符串编辑距离

题目描述

给定一个源串和目标串，能够对源串进行如下操作：

在给定位置上插入一个字符
替换任意字符
删除任意字符
写一个程序，返回最小操作数，使得对源串进行这些操作后等于目标串，源串和目标串的长度都小于2000。

分析与解法

此问题的常见思路是动态规划，假如令dp[i][j]表示原串S[0…i]和目标串T[0…j]的最短编辑距离，其边界：dp[0][j] = j, dp[i][0] = i，那么我们可以得出状态转移方程：

dp[i][j] = min{
- dp[i-1][j]+1, S[i]不在T[0…j]中
- dp[i-1][j-1] +1/0, S[i]在T[j]
- dp[i][j-1] + 1, S[i]在T[0…j-1]中
  }

接下来，我们重点解释一下上述3个式子的含义

关于dp[i-1][j] + 1, s.t. s[i]不在T[0…j]中的说明
- S[i]没有落在T[0…j]中，即S[i]在中间的某次编辑操作中被删除。因为删除操作没有前后相关性，不妨将其在第一次操作中删除，除首次操作时删除外，后续编辑操作是将长度的i - 1的字符串编辑成长度为j的字符串：即dp[i - 1][j]
- 因此，dp[i][j] = dp[i-1][j] + 1
关于dp[i - 1][j - 1] + 0/1， s.t. s[i] 在T[j]的说明
- 若s[i]经过编辑，最终落在T[j]的位置。
- 则要么s[i] == t[j], s[i]直接落在T[j]：即dp[i-1][j-1];
- 则要么s[i] != t[j]，s[i]落在T[j]后，要将s[i]修改成T[j]，增加一次修改操作：即dp[i-1][j-1]+1
关于dp[i][j-1] + 1, s.t. s[i]在T[0…j-1]中的说明
- 若若s[i]落在了T[1…j-1]的某个位置，不妨认为是k，因为最小编辑步数的定义，那么，在k+1到j-1的字符，必然是通过插入新字符完成的。因为共插入了(j-k)个字符，故编辑次数为(j-k)次。而字符串S[1…i]经过编辑，得到了T[1…k]，编辑次数为dp[i][k]。故： dp[i][j] = dp[i][k] + (j-k)。
- 由于最后的(j-k)次是插入操作，可以讲(j-k)逐次规约到dp[i][k]中。即：dp[i][k]+(j-k)=dp[i][k+1] + (j-k-1) 规约到插入操作为1次，得到 dp[i][k]+(j-k) =dp[i][k+1] + (j-k-1) =dp[i][k+2] + (j-k-2)=… =dp[i][k+(j-k-1)] + (j-k)-(j-k-1) =dp[i][j-1] + 1。

换一个角度，其实就是字符串对齐的思路。例如把字符串“ALGORITHM”，变成“ALTRUISTIC”，那么把相关字符各自对齐后，如下图所示：
在这里插入图片描述
把图中上面的源串S[0…i] = “ALGORITHM”编辑成下面的目标串T[0…j] = “ALTRUISTIC”，我们枚举字符串S和T最后一个字符s[i]、t[j]对应四种情况：（字符-空白）（空白-字符）(字符-字符)（空白-空白）。
由于（空白-空白）是多余的编辑操作。所以，事实上只存在以下3种情况：

下面的目标串空白，即S + 字符X，T + 空白，S变成T，意味着源串要删字符
- dp[i - 1, j] + 1
上面的源串空白，S + 空白，T + 字符，S变成T，最后，在S的最后插入“字符”，意味着源串要添加字符
- dp[i, j - 1] + 1
上面源串中的的字符跟下面目标串中的字符不一样，即S + 字符X，T + 字符Y，S变成T，意味着源串要修改字符
- dp[i - 1, j - 1] + (s[i] == t[j] ? 0 : 1)

//dp[i,j]表示表示源串S[0…i] 和目标串T[0…j] 的最短编辑距离
dp[i, j] = min { dp[i - 1, j] + 1,  dp[i, j - 1] + 1,  dp[i - 1, j - 1] + (s[i] == t[j] ? 0 : 1) }
//分别表示：删除1个，添加1个，替换1个（相同就不用替换）。

3. 格子取数问题???

题目描述
有n*n个格子，每个格子里有正数或者0，从最左上角往最右下角走，只能向下和向右，一共走两次（即从左上角走到右下角走两趟），把所有经过的格子的数加起来，求最大值SUM，且两次如果经过同一个格子，则最后总和SUM中该格子的计数只加一次。
在这里插入图片描述

分析与解法

因为要让两次走下来的路径总和最大，读者可能最初想到的思路可能是让每一次的路径都是最优的，即不顾全局，只看局部，让第一次和第二次的路径都是最优。
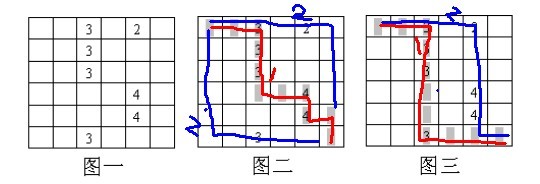
在这里插入图片描述
也就是说，上面图二中的走法太追求每一次最优，所以第一次最优，导致第二次将是很差；而图三第一次虽然不是最优，但保证了第二次不差，所以图三的结果优于图二。由此可知不要只顾局部而贪图一时最优，而丧失了全局最优。

为了方便讨论，我们先对矩阵做一个编号，且以5*5的矩阵为例（给这个矩阵起个名字叫M1）：
M1

0 1 2 3 4

1 2 3 4 5

2 3 4 5 6

3 4 5 6 7

4 5 6 7 8
从左上(0)走到右下(8)共需要走8步（2*5-2）。我们设所走的步数为s。因为限定了只能向右和向下走，因此无论如何走，经过8步后（s = 8)都将走到右下。而DP的状态也是依据所走的步数来记录的。

再来分析一下经过其他s步后所处的位置，根据上面的讨论，可以知道：

经过8步后，一定处于右下角(8)；
那么经过5步后(s = 5)，肯定会处于编号为5的位置；
3步后肯定处于编号为3的位置；
s = 4的时候，处于编号为4的位置，此时对于方格中，共有5（相当于n）个不同的位置，也是所有编号中最多的。

故推广来说，对于n*n的方格，总共需要走2n - 2步，且当s = n - 1时，编号为n个，也是编号数最多的。

如果用DP[s,i,j]来记录2次所走的状态获得的最大值，其中s表示走s步，i和j分别表示在s步后第1趟走的位置和第2趟走的位置。

为了方便描述，再对矩阵做一个编号（给这个矩阵起个名字叫M2）：
M2

0 0 0 0 0

1 1 1 1 1

2 2 2 2 2

3 3 3 3 3

4 4 4 4 4

我们先看M1，在经过6步后，肯定处于M1中编号为6的位置。而M1中共有3个编号为6的，它们分别对应M2中的2 3 4。故对于M2来说，假设第1次经过6步走到了M2中的2，第2次经过6步走到了M2中的4，DP[s,i,j] 则对应 DP[6,2,4]。由于s = 2n - 2,0 <= i <= j <= n，所以这个DP共有O(n^3)个状态。

再来分析一下状态转移，以DP[6,2,3]为例，可以到达DP[6,2,3]的状态包括DP[5,1,2]，DP[5,1,3]，DP[5,2,2]，DP[5,2,3]

下面，我们就来看看这几个状态：DP[5,1,2]，DP[5,1,3]，DP[5,2,2]，DP[5,2,3]，用加粗表示位置DP[5,1,2] DP[5,1,3] DP[5,2,2] DP[5,2,3] （加红表示要达到的状态DP[6,2,3]）

0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

2 3 4 5 6 2 3 4 5 6 2 3 4 5 6 2 3 4 5 6

3 4 5 6 7 3 4 5 6 7 3 4 5 6 7 3 4 5 6 7

4 5 6 7 8 4 5 6 7 8 4 5 6 7 8 4 5 6 7 8

因此：
DP[6,2,3] = Max(DP[5,1,2] ，DP[5,1,3]，DP[5,2,2]，DP[5,2,3]) + 6,2和6,3格子中对应的数值（式一）
上面（式一）所示的这个递推看起来没有涉及：“如果两次经过同一个格子，那么该数只加一次的这个条件”，讨论这个条件需要换一个例子，以DP[6,2,2]为例：DP[6,2,2]可以由DP[5,1,1]，DP[5,1,2]，DP[5,2,2]到达，但由于i = j，也就是2次走到同一个格子，那么数值只能加1次。所以当i = j时，
DP[6,2,2] = Max(DP[5,1,1]，DP[5,1,2]，DP[5,2,2]) + 6,2格子中对应的数值

故，综合上述的（式一），（式二）最后的递推式就是

f(i != j) DP[s, i ,j] = Max(DP[s - 1, i - 1, j - 1], DP[s - 1, i - 1, j], DP[s - 1, i, j - 1], DP[s - 1, i, j]) + W[s,i] + W[s,j] else DP[s, i ,j] = Max(DP[s - 1, i - 1, j - 1], DP[s - 1, i - 1, j], DP[s - 1, i, j]) + W[s,i]

其中W[s,i]表示经过s步后，处于i位置，位置i对应的方格中的数字。下一节我们将根据上述DP方程编码实现。

//copyright@caopengcs 2013
const int N = 202;
const int inf = 1000000000;  //无穷大
int dp[N * 2][N][N];
bool IsValid(int step, int x1, int x2, int n) //判断状态是否合法
{
    int y1 = step - x1, y2 = step - x2;
    return ((x1 >= 0) && (x1 < n) && (x2 >= 0) && (x2 < n) && (y1 >= 0) && (y1 < n) && (y2 >= 0) && (y2 < n));
}

int GetValue(int step, int x1, int x2, int n)  //处理越界 不存在的位置 给负无穷的值
{
    return IsValid(step, x1, x2, n) ? dp[step][x1][x2] : (-inf);
}

//状态表示dp[step][i][j] 并且i <= j, 第step步  两个人分别在第i行和第j行的最大得分 时间复杂度O(n^3) 空间复杂度O(n^3)
int MinPathSum(int a[N][N], int n)
{
    int P = n * 2 - 2; //最终的步数
    int i, j, step;

    //不能到达的位置 设置为负无穷大
    for (i = 0; i < n; ++i)
    {
        for (j = i; j < n; ++j)
        {
            dp[0][i][j] = -inf;
        }
    }
    dp[0][0][0] = a[0][0];

    for (step = 1; step <= P; ++step)
    {
        for (i = 0; i < n; ++i)
        {
            for (j = i; j < n; ++j)
            {
                dp[step][i][j] = -inf;
                if (!IsValid(step, i, j, n))   //非法位置
                {
                    continue;
                }
                //对于合法的位置进行dp
                if (i != j)
                {
                    dp[step][i][j] = max(dp[step][i][j], GetValue(step - 1, i - 1, j - 1, n));
                    dp[step][i][j] = max(dp[step][i][j], GetValue(step - 1, i - 1, j, n));
                    dp[step][i][j] = max(dp[step][i][j], GetValue(step - 1, i, j - 1, n));
                    dp[step][i][j] = max(dp[step][i][j], GetValue(step - 1, i, j, n));
                    dp[step][i][j] += a[i][step - i] + a[j][step - j];  //不在同一个格子，加两个数
                }
                else
                {
                    dp[step][i][j] = max(dp[step][i][j], GetValue(step - 1, i - 1, j - 1, n));
                    dp[step][i][j] = max(dp[step][i][j], GetValue(step - 1, i - 1, j,  n));
                    dp[step][i][j] = max(dp[step][i][j], GetValue(step - 1, i, j,  n));
                    dp[step][i][j] += a[i][step - i]; // 在同一个格子里，只能加一次
                }
            }
        }
    }
    return dp[P][n - 1][n - 1];
}

复杂度分析：状态转移最多需要统计4个变量的情况，看做是O(1)的，共有O(n^{3)个状态，所以总的时间复杂度是O(n}3)的，且dp数组开了N^{3大小，故其空间复杂度亦为O(n}3)。

事实上，空间上可以利用滚动数组优化，由于每一步的递推只跟上1步的情况有关，因此可以循环利用数组，将空间复杂度降为O(n^2)。

即我们在推算dp[step]的时候，只依靠它上一次的状态dp[step - 1]，所以dp数组的第一维，我们只开到2就可以了。即step为奇数时，我们用dp[1][i][j]表示状态，step为偶数我们用dp[0][i][j]表示状态，这样我们只需要O(n^2)的空间，这就是滚动数组的方法。滚动数组写起来并不复杂，只需要对上面的代码稍作修改即可，感兴趣的读者可以自己写代码实现下。

4. 交替字符串

题目描述
输入三个字符串s1、s2和s3，判断第三个字符串s3是否由前两个字符串s1和s2交错而成，即不改变s1和s2中各个字符原有的相对顺序，例如当s1 = “aabcc”，s2 = “dbbca”，s3 = “aadbbcbcac”时，则输出true，但如果s3=“accabdbbca”，则输出false。

分析与解法

此题不能简单的排序，因为一旦排序，便改变了s1或s2中各个字符原始的相对顺序，既然不能排序，咱们可以考虑下用动态规划的方法，令dp[i][j]代表s3[0…i+j-1]是否由s1[0…i-1]和s2[0…j-1]的字符组成

如果s1当前字符（即s1[i-1]）等于s3当前字符（即s3[i+j-1]），而且dp[i-1][j]为真，那么可以取s1当前字符而忽略s2的情况，dp[i][j]返回真；
如果s2当前字符等于s3当前字符，并且dp[i][j-1]为真，那么可以取s2而忽略s1的情况，dp[i][j]返回真，其它情况，dp[i][j]返回假

public boolean IsInterleave(String s1, String 2, String 3){
	int n = s1.length(), m = s2.length(), s = s3.length();

	//如果长度不一致，则s3不可能由s1和s2交错组成
	if (n + m != s)
		return false;

	boolean[][]dp = new boolean[n + 1][m + 1];

	//在初始化边界时，我们认为空串可以由空串组成，因此dp[0][0]赋值为true。
	dp[0][0] = true;

	for (int i = 0; i < n + 1; i++){
		for (int j = 0; j < m + 1; j++){
			if ( dp[i][j] || (i - 1 >= 0 && dp[i - 1][j] == true &&
				//取s1字符
				s1.charAT(i - 1) == s3.charAT(i + j - 1)) ||

				(j - 1 >= 0 && dp[i][j - 1] == true &&
				//取s2字符
				s2.charAT(j - 1) == s3.charAT(i + j - 1)) )

				dp[i][j] = true;
			else
				dp[i][j] = false;
		}
	}
	return dp[n][m]
}

5. 最长递增子序列

题目描述
给定一个长度为N的数组a0,a1,a2…,an-1，找出一个最长的单调递增子序列（注：递增的意思是对于任意的i<j，都满足ai<aj，此外子序列的意思是不要求连续，顺序不乱即可）。例如：给定一个长度为6的数组A{5， 6， 7， 1， 2， 8}，则其最长的单调递增子序列为{5，6，7，8}，长度为4。

分析与解法

解法一：转换为最长公共子序列问题

比如原数组为
A{5， 6， 7， 1， 2， 8}，
当我们对这个数组进行排序后，排序后的数组为：
A‘{1， 2， 5， 6， 7， 8}。

然后想求数组A的最长递增子序列，其实就是求数组A与它的排序数组A‘的最长公共子序列，原因是原数组A的子序列顺序保持不变，而且排序后A‘本身就是递增的，这样，就保证了两序列的最长公共子序列的递增特性。

如此，若想求数组A的最长递增子序列，其实就是求数组A与它的排序数组A‘的最长公共子序列。

解法二：动态规划

定义dp[i]为以ai为末尾的最长递增子序列的长度，故以ai结尾的递增子序列

要么是只包含ai的子序列
要么是在满足j<i并且aj<ai的以ai为结尾的递增子序列末尾，追加上ai后得到的子序列

int n;
int a[n];

int dp[n];

void lis()
{
	int res = 0;
	int i;
	for (i = 0; i < n; i++)
	{
		dp[i] = (dp[i] > dp[i + 1] )? dp[i]:dp[i + 1];
	}
	res = (res > dp[i])?res:dp[i];
	printf("%d\n,res");
}

编程之法：面试和算法心得 - 动态规划

第五章动态规划

本章导读

1. 最大连续乘积子串

题目描述

分析与解法

解法一：暴力

解法二：动态规划

2. 字符串编辑距离

题目描述

分析与解法

3. 格子取数问题???

分析与解法

4. 交替字符串

分析与解法

5. 最长递增子序列

分析与解法

解法一：转换为最长公共子序列问题

解法二：动态规划

猜你喜欢

编程之法：面试和算法心得 - 动态规划

第五章 动态规划

本章导读

1. 最大连续乘积子串

题目描述

分析与解法

解法一：暴力

解法二：动态规划

2. 字符串编辑距离

题目描述

分析与解法

3. 格子取数问题???

分析与解法

4. 交替字符串

分析与解法

5. 最长递增子序列

分析与解法

解法一：转换为最长公共子序列问题

解法二：动态规划

猜你喜欢

第五章动态规划