K-Means算法+Spark MLlib代码Demo

引言

我们知道训练样本没有标注的情况，其具体模型称为“无监督学习”，其作用就是要从对原始数据的探索中提取出一定的规律。在无监督学习任务中研究最多、应用最广的就是“聚类”。

在聚类中，我们按照某种特定标准（如距离准则）把数据进行分割，这样每个数据样本就会属于某个部分，称为类簇。也就是说由聚类所生成的簇是一组数据对象的集合，这些对象与同一个簇中的对象彼此相似，与其他簇中的对象相异，这大概就像“物以类聚”。类簇相当于类别，只不过其真实的类别对聚类算法事先是未知的。

聚类算法被应用于许多领域，这些领域通常要求找出特定数据中的“自然关联”。比如，在电子商务上，通过分组聚类出具有相似浏览行为的客户，并分析客户的共同特征，可以更好的帮助电子商务的用户了解自己的客户，向客户提供更合适的服务；聚类也能用于在网上进行文档归类来修复信息，等等。

聚类模型有很多种，从简单到复杂都有，其中k-均值（K-Means）是最简单的聚类算法之一，但也非常有效，简单通常也意味着相对容易理解和扩展，接下来就一起来学一下吧！

一、K-Means算法

1.1 基本思想

K-Means，即k均值算法，是数据挖掘领域中一种常用的聚类方法。其基本思想很简单，就是对于给定的样本集，按照样本之间的距离大小，将样本集划分为k个簇，让簇内的点尽量紧密的连在一起，而让簇间的距离尽量大。

1.2 算法步骤

(1) 将一系列样本分割成k个不同的类簇，最开始随机给定k个簇中心点（初始质心）。

(2) 按照最近距离原则将样本点分配到最近的质心。

(3) 之后按照平均法计算新的质心位置。

(4) 不断迭代更新(也就是重复以上步骤)各个质心的值，直至满足结束条件为止。

（结束条件：比如迭代达到设置的最大迭代次数则结束，或者迭代直到k个质心向量都没有发生变化的时候则结束）

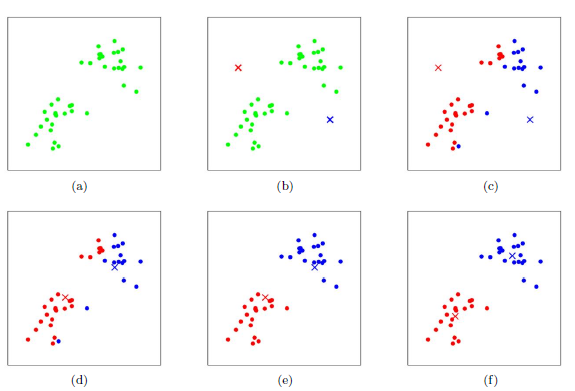
如图(a)为初始的数据集，在这里我们假设k=2，即要分割成两个类簇。

在图(b)中，随机选择了两个类簇所对应的初始质心（红色×和蓝色×），分别求样本中所有点到这两个质心的距离。

如图(c)所示，由最近距离作为依据标记每个样本的类簇（与蓝色×距离近的标为蓝色类簇，与红色×距离近的标为红色类簇），这就是所有样本点经过第一轮迭代后得到的类簇。

接着就是计算得到新的质心，在图(d)中，可以看到红蓝两个质心位置已经发生变化。

图(e)和图(f)即为迭代更新质心这个过程。

1.3 距离度量

按照上述可知，K-Means算法中关于距离的计算是很关键的一点。我们需要选择一种距离公式来确定样本点与质心的距离，其中很常用且比较直观的就是欧氏距离。欧氏距离，即欧几里得距离（Euclidean distance）表示为空间中两个点的真实距离。

二维空间中假设两点分别为 $(x_{1},y_{1})$ ， $(x_{2},y_{2})$ ，那么其两点间的欧氏距离公式为：

$\rho =\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$

三维空间中假设两点分别为 $(x_{1},y_{1},z_{1})$ ， $(x_{2},y_{2},z_{2})$ ，那么其两点间的欧氏距离公式为：

$\rho =\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}$

可推到n维空间的欧氏距离公式如下（此时两个点分别为 $(x_{1},x_{2},...,x_{n})$ 和 $(y_{1},y_{2},...,y_{n})$ ）：

$d(x,y) =\sqrt{(x_{1}-y_{1})^{2}+(x_{2}-y_{2})^{2}+...+(x_{n}-y_{n})^{2}}=\sqrt{\sum_{i=1}^{n}(x_{i}-y_{i})^{2}}$

（常见的数学距离，还有曼哈顿距离、切比雪夫距离、闵式距离等等，可自行百度了解一下）

1.4 算法定义

给定样本集 $D=\left \{ x_{1},x_{2},...,x_{m} \right \}$ ，将样本分为k个类簇，得到簇划分 $C= \left \{ C_{1},C_{2},...,C_{k}\right \}$ 。算法目的就是最小化所有类簇中的平方误差，使用平方误差作为目标函数 $E$ 公式如下：

$E=\sum_{i=1}^{k}\sum_{j\in C_{i}}^{ }(x^{(j)}-\mu _{i})^{2}$

其中 $\mu _{i}=\frac{1}{\left |C_{i} \right |}\sum _{x\in c_{k}}x$ 是簇 $C_{i}$ 的均值向量（也就是质心的位置，会迭代更新）。 $E$ 刻画了簇内样本围绕簇均值向量的紧密程度，其值越小则簇内样本相似度越高。最终我们要对上式求得最优解，按照距离最小原则，就是让目标函数尽可能的小，做法就是对 $E$ 求偏导数，使偏导数等于0，就能求出最优质心。

1.5 最优k值确定

如上所述，最开始划分为几个类簇（k值）是可以人为设置的。但是毕竟人算不如天算，选择一个恰当的k值对于最终的聚类效果肯定会有提升的，并不是k值越大越好。因此有两种方法可以用于选择最优k值：手肘法、轮廓系数法。详情点击此处。

1.6 案例

（源自西瓜书《机器学习——周志华》）

先献上西瓜数据集：

如上编号 $i$ 的样本为 $x_{i}$ ，其为一个包含“密度”和“含糖率”两个属性值（或者特征）的二维向量。

算法流程：

(1) 假定我们要划分的类簇数k=3，算法开始时随机选取三个样本 $x_{6}$ ， $x_{12}$ ， $x_{27}$ 作为初始质心，即

$\mu _{1}=(0.403,0.237)$ ， $\mu _{2}=(0.343,0.099)$ ， $\mu _{3}=(0.532,0.472)$

对应三个簇分别为 $C_{1}$ ， $C_{2}$ ， $C_{3}$ 。

(2) 计算所有样本点与各个质心之间的距离，以样本点 $x_{1}=(0.697,0.460)$ 为例进行考察：

按照欧拉距离公式，计算 $x_{1}$ 与 $\mu _{1}$ 的距离为： $\sqrt{(0.697-0.403)^{2}+(0.460-0.237)^{2}}=0.369$

同理可得 $x_{1}$ 与 $\mu _{2}$ 的距离为0.506； $x_{1}$ 与 $\mu _{3}$ 的距离为0.166。

(3) 根据最小距离原则，将样本点划入距离最近的质心所在的那个簇。如上 $0.166<0.369<0.506$ ，也就是 $x_{1}$ 与 $\mu _{3}$ 的距离是最近的，则将 $x_{1}$ 划分到簇 $C_{3}$ 中。类似的，对数据集中的所有样本都考察一遍，可得当前簇划分为：

$C_{1}=\left \{ x_{5},x_{6},x_{7},x_{8},x_{9},x_{10}, x_{13},x_{14},x_{15},x_{17},x_{18},x_{19},x_{20},x_{23}\right \}$

$C_{2}=\left \{ x_{11},x_{12},x_{16}\right \}$

$C_{3}=\left \{ x_{1},x_{2},x_{3},x_{4},x_{21},x_{22}, x_{24},x_{25},x_{26},x_{27},x_{28},x_{29},x_{30}\right \}$

(4) 从 $C_{1}$ ， $C_{2}$ ， $C_{3}$ 分别求出新的质心位置：

求质心位置，其实就是求簇类中的均指向量（均值向量就是随机变量的数学期望）。例如求 $C_{2}$ 中的质心：由上可知 $C_{2}$ 中有三个样本点 $x_{11}=(0.245,0.057)$ ， $x_{12}=(0.343,0.099)$ ， $x_{16}=(0.593,0.042)$ ，那么其质心的位置为

${\mu _{2}}'=(\frac{0.245+0.343+0.593}{3},\frac{0.057+0.099+0.042}{3})=(0.394,0.066)$

同理分别可得 $C_{1}$ ， $C_{3}$ 对应的质心 ${\mu _{1}}'=(0.473,0.214)$ ， ${\mu _{3}}'=(0.623,0.388)$

(5) 重复上述过程，迭代更新质心的位置。最后迭代到了第五轮的时候，可发现产生的结果和第四次的迭代结果一致，于是算法停止，得到最终的簇划分。

大概过程如下图所示：

二、Spark MLlib K-Means

2.1 案例代码及输出结果

根据上面的西瓜案例，数据如下：

0.697 0.460
0.774 0.376
0.634 0.264
0.608 0.318
0.556 0.215
0.403 0.237
0.481 0.149
0.437 0.211
0.666 0.091
0.243 0.267
0.245 0.057
0.343 0.099
0.639 0.161
0.657 0.198
0.360 0.370
0.593 0.042
0.719 0.103
0.359 0.188
0.339 0.241
0.282 0.257
0.748 0.232
0.714 0.346
0.483 0.312
0.478 0.437
0.525 0.369
0.751 0.489
0.532 0.472
0.473 0.376
0.725 0.445
0.446 0.459

代码如下：

package sparkMllib.clustering
import org.apache.log4j.{Level, Logger}
import org.apache.spark.mllib.clustering.KMeans
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.{SparkConf, SparkContext}

object KMeansTest {
  def main(args: Array[String]): Unit = {
    Logger.getLogger("org.apache.spark").setLevel(Level.WARN)
    Logger.getLogger("org.apache.jetty.server").setLevel(Level.OFF)

    //处理数据，转换为向量
    val conf=new SparkConf().setMaster("local").setAppName("KmeansTest")
    val sc=new SparkContext(conf)
    val data = sc.textFile("E:\\test\\sample_kmeans_data.txt")
    val parsedData = data.map(line => {
      Vectors.dense(line.split(" ").map(_.toDouble))
    })

    //k=3：设置分为3个簇；maxIterations=10：设置最大迭代次数；然后传入train方法训练得到模型
    val k=3
    val maxIterations=10
    val model = KMeans.train(parsedData,k,maxIterations)

    //输出最终3个类簇的质心
    println("Cluster centers:")
    for (c<-model.clusterCenters){
      println(c.toString)
    }

    //使用模型测试单点数据
    println(" ")
    val v1 = Vectors.dense("0.222 0.444".split(" ").map(_.toDouble))
    val v2 = Vectors.dense("0.333 0.222".split(" ").map(_.toDouble))
    val v3 = Vectors.dense("0.666 0.111".split(" ").map(_.toDouble))
    val v4 = Vectors.dense("0.111 0.666".split(" ").map(_.toDouble))
    println(s"v1=(${v1.apply(0)},${v1.apply(1)}) is belong to cluster:"+model.predict(v1))
    println(s"v2=(${v2.apply(0)},${v2.apply(1)}) is belong to cluster:"+model.predict(v2))
    println(s"v3=(${v3.apply(0)},${v3.apply(1)}) is belong to cluster:"+model.predict(v3))
    println(s"v4=(${v4.apply(0)},${v4.apply(1)}) is belong to cluster:"+model.predict(v4))
  }

}

输出结果：

代码中输入了v1、v2、v3、v4四个测试点，让训练得到的模型预测这四个点分别属于哪个类簇。输出的0、1、2代表三个类簇的编号，从结果可以看出v1和v4同属于“0”这个类簇。在此说明一下，每次运行后得到的结果可能会不一样，因为系统在算法运行开始时，会随机选取初始质心，每次选取的初始质心都会不一样，聚类结果也会有所不同。但是可以确认的一点就是，归为同一类簇的对象，都可认为它们彼此相似，具有某些相同的特征属性。

2.2 评估模型

对于K-Means模型，Spark MLlib内部评估指标为簇内误差平方之和WSSSE（Within Set Sum of Squared Errors）。毫无疑问，该值越小表明类簇内部的样本距离越接近，不同类簇的样本相对较远。计算该值代码如下：

    //使用误差平方之和来评估模型
    val cost = model.computeCost(parsedData)
    println("Within Set Sum of Squared Errors ="+cost)

2.3 性能调优

类似分类和回归模型，我们可以应用交叉验证来选择模型最优的k值。这和监督学习的过程一样。需要将数据集分割为训练集和测试集，在训练集上训练模型，在测试集上评估感兴趣的指标的性能。如下代码将数据集划分得到训练集（80%）和测试集（20%），并使用如上的WSSSE作为评估指标：

    //数据分为训练数据(80%)，测试数据(20%)
    val splits = parsedData.randomSplit(Array(0.8,0.2),seed = 11L)
    val trainingData = splits(0)     //训练数据
    val testingData = splits(1)      //测试数据

    val costs = Seq(1, 2, 3, 4, 5, 6, 7, 8, 9, 10).map {
      k => (k, KMeans.train(trainingData, k, 10).computeCost(testingData))
    }
    costs.foreach{case (k,cost)=>{println(f"WSSSE for k=$k is $cost%2.3f")}}

输出结果：

绘制成柱状图，如下（横坐标为k，纵坐标为WSSSE）：

从柱状图可以看出，WSSSE随着k的增大持续减小，但是达到某个值后，变化趋于平缓的状态，这时的k通常就为最优的k值,所以如上的最优k值可取6左右。

需要说明的是，模型计算得到的类簇需要人工解释（比如分在某个类簇的瓜很甜，另外一个类簇相对就没那么甜），尽管较大的k值从数学角度来说，可以得到更优的解，但是实际上，类簇太多反而会变得难以理解和解释。

三、总结

最后针对K-Means算法做一个优点和缺点的总结：

主要优点

原理比较简单，实现也是很容易，收敛速度快。

聚类效果较优。

算法的可解释度比较强。

主要需要调参的参数仅仅是簇数k。

主要缺点

K值的选取不好把握

对于不是凸的数据集比较难收敛。

如果各隐含类别的数据不平衡，比如各隐含类别的数据量严重失衡，或者各隐含类别的方差不同，则聚类效果不佳。

采用迭代方法，得到的结果只是局部最优。

对噪音和异常点比较的敏感。

引用及参考：

[1] 《机器学习》周志华著

[2] 《Spark机器学习》 [南非]Nick Pentreath著

[3] https://www.cnblogs.com/pinard/p/6164214.html

[4] https://blog.csdn.net/loveliuzz/article/details/78783773

[5] https://www.cnblogs.com/ksWorld/p/6905836.html

（欢迎转载，转载请注明出处）