Introduction

您曾经使用过具有超过一千个功能的数据集吗？ 超过50,000个功能怎么样？ 我有，让我告诉你这是一项非常具有挑战性的任务，特别是如果你不知道从哪里开始！ 拥有大量变量既是恩惠，也是诅咒。 我们有大量的数据用于分析，这很棒，但由于尺寸的原因，它具有挑战性。

在微观层面分析每个变量是不可行的。 我们可能需要几天或几个月才能进行任何有意义的分析，我们将为您的业务损失大量的时间和金钱！ 更不用说这将需要的计算能力。 我们需要一种更好的方法来处理高维数据，以便我们能够快速从中提取模式和见解。 那么我们如何处理这样的数据集呢？

当然，使用降维技术。 您可以使用此概念来减少数据集中的要素数量，而不必丢失太多信息并保持（或改进）模型的性能。 正如您将在本文中看到的，这是处理大型数据集的一种非常强大的方法。

这是可以在实际场景中使用的各种降维技术的综合指南。 在深入介绍我所涵盖的12种不同技术之前，我们将首先了解这个概念是什么以及为什么要使用它。 每种技术都有自己的Python实现，让你熟悉它。

Table of Contents

• 1什么是降维？
• 2为什么需要降维？
• 3种常见的降维技术
  3.1缺失值比率
  3.2低方差滤波器
  3.3高相关滤波器
  3.4随机森林
  3.5向后特征消除
  3.6前向特征选择
  3.7因子分析
  3.8主成分分析
  3.9独立分量分析
  3.10基于投影的方法
  3.11 t分布式随机邻域嵌入（t-SNE）
  3.12 UMAP
• 4种各种降维技术的应用

1. What is Dimensionality Reduction?

我们每天都在生成大量数据。 事实上，世界上90％的数据都是在过去的3到4年中产生的！ 这些数字真的令人难以置信。 以下是收集的数据类型的一些示例：

• Facebook收集您喜欢，分享，发布，访问的地点，您喜欢的餐馆等的数据。
• 您的智能手机应用程序收集了大量有关您的个人信息
• 亚马逊收集您在其网站上购买，查看，点击等内容的数据
• 赌场跟踪每位客户的每一步行动

随着数据生成和收集的不断增加，可视化和绘制推理变得越来越具有挑战性。 进行可视化的最常见方法之一是通过图表。 假设我们有2个变量，Age和Height。 我们可以使用Age和Height之间的散点图或线图，并轻松地将它们的关系可视化：

现在考虑我们有100个变量（p = 100）的情况。 在这种情况下，我们可以有100（100-1）/ 2 = 5000个不同的图。 将它们分别可视化是没有多大意义的，对吧？ 在我们有大量变量的情况下，最好选择这些变量的一个子集（p << 100），它捕获与原始变量集一样多的信息。

让我们用一个简单的例子来理解这一点。 考虑下面的图像：

这里我们有类似物体的重量，单位为Kg（X1）和磅（X2）。 如果我们使用这两个变量，它们将传达类似的信息。 因此，仅使用一个变量是有意义的。 我们可以将数据从2D（X1和X2）转换为1D（Y1），如下所示：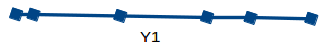

类似地，我们可以将数据的p维度减少为k维度的子集（k << n）。 这称为降维。

2. Why is Dimensionality Reduction required?

以下是将维数减少应用于数据集的一些好处：

• 随着尺寸数量的减少，存储数据所需的空间会减少
• 更少的尺寸可以减少计算/培训时间
• 当我们有大尺寸时，某些算法表现不佳。因此，需要减少这些维度才能使算法有用
• 它通过删除冗余功能来处理多重共线性。例如，你有两个变量 - “在几分钟内在跑步机上花费的时间”和“燃烧的卡路里”。这些变量高度相关，因为您在跑步机上花费的时间越多，您燃烧的卡路里就越多。因此，存储两者都没有意义，因为只有其中一个可以满足您的需求
• 它有助于可视化数据。如前所述，很难以更高的维度显示数据，因此将我们的空间缩小到2D或3D可以让我们更清晰地绘制和观察模式

是时候深入了解本文的关键 - 各种降维技术！我们将使用AV的实践问题数据集：Big Mart Sales III（在此链接上注册并下载来自数据部分的数据集）。

3. Common Dimensionality Reduction Techniques

维度降低可以通过两种不同的方式完成：

• 仅保留原始数据集中最相关的变量（此技术称为特征选择）
• 通过查找一组较小的新变量，每个变量都是输入变量的组合，包含与输入变量基本相同的信息（此技术称为降维）

我们现在将介绍各种降维技术以及如何在Python中实现它们。

3.1 Missing Value Ratio

假设您有一个数据集。 你的第一步是什么？ 在构建模型之前，您自然希望首先探索数据。 在浏览数据时，您会发现数据集中存在一些缺失值。 怎么办？ 您将尝试找出这些缺失值的原因，然后将它们归入或完全删除具有缺失值的变量（使用适当的方法）。

如果我们有太多的缺失值（比如说超过50％）怎么办？ 我们应该归咎于缺失值还是丢弃变量？ 我宁愿放弃变量，因为它没有太多的信息。 然而，这不是一成不变的。 我们可以设置一个阈值，如果任何变量中缺失值的百分比大于该阈值，我们将删除该变量。

我们在Python中实现这种方法。

# import required libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

首先，让我们加载数据：

# read the data
train=pd.read_csv("Train_UWu5bXk.csv")

注意：应在读取数据时添加文件的路径。

现在，我们将检查每个变量中缺失值的百分比。 我们可以使用.isnull（）。sum（）来计算它。

# checking the percentage of missing values in each variable
train.isnull().sum()/len(train)*100

正如您在上表中所看到的，没有太多的缺失值（实际上只有2个变量具有它们）。 我们可以使用适当的方法来估算值，或者我们可以设置阈值，比如20％，并删除具有超过20％缺失值的变量。 让我们看看如何在Python中完成此操作：

# saving missing values in a variable
a = train.isnull().sum()/len(train)*100
# saving column names in a variable
variables = train.columns
variable = [ ]
for i in range(0,12):
    if a[i]<=20:   #setting the threshold as 20%
        variable.append(variables[i])

因此，要使用的变量存储在“变量”中，该变量仅包含缺失值小于20％的那些特征。

3.2 Low Variance Filter

考虑我们的数据集中的一个变量，其中所有观察值都具有相同的值，例如1.如果我们使用此变量，您认为它可以改进我们将构建的模型吗？ 答案是否定的，因为这个变量的方差为零。

因此，我们需要计算给出的每个变量的方差。 然后删除与我们的数据集中的其他变量相比具有低方差的变量。 如上所述，这样做的原因是方差较小的变量不会影响目标变量。

让我们首先使用已知Item_Weight观察值的中值来估算Item_Weight列中的缺失值。 对于Outlet_Size列，我们将使用已知Outlet_Size值的模式来计算缺失值：

train['Item_Weight'].fillna(train['Item_Weight'].median(), inplace=True)
train['Outlet_Size'].fillna(train['Outlet_Size'].mode()[0], inplace=True)

让我们检查是否已填写所有缺失值：

train.isnull().sum()/len(train)*100

Voila! 瞧！ 我们都准备好了。 现在让我们计算所有数值变量的方差。

train.var()

如上面的输出所示，与其他变量相比，Item_Visibility的方差非常小。 我们可以安全地删除此列。 这就是我们应用低方差滤波器的方法。 我们在Python中实现这个：

numeric = train[['Item_Weight', 'Item_Visibility', 'Item_MRP', 'Outlet_Establishment_Year']]
var = numeric.var()
numeric = numeric.columns
variable = [ ]
for i in range(0,len(var)):
    if var[i]>=10:   #setting the threshold as 10%
       variable.append(numeric[i+1])

上面的代码为我们提供了方差大于10的变量列表。

3.3 High Correlation filter

两个变量之间的高度相关意味着它们具有相似的趋势并且可能携带类似的信息。 这可以大大降低某些模型的性能（例如线性和逻辑回归模型）。 我们可以计算出本质上是数值的独立数值变量之间的相关性。 如果相关系数超过某个阈值，我们可以删除其中一个变量（丢弃一个变量是非常主观的，并且应该始终记住保持域名）。

作为一般准则，我们应该保留那些与目标变量显示相当或高相关性的变量。

让我们在Python中执行相关计算。 我们将首先删除因变量（Item_Outlet_Sales）并将剩余的变量保存在新的数据帧（df）中。

df=train.drop('Item_Outlet_Sales', 1)
df.corr()

太棒了，我们的数据集中没有任何具有高相关性的变量。 通常，如果一对变量之间的相关性大于0.5-0.6，我们应该认真考虑丢弃其中一个变量。

3.4 Random Forest

随机森林是最广泛使用的特征选择算法之一。 它具有内置的功能重要性，因此您无需单独编程。 这有助于我们选择较小的要素子集。

我们需要通过应用一个热编码将数据转换为数字形式，因为随机森林（Scikit-Learn Implementation）仅采用数字输入。 让我们也删除ID变量（Item_Identifier和Outlet_Identifier），因为这些只是唯一的数字，对我们来说当前并不重要。

from sklearn.ensemble import RandomForestRegressor
df=df.drop(['Item_Identifier', 'Outlet_Identifier'], axis=1)
model = RandomForestRegressor(random_state=1, max_depth=10)
df=pd.get_dummies(df)
model.fit(df,train.Item_Outlet_Sales)

拟合模型后，绘制要素重要性图：

features = df.columns
importances = model.feature_importances_
indices = np.argsort(importances)[-9:]  # top 10 features
plt.title('Feature Importances')
plt.barh(range(len(indices)), importances[indices], color='b', align='center')
plt.yticks(range(len(indices)), [features[i] for i in indices])
plt.xlabel('Relative Importance')
plt.show()

基于上图，我们可以手动选择最顶层的特征来减少数据集中的维度。 另外，我们可以使用sklearn的SelectFromModel来实现。 它根据权重的重要性选择要素。

from sklearn.feature_selection import SelectFromModel
feature = SelectFromModel(model)
Fit = feature.fit_transform(df, train.Item_Outlet_Sales)

3.5 Backward Feature Elimination

按照以下步骤来理解和使用“向后特征消除”技术：

• 我们首先获取数据集中存在的所有n个变量，并使用它们训练模型
• 然后我们计算模型的性能
• 现在，我们在消除每个变量（n次）后计算模型的性能，即我们每次都丢弃一个变量并在剩余的n-1个变量上训练模型
• 我们确定其移除产生模型性能最小（或没有）变化的变量，然后删除该变量
• 重复此过程，直到不能删除任何变量

在构建线性回归或Logistic回归模型时，可以使用此方法。 我们来看看它的Python实现：

from sklearn.linear_model import LinearRegression
from sklearn.feature_selection import RFE
from sklearn import datasets
lreg = LinearRegression()
rfe = RFE(lreg, 10)
rfe = rfe.fit_transform(df, train.Item_Outlet_Sales)

我们需要指定算法和要选择的特征数量，然后我们返回从后向特征消除中获得的变量列表。 我们还可以使用“rfe.ranking_”命令检查变量的排名。

3.6 Forward Feature Selection

这是我们在上面看到的向后特征消除的相反过程。 我们尝试找到改善模型性能的最佳功能，而不是消除功能。 该技术的工作原理如下：

• 我们从一个功能开始。 基本上，我们分别使用每个特征训练模型n次
• 选择性能最佳的变量作为起始变量
• 然后我们重复这个过程并一次添加一个变量。 保留产生最高性能增长的变量
• 我们重复这个过程，直到模型的性能没有显着改善

让我们用Python实现它：

from sklearn.feature_selection import f_regression
ffs = f_regression(df,train.Item_Outlet_Sales )

这将返回一个数组，其中包含变量的F值和与每个F值对应的p值。 请参阅此链接以了解有关F值的更多信息。 为了我们的目的，我们将选择F值大于10的变量：

variable = [ ]
for i in range(0,len(df.columns)-1):
    if ffs[0][i] >=10:
       variable.append(df.columns[i])

这为我们提供了基于前向特征选择算法的最大变量。

注意：后向特征消除和前向特征选择都很耗时且计算量很大。它们实际上仅用于具有少量输入变量的数据集。

到目前为止我们看到的技术通常在我们的数据集中没有大量变量时使用。这些或多或少的特征选择技术。在接下来的部分中，我们将使用Fashion MNIST数据集，该数据集由属于不同类型服装的图像组成，例如， T恤，裤子，包等。数据集可以从“识别服装”实践问题下载。

该数据集共有70,000张图像，其中60,000张在训练集中，其余10,000张是测试图像。对于本文的范围，我们将仅处理培训图像。列车文件采用zip格式。解压缩zip文件后，您将获得一个.csv文件和一个包含这60,000张图像的训练文件夹。每个图像的相应标签可以在’train.csv’文件中找到。

3.7 Factor Analysis

假设我们有两个变量：收入和教育。 这些变量可能具有高度相关性，因为具有较高教育水平的人往往具有显着较高的收入，反之亦然。

在因子分析技术中，变量按其相关性分组，即，特定组中的所有变量之间将具有高相关性，但与其他组的变量的相关性低。 在这里，每个组都被称为一个因素。 与数据的原始尺寸相比，这些因素的数量很少。 但是，这些因素很难观察到。

让我们先读入火车文件夹中包含的所有图像：

import pandas as pd
import numpy as np
from glob import glob
import cv2
images = [cv2.imread(file) for file in glob('train/*.png')]

注意：您必须使用train文件夹的路径替换glob函数内的路径。

现在我们将这些图像转换为numpy数组格式，以便我们可以执行数学运算并绘制图像。

images = np.array(images)
images.shape

(60000, 28, 28, 3)

如上所示，它是一个三维数组。 我们必须将它转换为一维，因为所有即将到来的技术只需要一维输入。 为此，我们需要展平图像：

image = []
for i in range(0,60000):
    img = images[i].flatten()
    image.append(img)
image = np.array(image)

现在让我们创建一个数据框，其中包含每个图像中每个像素的像素值，以及它们对应的标签（对于标签，我们将使用train.csv文件）。

train = pd.read_csv("train.csv")     # Give the complete path of your train.csv file
feat_cols = [ 'pixel'+str(i) for i in range(image.shape[1]) ]
df = pd.DataFrame(image,columns=feat_cols)
df['label'] = train['label']

现在我们将使用因子分析来分解数据集：

from sklearn.decomposition import FactorAnalysis
FA = FactorAnalysis(n_components = 3).fit_transform(df[feat_cols].values)

这里，n_components将决定转换数据中的因子数量。 转换数据后，是时候可视化结果了：

%matplotlib inline
import matplotlib.pyplot as plt
plt.figure(figsize=(12,8))
plt.title('Factor Analysis Components')
plt.scatter(FA[:,0], FA[:,1])
plt.scatter(FA[:,1], FA[:,2])
plt.scatter(FA[:,2],FA[:,0])

看起来很神奇，不是吗？ 我们可以在上图中看到所有不同的因素。 这里，x轴和y轴表示分解因子的值。 正如我前面提到的，很难单独观察这些因素，但我们已经能够成功地减少数据的维度。

3.8 Principal Component Analysis (PCA)

PCA是一种技术，可以帮助我们从现有的大量变量中提取一组新的变量。 这些新提取的变量称为主成分。 您可以参考这篇文章来了解有关PCA的更多信息。 为了便于您快速参考，以下是您在进一步处理之前应该了解的关于PCA的一些要点：

• 主成分是原始变量的线性组合
• 以第一主成分解释数据集中的最大方差的方式提取主成分
• 第二主成分试图解释数据集中的剩余方差，并与第一主成分不相关
• 第三主成分试图解释前两个主成分无法解释的方差等

在进一步移动之前，我们将从我们的数据集中随机绘制一些图像：

rndperm = np.random.permutation(df.shape[0])
plt.gray()
fig = plt.figure(figsize=(20,10))
for i in range(0,15):
    ax = fig.add_subplot(3,5,i+1)
    ax.matshow(df.loc[rndperm[i],feat_cols].values.reshape((28,28*3)).astype(float))

让我们使用Python实现PCA并转换数据集：

from sklearn.decomposition import PCA
pca = PCA(n_components=4)
pca_result = pca.fit_transform(df[feat_cols].values)

在这种情况下，n_components将决定转换数据中的主要组件的数量。 让我们看一下使用这4个组件解释了多少差异。 我们将使用explain_variance_ratio_来计算相同的内容。

plt.plot(range(4), pca.explained_variance_ratio_)
plt.plot(range(4), np.cumsum(pca.explained_variance_ratio_))
plt.title("Component-wise and Cumulative Explained Variance")

在上图中，蓝线表示按成分说明的方差，而橙线表示累积解释的方差。 我们只使用四个组件就可以解释数据集中大约60％的变化。现在让我们尝试可视化每个分解的组件：

import seaborn as sns
plt.style.use('fivethirtyeight')
fig, axarr = plt.subplots(2, 2, figsize=(12, 8))
sns.heatmap(pca.components_[0, :].reshape(28, 84), ax=axarr[0][0], cmap='gray_r')
sns.heatmap(pca.components_[1, :].reshape(28, 84), ax=axarr[0][1], cmap='gray_r')
sns.heatmap(pca.components_[2, :].reshape(28, 84), ax=axarr[1][0], cmap='gray_r')
sns.heatmap(pca.components_[3, :].reshape(28, 84), ax=axarr[1][1], cmap='gray_r')
axarr[0][0].set_title(
"{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[0]*100),
fontsize=12
)
axarr[0][1].set_title(
"{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[1]*100),
fontsize=12
)
axarr[1][0].set_title(
"{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[2]*100),
fontsize=12
)
axarr[1][1].set_title(
"{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[3]*100),
fontsize=12
)
axarr[0][0].set_aspect('equal')
axarr[0][1].set_aspect('equal')
axarr[1][0].set_aspect('equal')
axarr[1][1].set_aspect('equal')

plt.suptitle('4-Component PCA')

我们添加到PCA技术中的每个附加维度捕获模型中的差异越来越少。 第一个组件是最重要的组件，其次是第二个组件，然后是第三个组件，依此类推。

我们还可以使用奇异值分解（SVD）将我们的原始数据集分解为其成分，从而减少维数。 要了解SVD背后的数学，请参阅本文。

SVD将原始变量分解为三个组成矩阵。 它主要用于从数据集中删除冗余功能。 它使用特征值和特征向量的概念来确定这三个矩阵。 由于本文的范围，我们不会进入它的数学，但让我们坚持我们的计划，即减少数据集中的维度。

让我们实现SVD并分解我们的原始变量：

from sklearn.decomposition import TruncatedSVD 
svd = TruncatedSVD(n_components=3, random_state=42).fit_transform(df[feat_cols].values)

让我们通过绘制前两个主要组成部分来可视化变换后的变量：

plt.figure(figsize=(12,8))
plt.title('SVD Components')
plt.scatter(svd[:,0], svd[:,1])
plt.scatter(svd[:,1], svd[:,2])
plt.scatter(svd[:,2],svd[:,0])

上面的散点图非常巧妙地向我们展示了分解的组件。 如前所述，这些组件之间没有太多相关性。

3.9 Independent Component Analysis

独立分量分析（ICA）基于信息理论，也是最广泛使用的降维技术之一。 PCA和ICA之间的主要区别在于PCA寻找不相关的因素，而ICA寻找独立因素。

如果两个变量不相关，则意味着它们之间没有线性关系。 如果它们是独立的，则意味着它们不依赖于其他变量。 例如，一个人的年龄与该人吃什么或他/她看多少电视无关。

**该算法假设给定变量是一些未知潜在变量的线性混合。 它还假设这些潜在变量是相互独立的，**即它们不依赖于其他变量，因此它们被称为观察数据的独立分量。

让我们直观地比较PCA和ICA，以便更好地了解它们的不同之处：

这里，图像（a）表示PCA结果，而图像（b）表示相同数据集上的ICA结果。

PCA的等式是x = W x。

这里，

• x是观察结果
• W是混合矩阵
• χ是源或独立组件

现在我们必须找到一个非混合矩阵，使组件尽可能独立。 测量组件独立性的最常用方法是非高斯性：

• 根据中心极限定理，独立分量之和的分布趋于正态分布（高斯分布）。
  

因此，我们可以寻找最大化独立分量的每个分量的峰度的变换。 Kurtosis是分布的第三阶段。 要了解有关峰度的更多信息，请访问here。
最大化峰度将使分布非高斯分布，因此我们将获得独立分量。

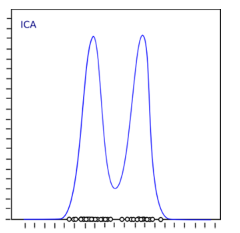
上述分布是非高斯分布，这又使组件独立。 让我们尝试在Python中实现ICA：

from sklearn.decomposition import FastICA 
ICA = FastICA(n_components=3, random_state=12) 
X=ICA.fit_transform(df[feat_cols].values)

这里，n_components将决定转换数据中的组件数。 我们使用ICA将数据转换为3个组件。 让我们想象一下它如何改变数据：

plt.figure(figsize=(12,8))
plt.title('ICA Components')
plt.scatter(X[:,0], X[:,1])
plt.scatter(X[:,1], X[:,2])
plt.scatter(X[:,2], X[:,0])

数据已被分成不同的独立组件，在上图中可以非常清楚地看到。 X轴和Y轴表示分解的独立分量的值。

现在我们将看一些使用投影技术减少数据维度的方法。

3.10 Methods Based on Projections

首先，我们需要了解投影是什么。 假设我们有两个向量，矢量a和矢量b，如下所示：

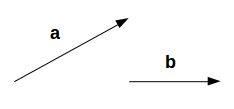
我们想要找到b的投影。 设a和b之间的角度为∅。 投影（a1）看起来像：

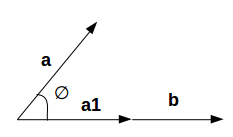
我们想要找到b的投影。 设a和b之间的角度为∅。 投影（a1）看起来像：

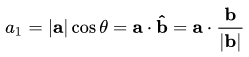
这里，

• a1 =投射到b上
• b = b方向的单位矢量

通过将一个矢量投影到另一个矢量上，可以减少维数。

在投影技术中，通过将其点投影到较低维空间来表示多维数据。现在我们将讨论不同的预测方法：

• 投射到有趣的方向：
  • 有趣的方向取决于具体问题，但一般来说，投影值是非高斯的方向被认为是有趣的
  • 与ICA（独立分量分析）类似，投影寻找最大化投影值的峰度的方向，作为非高斯性的度量
• 投影到流形上：

曾几何时，人们认为地球是平坦的。无论你去哪里，它都会保持平坦（让我们暂时忽视山脉）。但是，如果你继续向一个方向走，那么你最终会走向何方。如果地球平坦，那就不会发生。地球只看起来平坦，因为与地球的大小相比，我们是微不足道的。

地球看起来平坦的这些小部分是多方面的，如果我们将所有这些流形组合起来，我们就可以获得地球的大尺度视图，即原始数据。类似地，对于n维曲线，小扁平件是歧管，并且这些歧管的组合将给出我们原始的n维曲线。让我们看看投影到流形上的步骤：

• 我们首先寻找一个接近数据的流形
• 然后将数据投影到那个流形上
• 最后为了表示，我们展开了多方面
• 有各种技术可以实现多方面，所有这些技术都包含三个步骤：
  • 从每个数据点收集信息以构建具有数据点作为顶点的图
• 将上面生成的图转换为适合嵌入步骤的输入
• 计算（nXn）本征方程

让我们通过一个例子来理解流形投影技术。

如果歧管连续可微分到任何顺序，则称为平滑或可微分流形。 ISOMAP是一种旨在恢复非线性流形的完整低维表示的算法。它假设歧管是平滑的。

它还假设对于流形上的任何一对点，两点之间的测地距离（曲面上两点之间的最短距离）等于欧几里德距离（直线上两点之间的最短距离）。让我们首先想象一对点之间的测地线和欧几里德距离：

这里，

• Dn1n2 = X1和X2之间的测地距离
• dn1n2 = X1和X2之间的欧几里德距离

ISOMAP假设这两个距离相等。现在让我们看一下这种技术的更详细解释。如前所述，所有这些技术都采用三步法。我们将详细介绍这些步骤：

• 邻域图：
  • 第一步是计算所有数据点对之间的距离：
    dij =dχ（xi，xj）= || xi-xj || χ
    这里，
    d x（xi，xj）= xi和xj之间的测地距离
    || xi-xj || = xi和xj之间的欧几里德距离
  • 计算距离后，我们确定哪些数据点是流形的邻域
  • 最后生成邻域图：G = G（V，ℰ），其中顶点集合V = {x1，x2，…，xn}是输入数据点，边缘集合ℰ= {eij}表示邻域关系点之间
• 计算图形距离：
  • 现在我们通过图形距离计算流形中各点之间的测地距离
  • 图形距离是图G中所有点对之间的最短路径距离
• 嵌入：
  • 一旦我们得到距离，我们就形成了一个平方图距离的对称（nXn）矩阵
  • 现在我们选择嵌入向量来最小化测地距离和图形距离之间的差异
  • 最后，图形G通过（t Xn）矩阵嵌入到Y中

让我们用Python实现它，更清楚地了解我在说什么。我们将通过等距映射执行非线性降维。对于可视化，我们将只采用数据集的一个子集，因为在整个数据集上运行它将需要大量时间。

from sklearn import manifold 
trans_data = manifold.Isomap(n_neighbors=5, n_components=3, n_jobs=-1).fit_transform(df[feat_cols][:6000].values)

使用的参数：

• n_neighbors决定每个点的邻居数
• n_components决定流形的坐标数
• n_jobs = -1将使用所有可用的CPU核心

可视化转换的数据：

plt.figure(figsize=(12,8))
plt.title('Decomposition using ISOMAP')
plt.scatter(trans_data[:,0], trans_data[:,1])
plt.scatter(trans_data[:,1], trans_data[:,2])
plt.scatter(trans_data[:,2], trans_data[:,0])

您可以在上面看到这些组件之间的相关性非常低。 实际上，与我们之前使用SVD获得的组件相比，它们的相关性更低！

3.11 t- Distributed Stochastic Neighbor Embedding (t-SNE)

到目前为止，我们已经了解到PCA对于具有大量变量的数据集的降维和可视化是一个很好的选择。但是，如果我们可以使用更先进的东西呢？如果我们可以轻松地以非线性方式搜索模式，该怎么办？ t-SNE就是这样一种技术。我们可以使用两种方法来映射数据点：

• 局部方法：它们将流形上的附近点映射到低维表示中的附近点。
• 全局方法：他们试图在所有尺度上保留几何图形，即将流形上的附近点映射到低维表示中的附近点以及远处点到远点。
• t-SNE是能够同时保留数据的本地和全局结构的少数算法之一
• 它计算高维空间和低维空间中点的概率相似性
• 数据点之间的高维欧氏距离被转换为表示相似性的条件概率：
  

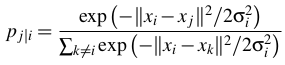
xi和xj是数据点，|| xi-xj || 表示这些数据点之间的欧几里德距离，σi是高维空间中数据点的方差

• 对于对应于高维数据点xi和xj的低维数据点yi和yj，可以使用以下方法计算类似的条件概率：

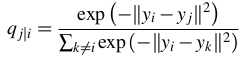
其中|| yi-yj || 表示yi和yj之间的欧几里德距离

• 在计算两个概率之后，它最小化了两个概率之间的差异

您可以参考这篇文章来更详细地了解t-SNE。

我们现在将在Python中实现它并可视化结果：

from sklearn.manifold import TSNE 
tsne = TSNE(n_components=3, n_iter=300).fit_transform(df[feat_cols][:6000].values)

n_components将决定转换数据中的组件数。 是时候可视化转换的数据：

plt.figure(figsize=(12,8))
plt.title('t-SNE components')
plt.scatter(tsne[:,0], tsne[:,1])
plt.scatter(tsne[:,1], tsne[:,2])
plt.scatter(tsne[:,2], tsne[:,0])

在这里，您可以清楚地看到使用强大的t-SNE技术转换的不同组件。

3.12 UMAP

t-SNE在大型数据集上运行良好，但它也有其局限性，例如大规模信息丢失，计算时间慢，无法有意义地表示非常大的数据集。统一流形近似和投影（UMAP）是一种降维技术，与t-SNE相比，可以保留尽可能多的本地数据结构，并且运行时间更短。听起来很有趣，对吧？

UMAP的一些主要优势是：

• 它可以毫不费力地处理大型数据集和高维数据
• 它结合了可视化的强大功能和减少数据维度的能力
• 除了保留本地结构外，它还保留了数据的全局结构。 UMAP将流形上的附近点映射到低维表示中的附近点，并对远点进行相同的处理

该方法使用k-最近邻的概念，并使用随机梯度下降来优化结果。它首先计算高维空间中的点之间的距离，将它们投影到低维空间，并计算该低维空间中的点之间的距离。然后，它使用随机梯度下降来最小化这些距离之间的差异。要更深入地了解UMAP的工作原理，请查看本文。

请参阅此处以查看UMAP的文档和安装指南。我们现在将在Python中实现它：

import umap
umap_data = umap.UMAP(n_neighbors=5, min_dist=0.3, n_components=3).fit_transform(df[feat_cols][:6000].values)

这里，

• n_neighbors确定使用的相邻点的数量
• min_dist控制允许嵌入的紧密程度。 值越大，嵌入点的分布越均匀

让我们想象一下转型：

plt.figure(figsize=(12,8))
plt.title('Decomposition using UMAP')
plt.scatter(umap_data[:,0], umap_data[:,1])
plt.scatter(umap_data[:,1], umap_data[:,2])
plt.scatter(umap_data[:,2], umap_data[:,0])

尺寸已经减小，我们可以想象不同的变换组件。 变换后的变量之间的相关性非常小。 让我们比较UMAP和t-SNE的结果：

我们可以看到，与从t-SNE获得的组件之间的相关性相比，从UMAP获得的组件之间的相关性非常小。 因此，UMAP倾向于提供更好的结果。

正如UMAP的GitHub存储库中所提到的，与t-SNE相比，它在保留数据全局结构方面的表现通常更好。 这意味着它通常可以提供更好的“全局”数据视图以及保留本地邻居关系。

深吸一口气。 我们已经涵盖了相当多的降维技术。 让我们简要总结一下可以使用它们的位置。

4. Brief Summary of when to use each Dimensionality Reduction Technique

在本节中，我们将简要总结我们所涵盖的每种降维技术的使用案例。 重要的是要了解在哪里，并且应该使用某种技术，因为它有助于节省时间，精力和计算能力。

缺失值比率：如果数据集中有太多缺失值，我们使用此方法来减少变量数量。我们可以删除其中包含大量缺失值的变量
低方差滤波器：我们应用此方法来识别和丢弃数据集中的常量变量。目标变量不会受到方差较小的变量的过度影响，因此可以安全地删除这些变量
高相关滤波器：具有高相关性的一对变量增加了数据集中的多重共线性。因此，我们可以使用此技术来查找高度相关的功能并相应地删除它们
随机森林：这是最常用的技术之一，它告诉我们数据集中存在的每个特征的重要性。我们可以找到每个特征的重要性并保持最顶层的特征，从而减少维数
后向特征消除和前向特征选择技术都需要大量的计算时间，因此通常用于较小的数据集
因子分析：这种技术最适合我们拥有高度相关的变量集的情况。它将变量基于它们的相关性划分为不同的组，并用因子表示每个组
主成分分析：这是处理线性数据最广泛使用的技术之一。它将数据划分为一组组件，试图解释尽可能多的方差
独立分量分析：我们可以使用ICA将数据转换为独立的组件，使用较少的组件来描述数据
ISOMAP：当数据非常非线性时，我们使用这种技术
t-SNE：当数据非常非线性时，这种技术也很有效。它对于可视化也非常有效
UMAP：此技术适用于高维数据。与t-SNE相比，其运行时间更短

End Notes

这是一篇关于减少维数的全面文章，你可以在任何地方找到它！ 我写了很多乐趣，并找到了一些处理我之前没有使用的大量变量的新方法（比如UMAP）。

处理数以千万计的功能是任何数据科学家必备的技能。 我们每天生成的数据量是前所未有的，我们需要找到不同的方法来确定如何使用它。 维度降低是一种非常有用的方法，在专业环境和机器学习黑客马拉松中为我创造了奇迹。

我期待在下面的评论部分听到您的反馈和想法。