1，线性表

顺序表

树存储结构

图 5 家庭族谱

图存储结构

　　　　图存储结构适合存储具有“多对多”关系的数据。

图 6 图存储结构示意图
 

　　如图 6 所示，从 V1 可以到达 V2、V3、V4，同样，从 V2、V3、V4 也可以到达 V1，这就是“多对多”的关系，满足这种关系的数据可以使用图存储结构。

算法时间复杂度和空间复杂度的计算

     算法，即解决问题的方法。同一个问题，使用不同的算法，虽然得到的结果相同，但是耗费的时间和资源是不同的。

比如：要拧一个螺母，使用扳手还是钳子是有区别的，虽然使用钳子也能拧螺母，但是没有扳手好用。
　　　　“条条大路通罗马”，解决问题的算法有多种，这就需要判断哪个算法“更好”。

算法VS程序

　　很多人误以为程序就是算法，其实不然：

• 算法是解决某个问题的想法、思路；
• 程序是在心中有算法的前提下编写出来的可以运行的代码。

　　例如，要解决依次输出一维数组中的数据元素的值的问题，首先想到的是使用循环结构（ for 或者 while ），在有这个算法的基础上，开始编写程序。
所以，算法相当于是程序的雏形。当解决问题时，首先心中要有解决问题的算法，围绕算法编写出程序代码。

有算法一定能解决问题吗？

　　对于一个问题，想出解决的算法，不一定就能解决这个问题。
　　例如： 

     　　拧螺 母，扳手相对于钳子来说更好使（选择算法的过程），但是在拧的过程（编写程序的过程）中发现螺母生锈拧不动，这时就需要另想办法。
   为了避免这种情况的发生，要充分全面地思考问题，尽可能地考虑到所有地可能情况，慎重选择算法（需要在实践中不断地积累经验）

“好”算法的标准

　　对于一个问题的算法来说，之所以称之为算法，首先它必须能够解决这个问题（称为准确性）。其次，通过这个算法编写的程序要求在任何情况下不能崩溃（称为健壮性）。
如果准确性和健壮性都满足，接下来，就要考虑最重要的一点：通过算法编写的程序，运行的效率怎么样。

运行效率体现在两方面：

• 算法的运行时间。（称为“时间复杂度”）
• 运行算法所需的内存空间大小。（称为“空间复杂度”）

  总结：

　　好算法的标准就是：在符合算法本身的要求的基础上，使用算法编写的程序运行的时间短，运行过程中占用的内存空间少，就可以称这个算法是“好算法”。

调查表明，人们对于软件或者 APP 的运行效率有极高的要求，

　　例如：对于网页打开的忍耐极限是 6 秒甚至更短，如果你设计的网页打开的时间超过 6 秒，多数人会在 4 秒甚至 3 秒的时候毫不犹豫地关掉而去浏览其他网页。在这个大背景下，一个好的“算法”更注重的是时间复杂度，而空间复杂度只要在一个合理的范围内就可以。

a) ++x; s=0;　　//a 代码的运行了 1 次
b) for (int i=1; i<=n; i++) { //b 代码的运行了 n 次 
     ++x;
     s+=x; 
}      
c) for (int i=1; i<=n; i++) { 
        for (int j=1; i<=n; j++) {//c 代码运行了 n*n 次。   
           ++x;
             s+=x;
 } }                     

时间复杂度的表示

算法的时间复杂度的表示方式为：(注意，是大写的字母O，不是数字0。)

         O(频度)  // 这种表示方式称为大“O”记法。

1. 去掉运行时间中的所有加法常数。（例如 n²+n+1，直接变为 n²+n）
2. 只保留最高项。（n²+n 变成 n²）
3. 如果最高项存在但是系数不是1，去掉系数。（n² 系数为 1）

常用的时间复杂度的排序

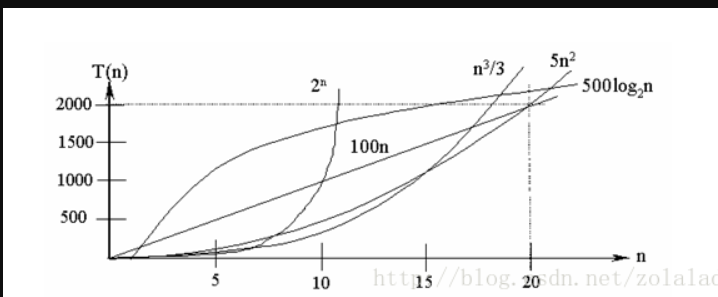
从图中可见，我们应该尽可能选用多项式阶O(n^k)的算法，而不希望用指数阶的算法。

      常见的算法时间复杂度由小到大依次为：Ο(1)＜Ο(log₂n)＜Ο(n)＜Ο(nlog₂n)＜Ο(n²)＜Ο(n³)＜…＜Ο(2ⁿ)＜Ο(n!)

       一般情况下，对一个问题（或一类算法）只需选择一种基本操作来讨论算法的时间复杂度即可，有时也需要同时考虑几种基本操作，甚至可以对不同的操作赋予不同的权值，以反映执行不同操作所需的相对时间，这种做法便于综合比较解决同一问题的两种完全不同的算法。

        ⑴ 找出算法中的基本语句；

　　　　算法中执行次数最多的那条语句就是基本语句，通常是最内层循环的循环体。

　　⑵ 计算基本语句的执行次数的数量级；

　　　　只需计算基本语句执行次数的数量级，这就意味着只要保证基本语句执行次数的函数中的最高次幂正确即可

　　　　注意：可以忽略所有  低次幂   和   最高次幂的系数。这样能够简化算法分析，并且使注意力集中在最重要的一点上：增长率。

　　⑶ 用大Ο记号表示算法的时间性能。

　　将基本语句执行次数的数量级放入大Ο记号中。

情况一：

 　　如果算法中包含嵌套的循环，则基本语句通常是最内层的循环体，如果算法中包含并列的循环，则将并列循环的时间复杂度相加。例如：

for (i=1; i<=n; i++)  
       x++;  
for (i=1; i<=n; i++)  
    　for (j=1; j<=n; j++)  
          x++;  

结果：第一个for循环的时间复杂度为Ο(n)，第二个for循环的时间复杂度为Ο(n²)，则整个算法的时间复杂度为Ο(n+n²)=Ο(n²)。

　　　　Ο(1)表示基本语句的执行次数是一个常数，一般来说，只要算法中不存在循环语句，其时间复杂度就是Ο(1)。其中Ο(log₂n)、Ο(n)、 Ο(nlog₂n)、Ο(n²)和Ο(n³)称为多项式时间，而Ο(2ⁿ)和Ο(n!)称为指数时间。

　　　　计算机科学家普遍认为前者（即多项式时间复杂度的算法）是有效算法，把这类问题称为P（Polynomial,多项式）类问题，而把后者（即指数时间复杂度的算法）称为NP（Non-Deterministic Polynomial, 非确定多项式）问题。

        一般来说多项式级的复杂度是可以接受的，很多问题都有多项式级的解——也就是说，这样的问题，对于一个规模是n的输入，在n^k的时间内得到结果，称为P问题。有些问题要复杂些，没有多项式时间的解，但是可以在多项式时间里验证某个猜测是不是正确。

　　比如问4294967297是不是质数？如果要直接入手的话，那么要把小于4294967297的平方根的所有素数都拿出来，看看能不能整除。还好欧拉告诉我们，这个数等于641和6700417的乘积，不是素数，很好验证的，顺便麻烦转告费马他的猜想不成立。大数分解、Hamilton回路之类的问题，都是可以多项式时间内验证一个“解”是否正确，这类问题叫做NP问题。

（4）在计算算法时间复杂度时有以下几个简单的程序分析法则:

　　(1).对于一些简单的输入输出语句或赋值语句,近似认为需要O(1)时间

　　(2).对于顺序结构,需要依次执行一系列语句所用的时间可采用大O下"求和法则"

　　对于复杂算法，可以认为将它分成几个容易估算的部分分别估算，然后利用求和法则和乘法法则计算整个算法的时间复杂度，

求和法则:是指若算法的2个部分时间复杂度分别为 T1(n)=O(f(n))和 T2(n)=O(g(n)),则 T1(n)+T2(n)=O(max(f(n), g(n))) （相同问题规模时）

           特别地,若T1(m)=O(f(m)), T2(n)=O(g(n)),则 T1(m)+T2(n)=O(f(m) + g(n))   （不相同问题规模时）

 　　(3).对于选择结构,如if语句,它的主要时间耗费是在执行then字句或else字句所用的时间,需注意的是检验条件也需要O(1)时间

　　(4).对于循环结构,循环语句的运行时间主要体现在多次迭代中执行循环体以及检验循环条件的时间耗费,一般可用大O下"乘法法则"

乘法法则: 是指若算法的2个部分时间复杂度分别为 T1(n)=O(f(n))和 T2(n)=O(g(n)),则 T1*T2=O(f(n)*g(n))   （不相同问题规模时和相同问题规模）

　　(5).对于复杂的算法,可以将它分成几个容易估算的部分,然后利用求和法则和乘法法则技术整个算法的时间复杂度

        另外还有以下2个运算法则:

    　　　　(1) 若g(n)=O(f(n)),则O(f(n))+ O(g(n))= O(f(n))；

　　　　　(2) O(Cf(n)) = O(f(n)),其中C是一个正常数

 （5）下面分别对几个常见的时间复杂度进行示例说明：

(1)、O(1)

         Temp=i;    i=j;     j=temp;                    

以上三条单个语句的频度均为1，该程序段的执行时间是一个与问题规模n无关的常数。算法的时间复杂度为常数阶，记作T(n)=O(1)。

注意：如果算法的执行时间不随着问题规模n的增加而增长，即使算法中有上千条语句，其执行时间也不过是一个较大的常数。此类算法的时间复杂度是O(1)。

(2)、O(n²)

2.1. 交换i和j的内容

sum=0；                 （一次）  
for(i=1;i<=n;i++)     （n+1次）执行n次后再回来判断不符合条件的(n+1)项，然后跳出循环继续执行  
   for(j=1;j<=n;j++) （n2次）  
    sum++；            （n2次）  

解：因为Θ(2n²+n+1)=n²（Θ即：去低阶项，去掉常数项，去掉高阶项的常参得到），所以T(n)= =O(n²)；

2.2. 

for (i=1;i<n;i++)  
 {   
     y=y+1;         ①     
     for (j=0;j<=(2*n);j++)      
        x++;         ②    

解： 语句1的频度是n-1
          语句2的频度是(n-1)*(2n+1)=2n²-n-1
          f(n)=2n²-n-1+(n-1)=2n²-2；

        又Θ(2n²-2)=n²
          该程序的时间复杂度T(n)=O(n²).  

　　一般情况下，对步进循环语句只需考虑循环体中语句的执行次数，忽略该语句中步长加1、终值判别、控制转移等成分，当有若干个循环语句时，算法的时间复杂度是由嵌套层数最多的循环语句中最内层语句的频度f(n)决定的。

(3)、O(n) 

a=0;  
  b=1;               ①  
  for (i=1;i<=n;i++) ②  
  {    
     s=a+b;　　　 ③  
     b=a;　　　　　④    
     a=s;　　　　　⑤  
  }  

解： 语句1的频度：2,        
           语句2的频度： n,        
          语句3的频度： n-1,        
          语句4的频度：n-1,    
          语句5的频度：n-1,                                  
          T(n)=2+n+3(n-1)=4n-1=O(n).
(4)、O(log₂n)   

不懂得可以看这个博主（与二分搜索树有关）：https://blog.csdn.net/li396864285/article/details/79820808

i=1;     ①  O(1)
hile (i<=n)  O(n) 
  i=i*2; ②  O(f(n))   则：2^f(n)<=n;f(n)<=log2n 

解： 语句1的频度是1,  
          设语句2的频度是f(n),   则：2^f(n)<=n;f(n)<=log₂n    
          取最大值f(n)=log₂n,
          T(n)=O(log₂n )

(5)、O(n³) 

for(i=0;i<n;i++)  
   {    
      for(j=0;j<i;j++)    
      {  
         for(k=0;k<j;k++)  
            x=x+2;    
      }  
   }  

解：当i=m, j=k的时候,内层循环的次数为k当i=m时, j 可以取 0,1,...,m-1 , 所以这里最内循环共进行了0+1+...+m-1=(m-1)m/2次所以,i从0取到n, 则循环共进行了: 0+(1-1)*1/2+...+(n-1)n/2=n(n+1)(n-1)/6所以时间复杂度为O(n³).

（5）常用的算法的时间复杂度和空间复杂度

一个经验规则：其中c是一个常量，如果一个算法的复杂度为c 、 log₂n 、n 、 n*log₂n ,那么这个算法时间效率比较高 ，如果是2ⁿ ,3ⁿ ,n!，那么稍微大一些的n就会令这个算法不能动了，居于中间的几个则差强人意。

           算法时间复杂度分析是一个很重要的问题，任何一个程序员都应该熟练掌握其概念和基本方法，而且要善于从数学层面上探寻其本质，才能准确理解其内涵。

拿时间换空间，用空间换时间

     算法的时间复杂度和空间复杂度是可以相互转化的。
比如：
     谷歌浏览器相比于其他的浏览器，运行速度要快。是因为它占用了更多的内存空间，以空间换取了时间。
　算法中，

     例如   判断某个年份是否为闰年时，

   （1）如果想以时间换取空间，算法思路就是：当给定一个年份时，判断该年份是否能被4或者400整除，如果可以，就是闰年。

   （2）如果想以空间换时间的话，判断闰年的思路就是：把所有的年份先判断出来，存储在数组中（年份和数组下标对应），如果是闰年，数组值是1，否则是0；当需要判断某年是否为闰年时，直接看对应的数组值是1还是0，不用计算就可以马上知道。

       例如    当一个算法的空间复杂度为一个常量，即不随被处理数据量n的大小而改变时，可表示为O(1)；

　　　　　当一个算法的空间复杂度与以2为底的n的对数成正比时，可表示为0(10g2n)；

　　　　　当一个算法的空I司复杂度与n成线性比例关系时，可表示为0(n).

　　　若形参为数组，则只需要为它分配一个存储由实参传送来的一个地址指针的空间，即一个机器字长空间；若形参为引用方式，则也只需要为其分配存储一个地址的空间，用它来存储对应实参变量的地址，以便由系统自动引用实参变量。

   x=1; 

for(i=1;i<=n;i++) 

        for(j=1;j<=i;j++)

           for(k=1;k<=j;k++)

               x++; 　　

  i=n-1;            

while(i>=0&&(A[i]!=k))       

      i--;        

return i;       

 

数据的逻辑结构和物理结构

   （1）数据元素之间的相互联系方式称为数据的逻辑结构 。数据的逻辑结构是对数据元素之间逻辑关系的描述，它可以用一个数据元素的集合和定义在此集合上的若干关系来表示。数据的逻辑结构经常被简称为数据结构。

按照数据的逻辑结构来分，有两种形式：线性结构和非线性结构。线性结构是指 除第一个和最后一个数据元素外，每个数据元素有且只有一个前驱元素和一个后继元素，而非线性数据结构则会有零个或多个前驱元素和零个或多个后继元素。

   （2）数据元素在计算机中的存储表示方式称为数据的存储结构 ，也称物理结构。任何需要计算机进行管理和处理的数据元素都必须首先按某种方式存储在计算机中，数据存储结构能正确地表示出数据元素间的逻辑关系。

          按照数据的存储结构来分，有两种类型：顺序存储结构和链式存储结构。

　　　顺序存储结构是把数据元素存储在一块连续地址空间的内存中，其特点是逻辑上相邻的数据元素在物理上（即内存存储位置上）也相邻，数据间的逻辑关系表现在数据元素的存储位置关系上。

　　　链式存储结构的关键是使用节点，节点是由数据元素域与指针域组合的一个整体，指针将相互关联的节点衔接起来。其特点是逻辑上相邻的元素在物理上不一定相邻，数据间的逻辑关系表现在节点的衔接关系上。

          数据的逻辑结构是从逻辑关系角度观察数据，它与数据的存储无关，是独立于计算机的。而数据的存储结构是逻辑结构在计算机内存中的实现，它是计算机处理的逻辑。

数据结构与算法的联系：  

        程序=算法+数据结构。数据结构是算法实现的基础，算法总是要依赖于某种数据结构来实现的。往往是在发展一种算法的时候，构建了适合于这种算法的数据结构。  算法的操作对象是数据结构。算法的设计和选择要同时结合数据结构，简单地说数据结构的设计就是选择存储方式，如确定问题中的信息是用数组存储还是用普通的变量存储或其他更加复杂的数据结构。算法设计的实质就是对实际问题要处理的数据选择一种恰当的存储结构，并在选定的存储结构上设计一个好的算法。不同的数据结构的设计将导致差异很大的算法。数据结构是算法设计的基础。用一个形象的比喻来解释：开采煤矿过程中，煤矿以各种形式深埋于地下。矿体的结构就像相当于计算机领域的数据结构，而煤就相当于一个个数据元素。开采煤矿然后运输、加工这些“操作”技术就相当于算法。显然，如何开采，如何运输必须考虑到煤矿的存储（物理）结构，只拥有开采技术而没有煤矿是没有任何意义的。算法设计必须考虑到数据结构，算法设计是不可能独立于数据结构的。 另外，数据结构的设计和选择需要为算法服务。如果某种数据结构不利于算法实现它将没有太大的实际意义。知道某种数据结构的典型操作才能设计出好的算法。  
总之，算法的设计同时伴有数据结构的设计，两者都是为最终解决问题服务的。 

数据结构与算法的区别：

  数据结构关注的是数据的逻辑结构、存储结构以及基本操作，而算法更多的是关注如何在数据结构的基础上解决实际问题。算法是编程思想，数据结构则是这些思想的逻辑基础。