大模拟！！！

说实话，我认为本题的算法并不是搜索，而是模拟，题目已经很明确的说了，\(n\)一共有\(7\)种情况，我们把这七种情况一个一个分情况讨论，答案就出来了。

\[\text{正式进入题目(咳咳，严肃）}\]
由于题目要求将每一次所变换的图形与原图形进行比较，所以定义数组\(a[15][15],b[15][15],c[15][15],d[15][15](\text{题目申明}1 \leq n\leq10)\),\(a\)数组表示第一个输入的矩阵，\(b\)数组表示变换后的矩阵，\(c\)数组表示要对照的矩阵，\(d\)数组为将要存放的矩阵，所以可以写出以下判断\(b\)矩阵与\(c\)矩阵相同的代码
↓↓↓

for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
     if(b[i][j]!=c[i][j])
     return 0;
     return 1;

简单明了，蒟蒻都能懂！

\[First:n=1\]
设原矩阵为↓↓↓

11 12 13
21 22 23
31 32 33

那么，经过顺时针转\(90\)度的矩阵为

31 21 11
32 22 12
33 23 13

列出\(i\)(行)与\(j\)(列)的关系，如下：

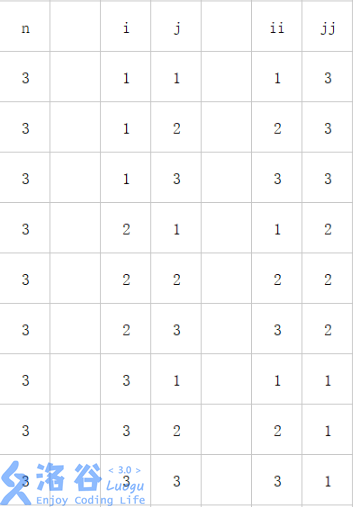
再进行找规律，经推敲可得
\[b[j][n-i+1]=a[i][j]\]
再与前面所说的判断合在一起，可得：

bool work1()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        b[j][n-i+1]=a[i][j];
    }
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
     if(b[i][j]!=c[i][j])
     return 0;
     return 1;
}

\(∴\)当\(n=1\)时，代码打好了。

\[Second:n=2\]
相同的，设原矩阵为↓↓↓

11 12 13
21 22 23
31 32 33

那么，经过顺时针转\(180\)度的矩阵为

33 32 31
23 22 21
13 12 11

列出\(i\)(行)与\(j\)(列)的关系，如下：

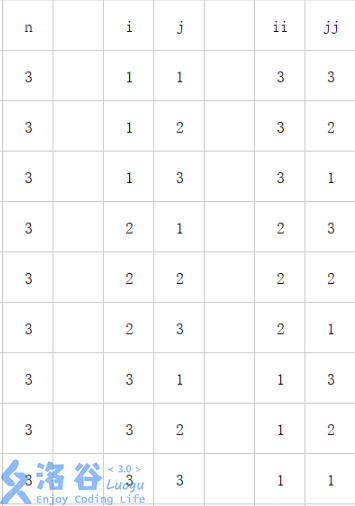
分析可得
\[b[n-i+1][n-j+1]=a[i][j]\]
代码实现：

bool work2()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        b[n-i+1][n-j+1]=a[i][j];
    }
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
     if(b[i][j]!=c[i][j])
     return 0;
     return 1;
}

当然，当\(n=2\)时，也可以看做进行了两次\(1\)操作，即：

void work2()
{
    work1(); //第一次操作
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
      a[i][j]=b[i][j];  //重置矩阵
      work1();  //第二次操作
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
     if(b[i][j]!=c[i][j])
     return 0;
     return 1;
}

两代码的结果相同，但前者效率较高，后者代码短小精悍，更好理解。

\(∴\)当\(n=2\)时，代码打好了。
\[QAQ\]

\[Third:n=3\]
同样的，设原矩阵为↓↓↓

11 12 13
21 22 23
31 32 33

那么，经过顺时针转\(270\)度的矩阵为

13 23 33
12 22 32
11 21 31

列表：

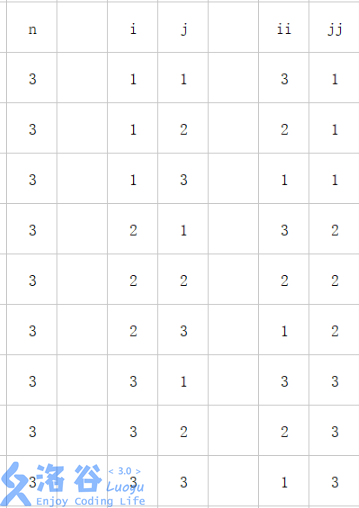
这次规律有一些难找了，是
\[b[n-j+1][i]=a[i][j]\]
于是

bool work3()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        b[n-j+1][i]=a[i][j];
    }
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
     if(b[i][j]!=c[i][j])
     return 0;
     return 1;
}

也可以看作先进行一次\(1\)操作再进行一次\(2\)操作
代码：

bool work3()
{
    work1();  //第一次操作
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
      a[i][j]=b[i][j];   //重置矩阵
      work2();   //第二次操作
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
     if(b[i][j]!=c[i][j])
     return 0;
     return 1;
}

\[n=3\text{完工！}\]

\[Fourth:n=4\]
同样的，设原矩阵为↓↓↓

11 12 13
21 22 23
31 32 33

那么，经过反射的矩阵为

13 12 11
23 22 21
33 32 31

又是无聊的列表：

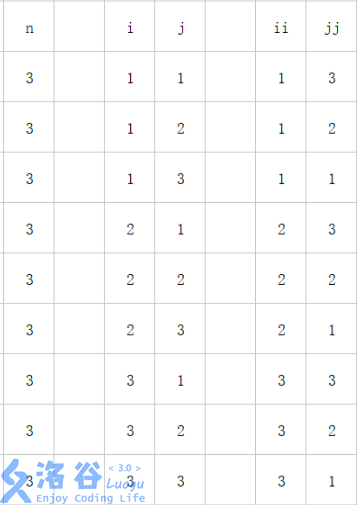
可以找出
\[b[i][n-j+1]=a[i][j]\]
代码实现：

bool work4()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        b[i][n-j+1]=a[i][j];  
    }
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
     if(b[i][j]!=c[i][j])
     return 0;
     return 1;
}

\[OK\]

\[Fifth:n=5\]
\(5\)操作就是将\(4,1,2,3\)操作混和(粗略的说法),作者为了偷懒，\(QAQ\),就不找规律了，给出代码：

bool work5()
{
    work4();
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
      a[i][j]=d[i][j];    //重置矩阵  
      if(work1())
      return 1;
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
      a[i][j]=d[i][j];   //重置矩阵 
      if(work2())
      return 1;
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
      a[i][j]=d[i][j];   //重置矩阵 
      if(work3())
      return 1;
      return 0;
}

\[\text{逃}\]

\[Sixth:n=6\]
没有操作，直接比较：

bool work6()
{
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
     if(b[i][j]!=c[i][j])
     return 0;
     return 1;
}

\[easy\]

\[Seventh:n=7\]
直接输出\(7\)即可

   cout<<7;

核心代码已经打完了，我们可以将代码美观化，用一个\(work\)函数把它们包起来

void work()
{
    if(work1())
    {
        cout<<1;
        return ;
    }
    if(work2())
    {
        cout<<2;
        return ;
    }
    if(work3())
    {
        cout<<3;
        return ;
    }
    if(work4())
    {
        cout<<4;
        return ;
    }
    if(work5())
    {
        cout<<5;
        return ;
    }
    if(work6())
    {
        cout<<6;
        return ;
    }
    cout<<7;
}

\(My complete code\)

#include<bits/stdc++.h>
using namespace std;
int n;
char a[15][15],b[15][15],c[15][15],d[15][15];
bool work1()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        b[j][n-i+1]=a[i][j];
    }
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
     if(b[i][j]!=c[i][j])
     return 0;
     return 1;
}
bool work2()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        b[n-i+1][n-j+1]=a[i][j];
    }
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
     if(b[i][j]!=c[i][j])
     return 0;
     return 1;
}
bool work3()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        b[n-j+1][i]=a[i][j];
    }
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
     if(b[i][j]!=c[i][j])
     return 0;
     return 1;
}
bool work4()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        b[i][n-j+1]=a[i][j];
    }
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
     if(b[i][j]!=c[i][j])
     return 0;
     return 1;
}
bool work5()
{
    work4();
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
      a[i][j]=b[i][j];  
      if(work1())
      return 1;
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
      a[i][j]=b[i][j]; 
      if(work2())
      return 1;
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
      a[i][j]=b[i][j]; 
      if(work3())
      return 1;
      return 0;
}
bool work6()
{
    for(int i=1;i<=n;i++)
      for(int j=1;j<=n;j++)
     if(b[i][j]!=c[i][j])
     return 0;
     return 1;
}
void work()
{
    if(work1())
    {
        cout<<1;
        return ;
    }
    if(work2())
    {
        cout<<2;
        return ;
    }
    if(work3())
    {
        cout<<3;
        return ;
    }
    if(work4())
    {
        cout<<4;
        return ;
    }
    if(work5())
    {
        cout<<5;
        return ;
    }
    if(work6())
    {
        cout<<6;
        return ;
    }
    cout<<7;
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
     {
        cin>>a[i][j];
        d[i][j]=a[i][j];
     }
      
    for(int i=1;i<=n;i++)
     for(int j=1;j<=n;j++)
      cin>>c[i][j];
    work();
    return 0; //完美的结束QAQ
}