---恢复内容开始---
- 这只是一篇草稿,还没排版,之前一直想给自己写一个文章的模板,一直还没写,所以估计写的比较慢,所以先放出来文章,后面再来填坑吧。 这篇文章的初衷是看到面试问题有问到红黑树,甚至有手撕红黑树代码的?可怕,红黑树的讨论情况很多,一不小心就绕进去,真让人犯难,而且网上的文章各有各的说法,不少人理解甚至是错误的。
- 红黑树:红黑树是一种二叉平衡树,二叉查找树,它牛逼之处就在于它足够的平衡,可以达到高度至多2lg(n+1),所以在java中的treemap和c++ set, multiset, map, multimap就使用的红黑树。
- 红黑树的性质:1. 结点分为红色和黑色两种 2.根节点是黑色的 3.每个叶子结点(nil)是黑色的(就是空代表了黑色) 4.不存在父子都是红色的情况(连续两个红色) 5.任意孩子到根节点的路径上的黑色数量都是相等的(important)
- 本文将解释 以下内容:
1. 红黑树的插入(简单的插入)与调整(调整平衡)。
2. 红黑树的删除(也带有调整,使其便于调整平衡)与调整(调整平衡)。
### 插入
#### 插入方式:
先考虑插入什么颜色的结点,这里需要说明颜色只是我们用于保证平衡的一种方法,与数据无关。 因为插入黑色结点除非在根节点,否则一定会导致一个分支上的所有子分支都多了一个黑,如此不满足性质5(简称 路黑同)。所以我们插入红色。插入方式就是普通的二叉排序树的插入方式。就这么简单。
#### 调整:
因为插入的调整相对简单,我们可以将所有的情况列举出来然后讨论,列举的依据是:因为插入红色的结点不会对插入节点的子节点造成任何影响(即符合性质1-5,当我在做任何断言时,最好自己试试),所以仅需考虑插入结点的祖先的情况。
(图实在太多了,所以暂时手画了sorry)

具体而言我们要做的就是讨论一段区间,它的所有情况必须满足调整后对祖先和子孙都而言都仍然平衡,因为原来的两段都是平衡的,所以只需保证在讨论区间中是的任意左右子树满足性质,并且不改变原来和祖先和子树的接口,那么就一定能维持性质不变。
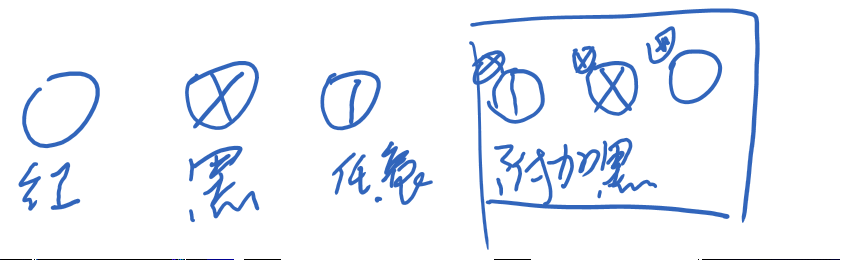
图中从左到右,分别是红色,黑色,任意颜色,附加黑(意思是除了原本结点带有的颜色还附加一层黑色,用处后面用到的时候再讲),
图中没有画出儿子结点不代表它儿子就是nil,如果有叶子结点会标nil的。
下图为所有情况
情况1:单个结点,没有父节点。
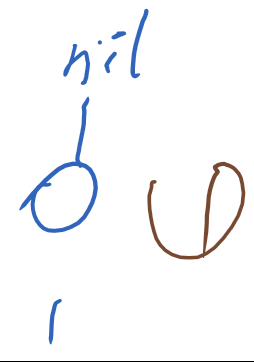
调整方法:红色变成黑色,性质2(简称 根黑),
情况2: 父节点是黑色,这样本来就是平衡的,但是由于讨论的结点儿子可能是红色,可以将这种情况转化成讨论它的儿子的情况,它的儿子的父节点是红色,对应接下来正好要讨论的情况3,所以情况2应该算情况3的一种子情况。
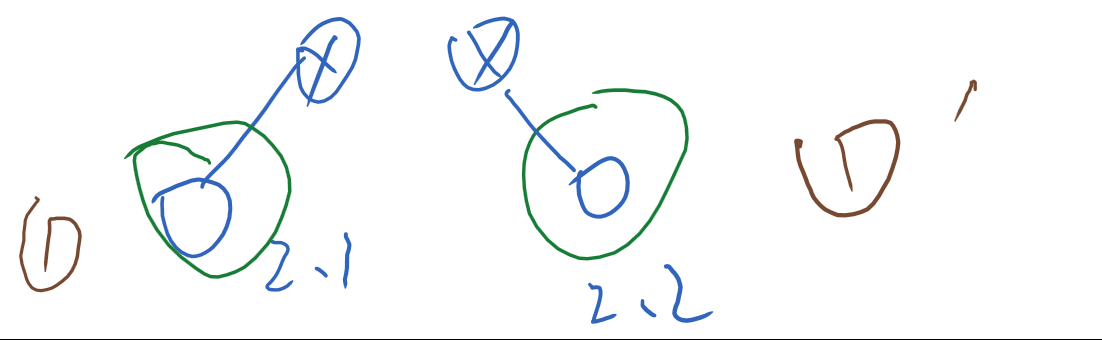
情况3:父节点是红色
分为两种情况, 一个是父的右孩子,一个是父的左孩子。
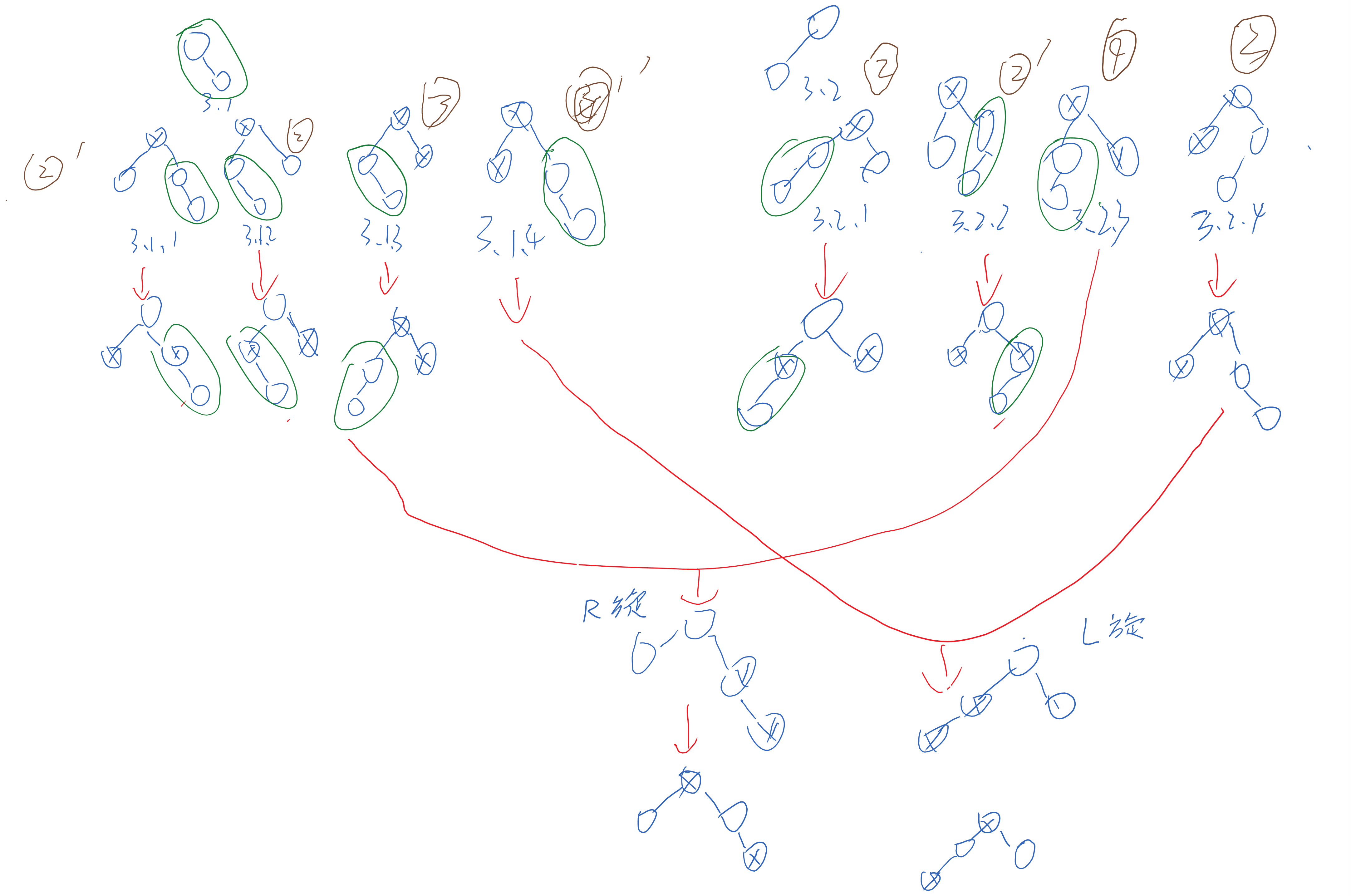
对于情况3.1.1, 只需将父节点和叔父结点变成黑色,然后祖父结点变成红色,就可以维持两个分支的黑色结点一致,并且没有两个红色,可以对照满足了所有性质,这就算是恢复好了,但仅仅是针对图中最上方的结点的子树,若以调整后最上方的红色结点作为讨论对象,讨论他的父结点情况,就又可以递归的分类讨论进行恢复,实际就是算法中的递归调用。
对于情况3.1.2 方式类似3.1.1
对于情况3.1.3, 可以先以红-红中的父节点进行左旋转,然后和情况3.2.3一样了,只需再以它为中心右旋一次,并如图变换颜色即可,最重要的依据就是分支的黑色要一致。所以调整后整棵树就恢复好了。因为讨论区间分别和子树以及子树连接的部分的红色维持不变,所以不会影响到原本的祖先和子孙的平衡情况。
对于其他情况,可以类似上面的四种情况进行操作,不再一一介绍,为了和教科书上(算法导论)保持一致,并且简化情况,我们需要将多种情况进行合并。合并的最后结果只剩下三种情况。如图中棕色的标号, (要记就记以下的结果)
①代表了第一种情况,这里把只有一个红色结点的情况归类为了父节点为黑色,实际上也是这么定义的,根节点的父节点为nil,nil为黑色,这样就进行了统一。
①归纳了情况:插入节点的父和叔节点是红色时,把他们变黑,再把爷爷变红,递归调用爷爷作为参数继续算法,
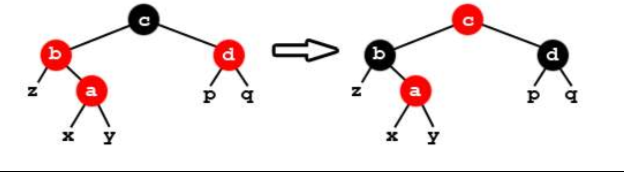
②归纳了情况:插入节点的父是红色uncle是黑色时,如果自己是父的右结点,先左旋到情况③
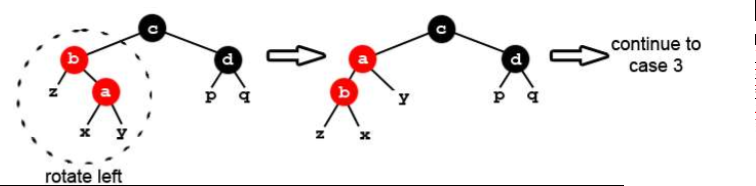
③归纳了情况:自己是父的左结点)然后再把fa和uncle变成黑色,grandparent变成红色再以父亲为参数右旋
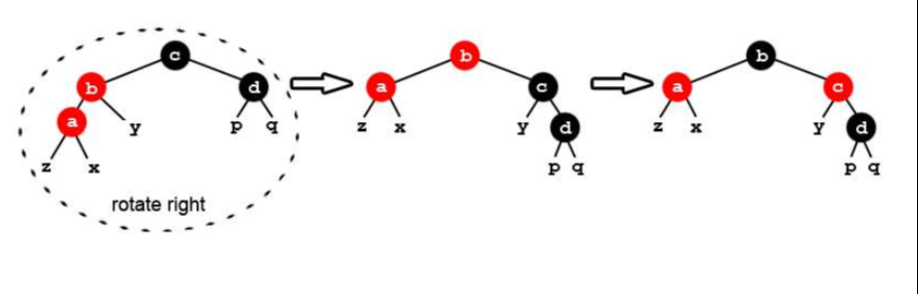
对应的还有①', ②',③',它和①, ②,③的区别就在于讨论的结点是在左子树还是右子树,操作方法是对称的,所以恢复算法一共有六种情况,但是三种也对。
附上代码:

#插入方法 RB-INSERT(T,z): #z就是插入的结点也是fix时当前讨论的结点 y = T.nil x = T.root while x != T.nil y = x if z.key < x.key x = x.left else x = x.right z.p = y if y == T.nil T.root = z else if z.key < y.key y.left = z else y.right = z z.left = T.nil z.right = T.nil z.color = RED RB-INSERT-FIXUP(T,z)
 View Code
View Code
---
### 删除:
删除情况讨论如果按照之前的将所有情况都讨论出来,那会很累,并且会绕进去, 所以我们还是根据现有的算法,来讨论分类
##### 删除的方式:根据情况删除时就做一些调整。
##### 主要的讨论分类方式:将删除分类为1.如果删除的结点只有一个孩子(不考虑nil),又可继续讨论下去,那个孩子是左孩子还是右孩子,
2.如果删除的结点有两个孩子,同样也可详细讨论 ,当然你也可以说还有一种情况,如果删除的结点一个孩子都没有,那种情况只用单纯的删除,删除过程中没有进行额外的操作,所有删除操作都要进行删除步骤,所以这里不进行讨论,注意到我们仅讨论了删除节点为根的子树情况,而没有讨论它的祖先结点,不是因为不影响,而是在删除过程中仅需要对以上几种情况分开讨论以进行额外的操作,便于删除恢复。
##### 删除的具体情况: 删除过程我们的主要目的是保证通过一些方法让整棵树仍然保持平衡(加附加黑的方式),然后在恢复的过程中解决附加黑的问题,以下讨论中a为待删除结点
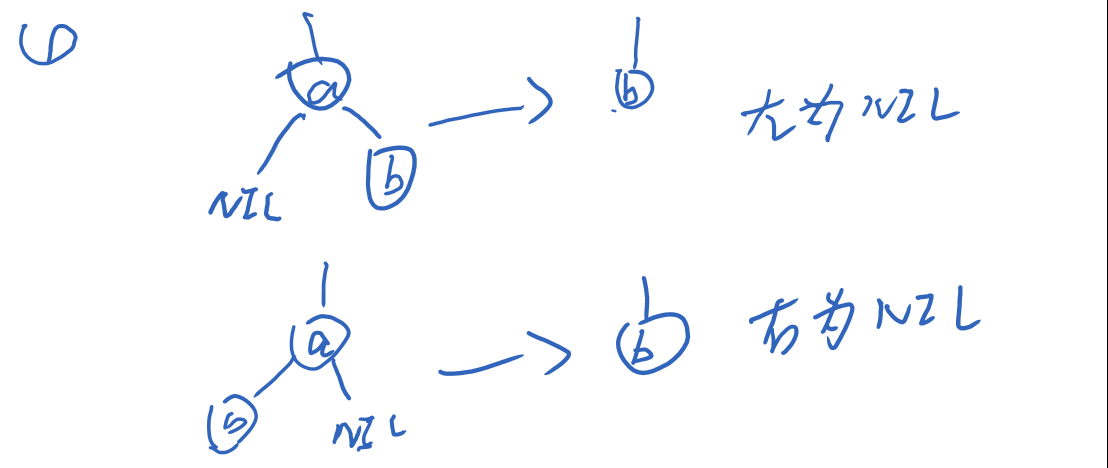
删除掉a,将另一个结点作为替换,因为 原来的a结点可能就是黑色的,这样a的子树就少了一个黑色,所以将b涂成黑色。我们发现这种情况就不再需要调整了。已经满足了要求的各种性质,不信可以试试。
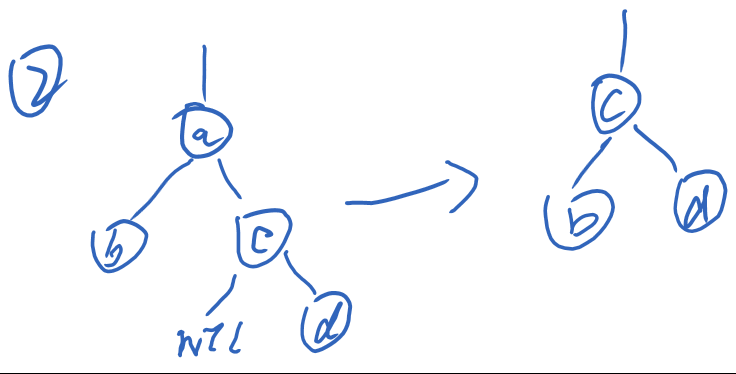
如果有两个孩子的话,并且 a(待删除结点)的儿子结点的左儿子为nil,就说明a是c最小的后继,删除a后,将c移动到a的位置,当然也可以用a的左子树中最大的数即a的前驱来替换他。除此之外,这种情况下,c必须和a的颜色相同,目的是使得改动最小,但是当a是黑色的时候,由于c,d根据性质必有一黑,当c是黑时,c替换后,c的分支相对于原来,少了一个黑色的结点,这时候就需要多加一重黑色来保证平衡
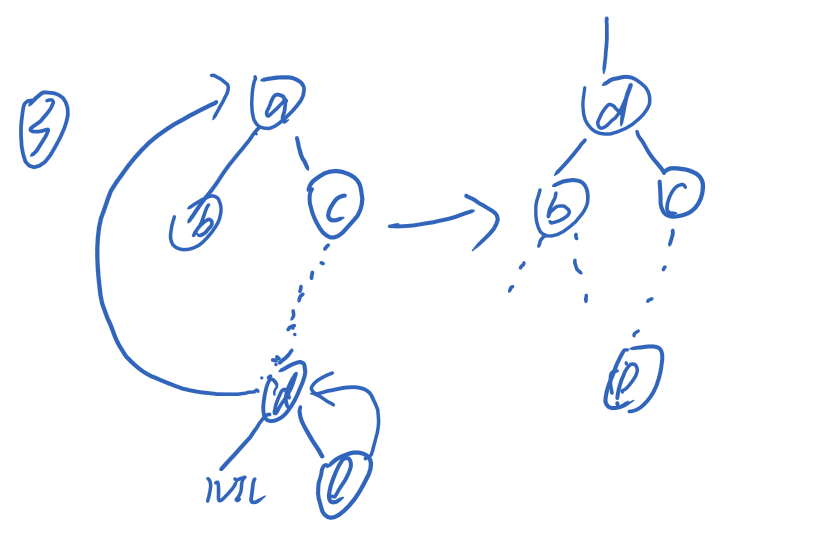
如果有两个孩子,并且a的儿子结点的儿子结点不为空,那么,通过找到左儿子的最小值,即dfs一直找最左儿子为nil的d,将它和a进行交换,然后e代替nil,同理还是d代替a的颜色,这时a为黑,且d为黑时就会不平衡,这时候如同情况2也需要给e多加一层黑色。
算法中①的情况因为左为nil和右为nil操作虽然对称,但是不一样,所以一般分成四种情况
##### 删除恢复,
最激动人心的时刻,删除恢复,不知是谁想的附加黑色这种骚操作,经过了上面的删除,我们现在只需要考虑恢复的情况只有如何将附加黑情况进行处理,基本思路是只考虑附加黑结点的子树以外的结点,因为算法试图将附加黑不断向树根传递,来达到在某一部消除的方式来恢复。
具体的讨论情况分为 附加黑结点的兄弟是1.红,2.黑(有分为三种情况: 1。兄弟的儿子为全黑 2.左红右黑 3.左any右红 )自己画画是否讨论完全了。 这样算一共4种子情况如下:
情况1:
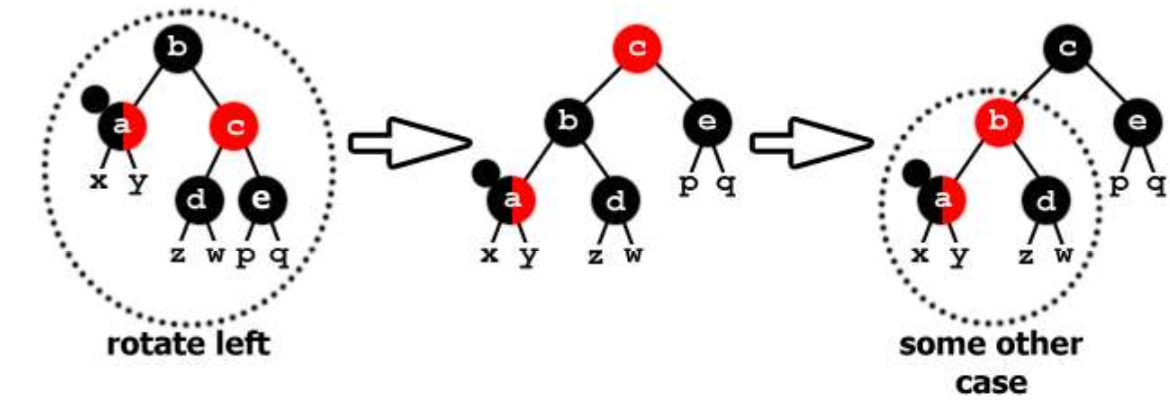
这种情况是 附加黑的兄弟是红色,进行左旋,对应了第二大类的讨论。
情况2:
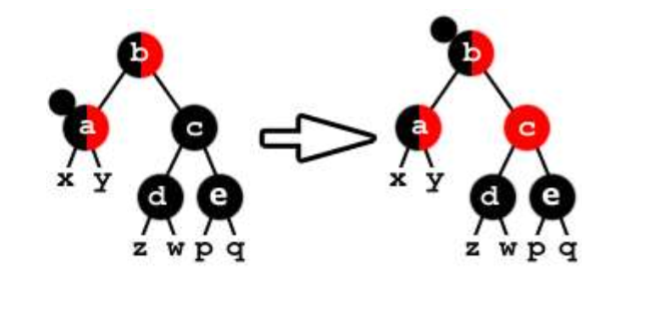
兄弟为黑,并且兄弟儿子全黑,这时候将附加黑向上传递,这样右边就多了一重黑色,所以将c改成红色,b的子树就满足要求了,然后继续以b为结点进行递归
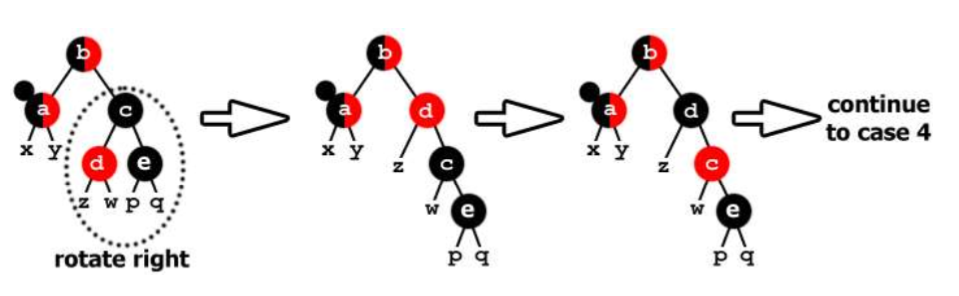
兄弟为黑并且左红右黑,通过以c为中心右旋再交换dc颜色就达到了情况4
情况4:
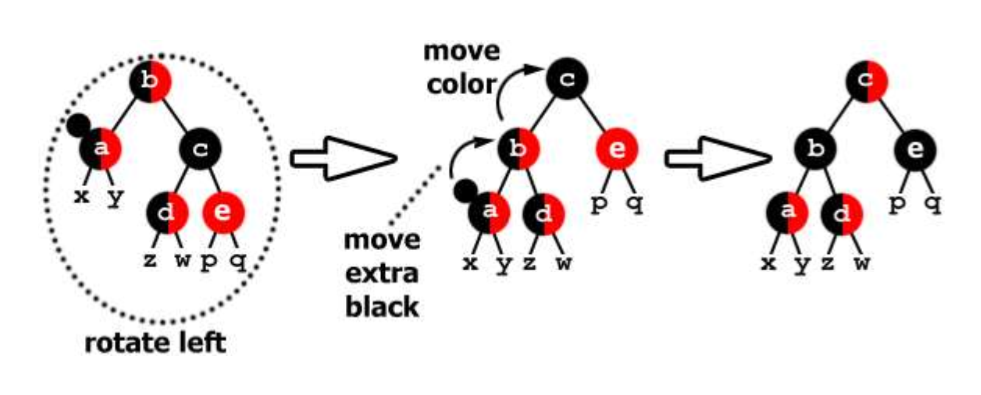
通过以b为中心左旋,这时我们发现左边和右边确定的黑分别为2和1,原来是1和1,所以需要给右边增加一层黑,通过将附加黑给b让b称为黑色,同时使得e为黑色,这样就满足了左2黑右2黑,但是要保持原来的黑色数为1,所以就将c改成原来b位置应有的任意
- 以上四种情况只考虑了a(带附加黑的点)是左儿子的情况, 同样右儿子是对称,所以和插入一样,4种基本情况实际是2x4种详细情况
以下为删除的伪代码:

RB-DELETE(T,z): y = z y-origin-color = y.color if z.left == T.nil x = z.right RB-TRANSPLANT(T, z, z.right) else if z.right ==T.nil x = z.left RB-TRANSPLANT(T,z,z.left) else y = TREE-MINIMUN(z,right) y-original-color = y.color x = y.right if y.p == z x.p = y else RB-TRANPLANT(T,y,y.right) y.right = z.right y.right.p = y RB-TRANSPLANT(T,z,y) y.left = z.left y.left.p = y y.color = z.color if y-original-color ==BLACK RB-DELETE-FIXUP(T,x)

RB-DELETE-FIXUP(T,x) while x!=T.root and x.color ==BLACK: if x== x.p.left w = x.p.right if w.color ==RED # case 1 w.color = BLACK x.p.color = RED LEFT-ROTATE(T,x.p) w = x.p.right if w.left.color ==BLACK and w.right.color ==BLACK w.color = RED #case 2 x = x.p else if w.right.color ==BLACK w.left.color = BLACK #case 3 w.color = RED RIGHT-ROTATE(T,w) w = x.p.right w.color = x.p.color #case 4 x.p.color = BLACK w.right.color = BLACK LEFT-ROTATE(T, x.p) x = T.root else (same as then clause with "right" and left exchanged ) #symetric case x.color = BLACK
