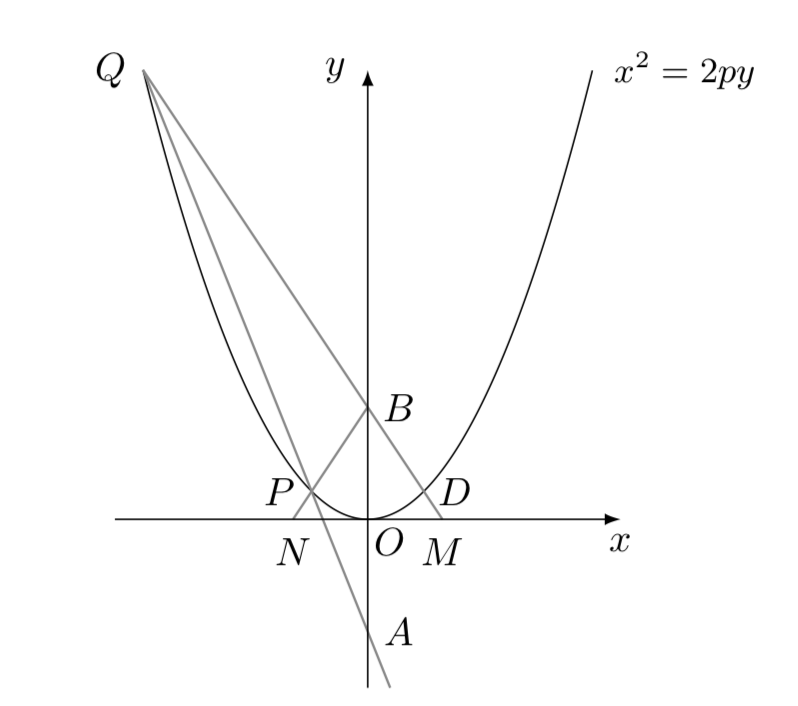
如图,已知抛物线的方程为\(x^2=2py,p>0\),过点\(A\left(0,-1\right)\)作直线\(l\)与抛物线相交于\(P,Q\)两点,点\(B\)的坐标为\((0,1)\),连结\(BP,BQ\),且\(QB\),\(BP\)与\(x\)轴分别相交于点\(M,N\),\(QB\)与抛物线交于另一点\(E\),如果\(QB\)的斜率与\(PB\)的斜率之积为\(-3\),那么\(\angle MBN\)的大小为\((\qquad)\)
\(\mathrm{A}.\dfrac{\pi}{2}\) \(\qquad\mathrm{B}.\dfrac{\pi}{4}\) \(\qquad\mathrm{C}.\dfrac{2\pi}{3}\) \(\qquad\mathrm{D}.\dfrac{\pi}{3}\)
解析:
由抛物线的几何平均性质我们有 \[y_Q\cdot y_P=y_A^2=y_B^2=y_Q\cdot y_D.\]因此 \(y_P=y_D\),所以 \(P,D\)两点关于 \(y\)轴对称,又因为 \(k_{QB}\cdot k_{PB}=-3\),所以 \(k_{PB}=\sqrt{3}\),于是 \[\angle MBN=\dfrac{\pi}{3}.\]