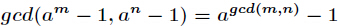重要性质：

$gcd(a,b)=gcd(b,a)$（交换律）

$gcd(-a,b)=gcd(a,b)$

$gcd(a,a)=|a|$

$gcd(a,0)=|a|$

$gcd(a,1)=1$

$gcd(a,b)=gcd(b, a \ mod \ b)$

$gcd(a,b)=gcd(b, a-b)$

如果有附加的一个自然数m,

则: $gcd(ma,mb)=m * gcd(a,b)$ (分配律)

$gcd(a+mb ,b)=gcd(a,b)$

如果m是a和b的最大公约数，

则： $gcd(a/m ,b/m)=gcd(a,b)/m$

在乘法函数中有：

$gcd(ab,m)=gcd(a,m) * gcd(b,m)$

两个整数的最大公约数主要有两种寻找方法：

• 两数各分解质因数，然后取出同样有的质因数乘起来

*辗转相除法（扩展版）

和最小公倍数（lcm）的关系：

$gcd(a, b) * lcm(a, b) = ab$

a与b有最大公约数，

两个整数的最大公因子可用于计算两数的最小公倍数，或分数化简成最简分数。

两个整数的最大公因子和最小公倍数中存在分配律：

* $gcd(a, lcm(b, c)) = lcm(gcd(a, b), gcd(a, c))$

* $lcm(a, gcd(b, c)) = gcd(lcm(a, b), lcm(a, c))$

$在坐标里，将点(0, 0)和(a, b)连起来，通过整数坐标的点的数目（除了(0, 0)一点之外）就是gcd(a, b)。$

以上转自 百度百科。

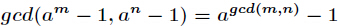
更一般的推论: $gcd(A, B) = 1$ $=>$
$\ \ \ \ \ \ \ \ \ \gcd（A^m - B^m，A^n - B^n）= A^{gcd(m，n)} - B^{gcd(m，n)}$

• 若 $a∗c≡b∗c (mod \ p),gcd(c,p)=d,则a≡b (mod \dfrac{p}{d})$