题意：
$给你n,k，M = 2008^{n}\%k，求2008^{M}\%k$
思路：
唯一分解定理分解质因数。
利用约数之和是积性函数的性质。对每个质因子的幂求约数之和。每个素因子的幂的约数之和是一个等比数列。用等比数列求和公式求的时候有一个坑点是除法取模时可能不存在逆元，所以只能通过别的方法来做。
比如可以套一个公式或者利用分治法求等比数列的和。
1、除法取模转化公式。

$AC \ Code:$

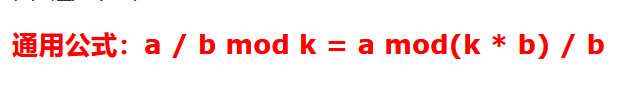
#include<iostream>
#include<cstring>
#include<queue>
#include<map>
#include<cmath>
#include<set>
#include<stack>
#include<cstdio>
#include<sstream>
#include<vector>
#include<bitset>
#include<algorithm>

using namespace std;
#define read(x) scanf("%d",&x)
#define Read(x,y) scanf("%d%d",&x,&y)
#define gc(x)  scanf(" %c",&x);
#define mmt(x,y)  memset(x,y,sizeof x)
#define write(x) printf("%d\n",x)
#define pii pair<int,int>
#define INF 0x3f3f3f3f
#define ll long long
const int N = 100000 + 100;
const int M = 3e6 + 1005;
typedef long long LL;


ll Qpow(ll a,ll b,ll p){
    ll ans = 1;
    a %= p;
    while(b){
        if(b & 1) ans = ans * a%p;
        b >>= 1;
        a = a * a%p;
    }
    return ans ;
}
ll prim[N],cnt[N],tot = 0;
int main(){

    ll n,mod;
    int x = 2008;
    for(int i = 2;i * i <= x;++i){  
        if(!(x%i)){
            prim[++tot] = i;
            while(!(x%i)) x /= i,cnt[tot] ++;
        }
    }
    if(x > 1) prim[++tot] = x,cnt[tot] ++;
    while(scanf("%lld%lld",&n,&mod) == 2&&n + mod){
        ll ans = 1;
        for(int i = 1; i <= tot;++i){
          ll a = ((Qpow(prim[i],cnt[i]*n+ 1,mod*(prim[i]-1)) - 1 + mod*(prim[i]-1))%(mod*(prim[i]-1)))/(prim[i]-1);
          ans = ans * a%mod;
        }
       printf("%lld\n",Qpow(2008,ans,mod));
    }
}

2、分治求等比数列的和
$Sum(p,c)=1+p+p^{2}+p^{3}+....+p^{c}$
$=(1+p+...+p^{\tfrac{c-1}{2}})+p^{\tfrac{c+1}{2}}*(1+p+...+p^{\tfrac{c-1}{2}})$
$若c为奇数=(1+p^{\tfrac{c+1}{2}})*Sum(p,\dfrac{c-1}{2})$
$若c为偶数，=(1+p^{\tfrac{c}{2}})*Sum(p,\dfrac{c}{2}-1) + p^{c}$
配合快速幂，上述分治时间复杂度 $O(log\ c)$
$AC \ Code:$

#include<iostream>
#include<cstring>
#include<queue>
#include<map>
#include<cmath>
#include<set>
#include<stack>
#include<cstdio>
#include<sstream>
#include<vector>
#include<bitset>
#include<algorithm>

using namespace std;
#define read(x) scanf("%d",&x)
#define Read(x,y) scanf("%d%d",&x,&y)
#define gc(x)  scanf(" %c",&x);
#define mmt(x,y)  memset(x,y,sizeof x)
#define write(x) printf("%d\n",x)
#define pii pair<int,int>
#define INF 0x3f3f3f3f
#define ll long long
const int N = 100000 + 100;
const int M = 3e6 + 1005;
typedef long long LL;
LL Qpow(LL a,LL b,LL p)
{
    LL res = 1%p;
    a %= p;
    while(b)
    {
        if(b&1) res =  fast_mul(res,a,p);
        b >>= 1;
        a = fast_mul(a,a,p);
    }
    return res;
}
LL Sum(LL p,LL c,LL mod)//等比数列的和
{
   // if(p == 0) return 0;
    if(c == 0) return 1;
    if(c&1) {
        return Sum(p,(c-1)/2,mod)*(1LL+Qpow(p,(c+1)/2,mod))%mod;
    }
    else {
        return (Sum(p,(c/2-1),mod)*(1LL+Qpow(p,c/2,mod))%mod+Qpow(p,c,mod))%mod;
    }

}
ll prim[N],cnt[N],tot = 0;
int main(){

    ll n,mod;
    int x = 2008;
    for(int i = 2;i * i <= x;++i){  
        if(!(x%i)){
            prim[++tot] = i;
            while(!(x%i)) x /= i,cnt[tot] ++;
        }
    }
    if(x > 1) prim[++tot] = x,cnt[tot] ++;
    while(scanf("%lld%lld",&n,&mod) == 2&&n + mod){
        ll ans = 1;
        for(int i = 1; i <= tot;++i){
          ans = ans * Sum(prim[i],cnt[i]*n,mod)%mod;
        }
       //cout<<ans<<endl;
       printf("%lld\n",Qpow(2008,ans,mod));
    }
}