朴素贝叶斯（Naive Bayes）是一种简单的分类算法。

一、朴素贝叶斯的理论基础

给定训练数据集（X,Y），其中每个样本x都包括n维特征，即x=(x1,x2,x3,…,xn)，类标记集合含有k种类别，即y=(y1,y2,…,yk)。

如果现在来了一个新样本x，我们要怎么判断它的类别？从概率的角度来看，这个问题就是给定x，它属于哪个类别的概率最大。那么问题就转化为求解P(y1|x),P(y2|x),…,P(yk|x)中最大的那个，即求后验概率最大的。

P(yk|x)根据贝叶斯定理和全概率公式可以求出。分子中的P(yk)是先验概率，根据训练集就可以简单地计算出来。
贝叶斯公式：

全概率公式：

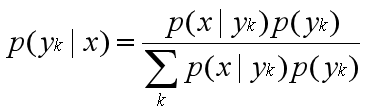
朴素贝叶斯算法对条件概率分布作出了独立性的假设，假设各个维度的特征x1,x2,…,xn互相独立。

那么条件概率公式可以化为：

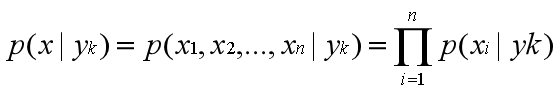
于是朴素贝叶斯分类器可表示为：

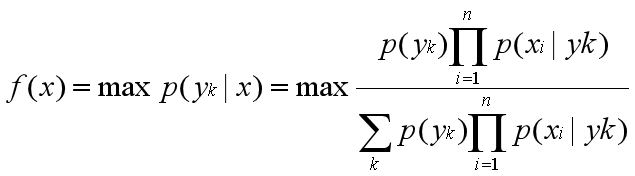
因为对所有的yk，上式中的分母的值都是一样的，所以可以忽略分母部分。朴素贝叶斯分类器最终表示为：

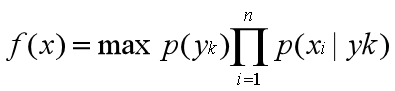
###下面举一个例子：
####数据集：

####测试集：

首先我们估计类先验概率P©，显然有

$P(好瓜 = 是) = \frac{8} {17}\approx 0.471$,
$P(好瓜 = 否) = \frac{9} {17}\approx 0.529$,

然后，为每个属性估计条件概率 $P(X_i|C):$

$P_{青绿|是} = P(色泽 = 青绿 | 好瓜 = 是) = \frac{3} {8}= 0.375$,
$P_{青绿|否} = P(色泽 = 青绿 | 好瓜 = 否) = \frac{3} {9}\approx 0.333$,
$P_{蜷缩|是} = P(根蒂 = 蜷缩 | 好瓜 = 是) = \frac{5} {8} = 0.625$,
$P_{蜷缩|否} = P(根蒂 = 蜷缩 | 好瓜 = 否) = \frac{3} {9}\approx 0.333$,
$P_{浊响|是} = P(敲声 = 浊响 | 好瓜 = 是) = \frac{6} {8} = 0.750$,
$P_{浊响|否} = P(敲声 = 浊响 | 好瓜 = 否) = \frac{4} {9}\approx 0.444$,
$P_{清晰|是} = P(纹理 = 清晰 | 好瓜 = 是) = \frac{7} {8} = 0.875$,
$P_{清晰|否} = P(纹理 = 清晰 | 好瓜 = 否) = \frac{2} {9}\approx 0.222$,
$P_{凹陷|是} = P(脐部 = 凹陷 | 好瓜 = 是) = \frac{6} {8} = 0.750$,
$P_{凹陷|否} = P(脐部 = 凹陷 | 好瓜 = 否) = \frac{2} {9}\approx 0.222$,
$P_{硬滑|是} = P(触感 = 硬滑 | 好瓜 = 是) = \frac{6} {8} = 0.750$,
$P_{硬滑|否} = P(触感 = 硬滑 | 好瓜 = 否) = \frac{6} {9}\approx 0.667$,
$P_{密度:0.697|是} = P(密度 = 0.697 | 好瓜 = 是) = \frac{1}{\sqrt{2\pi}\cdot0.129}exp(-\frac{(0.697-0.574)^2}{2\cdot0.129^2})\approx1.959$,
$P_{密度:0.697|否} = P(密度 = 0.697 | 好瓜 = 否) = \frac{1}{\sqrt{2\pi}\cdot0.195}exp(-\frac{(0.697-0.496)^2}{2\cdot0.0.195^2})\approx1.203$,
$P_{含糖率:0.460|是} = P(含糖率 = 0.460 | 好瓜 = 是) = \frac{1}{\sqrt{2\pi}\cdot0.101}exp(-\frac{(0.460-0.279)^2}{2\cdot0.101^2})\approx0.788$,
$P_{含糖率:0.460|否} = P(含糖率 = 0.460 | 好瓜 = 否) = \frac{1}{\sqrt{2\pi}\cdot0.108}exp(-\frac{(0.460-0.154)^2}{2\cdot0.108^2})\approx0.066$.

于是，有：
$P(好瓜 = 是) \times P_{青绿|是} \times P_{蜷缩|是} \times P_{浊响|是} \times P_{清晰|是} \times P_{凹陷|是} \times P_{硬滑|是} \times P_{密度:0.697|是} \times P_{含糖:0.460|是}\approx0.063$

$P(好瓜 = 否) \times P_{青绿|否} \times P_{蜷缩|否} \times P_{浊响|否} \times P_{清晰|否} \times P_{凹陷|否} \times P_{硬滑|否} \times P_{密度:0.697|否} \times P_{含糖:0.460|否}\approx6.80\times10^{-5}$

由于 0.063 > $6.80\times10^{-5}$， 因此，朴素贝叶斯分类器将测试样本“测1”判别为“好瓜”

二、三种常见模型

2.1.1多项式模型
当特征是离散的时候，使用多项式模型。多项式模型在计算先验概率P(yk)和条件概率P(xi|yk)时，会做一些平滑处理，具体公式为：

N是总的样本个数，k是总的类别个数，Nyk是类别为yk的样本个数，α是平滑值。

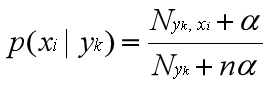
Nyk是类别为yk的样本个数，n是特征的维数，Nyk,xi是类别为yk的样本中，第i维特征的值是xi的样本个数，α是平滑值。

当α=1时，称作Laplace平滑，当0<α<1时，称作Lidstone平滑，α=0时不做平滑。如果不做平滑，当某一维特征的值xi没在训练样本中出现过时，会导致P(xi|yk)=0，从而导致后验概率为0。加上平滑就可以克服这个问题。
2.1.2编程实现：

import numpy as np
class MultinomialNB(object):
    def __init__(self,alpha=1.0,fit_prior=True,class_prior=None):
        self.alpha = alpha
        self.fit_prior = fit_prior
        self.class_prior = class_prior
        self.classes = None
        self.conditional_prob = None
	# 计算条件概率        
    def _calculate_feature_prob(self,feature):
        values = np.unique(feature) # 去除数组中的重复数字，并进行排序之后输出
        total_num = float(len(feature))
        value_prob = {}
        for v in values:
        	# np.equal([2, 3, 4], [2])，返回 [Ture, False , False]
        	# 做Laplace平滑
            value_prob[v] = (( np.sum(np.equal(feature,v)) + self.alpha ) /( total_num + len(values)*self.alpha))
        return value_prob

    def fit(self, X, y):
        self.classes = np.unique(y)
        # calculate class prior probabilities: P(y=ck)
        if self.class_prior == None:
            class_num = len(self.classes) # 类数
            if not self.fit_prior:
                self.class_prior = [1.0 / class_num for _ in range(class_num)]  # uniform prior
            else:
                self.class_prior = []
                sample_num = float(len(y)) # 样本数
                for c in self.classes:
                    c_num = np.sum(np.equal(y, c)) 
                    self.class_prior.append((c_num + self.alpha) / (sample_num + class_num * self.alpha)) # P(c)
        self.conditional_prob = {}  # like { c0:{ x0:{ value0:0.2, value1:0.8 }, x1:{} }, c1:{...} }
        for c in self.classes:
            self.conditional_prob[c] = {}
            for i in range(len(X[0])):  # for each feature
                feature = X[np.equal(y, c)][:, i] # 提取出True对应的样本的第i个特征
                self.conditional_prob[c][i] = self._calculate_feature_prob(feature)
        return self

    def _get_xj_prob(self, values_prob, target_value):
        return values_prob[target_value]
        
    def _predict_single_sample(self,x):
	    label = -1
	    max_posterior_prob = 0
	    #for each category, calculate its posterior probability: class_prior * conditional_prob
	    for c_index in range(len(self.classes)):
	        current_class_prior = self.class_prior[c_index]
	        current_conditional_prob = 1.0
	        feature_prob = self.conditional_prob[self.classes[c_index]]
	        j = 0
	        for feature_i in feature_prob.keys():
	            current_conditional_prob *= self._get_xj_prob(feature_prob[feature_i],x[j])
	            j += 1
	
	        #compare posterior probability and update max_posterior_prob, label
	        if current_class_prior * current_conditional_prob > max_posterior_prob:
	            max_posterior_prob = current_class_prior * current_conditional_prob
	            label = self.classes[c_index]
	    return label
		 
    def predict(self,X):
	    if X.ndim == 1:
	        return self._predict_single_sample(X)
	    else:
	        #classify each sample
	        labels = []
	        for i in range(X.shape[0]):
	                label = self._predict_single_sample(X[i])
	                labels.append(label)
	        return labels

if __name__ == "__main__":
    X = np.array([
        [1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3],
        [4, 5, 5, 4, 4, 4, 5, 5, 6, 6, 6, 5, 5, 6, 6]
    ])
    X = X.T
    y = np.array([-1, -1, 1, 1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, -1])

    nb = MultinomialNB(alpha=1.0, fit_prior=True)
    nb.fit(X, y)
    print(nb.predict(np.array([2, 4])))  # 输出-1
	

2.2.1高斯模型

当特征是连续变量的时候，运用多项式模型就会导致很多P(xi|yk)=0（不做平滑的情况下），此时即使做平滑，所得到的条件概率也难以描述真实情况。所以处理连续的特征变量，应该采用高斯模型

高斯模型假设每一维特征都服从高斯分布（正态分布）：

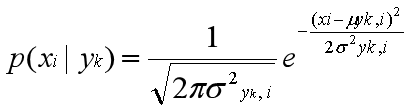
μyk,i表示类别为yk的样本中，第i维特征的均值。
σ2yk,i表示类别为yk的样本中，第i维特征的方差。

2.2.2编程实现

class GaussianNB(MultinomialNB):
        #calculate mean(mu) and standard deviation(sigma) of the given feature
        def _calculate_feature_prob(self,feature):
                mu = np.mean(feature)
                sigma = np.std(feature)
                return (mu,sigma)

        #the probability density for the Gaussian distribution 
        def _prob_gaussian(self,mu,sigma,x):
                return ( 1.0/(sigma * np.sqrt(2 * np.pi)) *
                        np.exp( - (x - mu)**2 / (2 * sigma**2)) )

        #given mu and sigma , return Gaussian distribution probability for target_value
        def _get_xj_prob(self,mu_sigma,target_value):
                return self._prob_gaussian(mu_sigma[0],mu_sigma[1],target_value)

2.3.1伯努利模型

与多项式模型一样，伯努利模型适用于离散特征的情况，所不同的是，伯努利模型中每个特征的取值只能是1和0(以文本分类为例，某个单词在文档中出现过，则其特征值为1，否则为0).伯努利模型中，条件概率P(xi|yk的计算方式是：当特征值xi为1时，P(xi|yk)=P(xi=1|yk)；当特征值xi为0时，P(xi|yk)=1−P(xi=1|yk)