图论部分的的知识，笔者在本科信科阶段的学习中，已经在《离散数学》、《运筹学》、《数据结构》科目中有所学习，但是所学图论知识相对零散；不成体系。经过一段时间梳理学习,笔者在此将学习所得整理成博客，以便于将来的温习。不足之处望读者多加指正。

图的遍历搜索

关于图基本知识笔者在此不做赘述，笔者主要所写内容主要是图的算法思想、实现程序与算法的优劣分析。

DFS（深度优先搜索）

算法思想

从某个点一直往深处走，走到不能往下走之后，就回退到上一步，直到找到解或把所有点走完。

算法步骤（递归或栈实现）

1.访问指定起始地点。

2.若当前访问顶点的邻接顶点有未被访问的顶点，就任选一个访问。如果没有就3.回退到最近访问的顶点，直到与起始顶点相通的所有点被遍历完。

3.若途中还有顶点未被访问，则再选一个点作为起始顶点。重复步骤2（针对非连通图）。

实现程序

# 将图以字典的存储
def DFS(graph,s):
    stack=[]
    stack.append(s)
    seen=set()
    seen.add(s)
    print('深度优先搜索的结果是：', end=' ')
    while(len(stack)>0):
        vertex=stack.pop(0)
        nodes=graph[vertex]
        for w in nodes:
            if w not in seen:
                stack.append(w)
                seen.add(w)
                # 1.将点放入队列
                # 2.如果队列非空，将队列点取出，同时将其Key只取出，如果Key没有在seen中加入seen，同时加入队列
        print(vertex,end='')
    print()
# DFS(graph,"A")

BFS（广度优先搜索）

算法思想

从某个点一直把其邻接点走完，然后任选一个邻接点把与之邻接的未被遍历的点走完，如此反复走完所有结点。类似于树的层序遍历。

算法步骤（用队列实现）

1.访问指定起始点。

2.访问当前顶点的邻接顶点有未被访问的顶点，并将之放入队列中。

3.删除队列的队首节点。访问当前队列的队首，重复步骤2。直到队列为空。

4.若途中还有顶点未被访问，则再选一个点作为起始顶点。重复步骤2。（针对非连通图）。

实现程序

rom Circular_queue import Queue
# 将图以字典的存储
def BFS(graph,s):
    queue=Queue()
    queue.offer(s)
    seen=set()
    seen.add(s)
    print('广度优先搜索的结果是：',end=' ')
    while(queue.lenth()>0):
        vertex=queue.poll()
        nodes=graph[vertex]
        for w in nodes:
            if w not in seen:
                queue.offer(w)
                seen.add(w)
                # 1.将点放入队列
                # 2.如果队列非空，将队列点取出，同时将其Key只取出，如果Key没有在seen中加入seen，同时加入队列
        print(vertex,end='')
    print()
# BFS(graph,"A")

引用的queue包

class Queue():
    def __init__(self):
        self.Maxsize=7
        self.qE=[None]*self.Maxsize
        self.front=0#队首
        self.rear=0#队尾
        # 定义一个长度为6的循环队列

    def isEmpty(self):
        return self.front==self.rear
    #判断是否为空队列

    def lenth(self):
        return (self.rear-self.front+7)%7
    #返回队列长度

    def offer(self,x):
        if(self.rear+1)%self.Maxsize==self.front:
            raise Exception("队列满了")
        self.qE[self.rear]=x
        self.rear=(self.rear+1)%self.Maxsize
        #x入队

    def poll(self):
        if self.isEmpty():
            raise Exception("队列是空的")
        p=self.qE[self.front]
        self.front=(self.front+1)%self.Maxsize
        #print('队首元素%d出列'%(p))
        return p
        #队首出队

    def disploy(self):
        for i in range(self.front,self.rear):
            print(self.qE[i],end=' ')
        #将队列元素全部输出
# q=Circular_queue()
# q.offer(2)
# q.offer(3)
# q.poll()

算例

import numpy as np
from DFS import DFS
from BFS import BFS
e=np.array([[0,1,1,0,0,0],[0,0,1,1,0,0],[0,0,0,0,1,0],[0,0,1,0,1,1],[0,0,0,0,0,0],[0,0,0,0,0,0]])
# 定义其邻接矩阵
X=ord('A')
graph={'A':[],
       'B':[],
       'C':[],
       'D':[],
       'E':[],
       'F':[]
        }
chudu=[0]*6
rudu=[0]*6
for i in range(6):
    for j in range(6):
        if e[i][j]==1:
            graph[chr(X+i)].append(chr(X+j))
            chudu[i] += 1
            rudu[j] += 1
for i in range(6):
    print('%s的出度为：%d，入度为：%d'%(chr(X+i),chudu[i],rudu[i]))
# 计算节点的出度与入度

# 将邻接矩阵转化成邻接表的形式
# graph['A'].append(chr(A))
# print(graph)
# print('深度优先搜索的结果是：ABDFEC')
print(graph)
DFS(graph,'A')
BFS(graph,'A')
# print(e)

问题：给出一个有向图的邻接矩阵形式，给出图的各节点的出入度、与DFS、BFS下的遍历。结果：

BFS复杂度分析

BFS是一种借用队列来存储的过程，分层查找，优先考虑距离出发点近的点。无论是在邻接表还是邻接矩阵中存储，都需要借助一个辅助队列，v个顶点均需入队，最坏的情况下，空间复杂度为O（v）。
邻接表形式存储时，每个顶点均需搜索一次，时间复杂度T1=O（v），从一个顶点开始搜索时，开始搜索，访问未被访问过的节点。最坏的情况下，每个顶点至少访问一次，每条边至少访问1次，这是因为在搜索的过程中，若某结点向下搜索时，其子结点都访问过了，这时候就会回退，故时间复 杂度为O(E)，算法总的时间复 度为O(|V|+|E|)。
邻接矩阵存储方式时，查找每个顶点的邻接点所需时间为O(V)，即该节点所在的该行该列。又有n个顶点，故算总的时间复杂度为O(|V|^2)。

DFS复杂度分析

DFS算法是一一个递归算法，需要借助一个递归工作栈，故它的空问复杂度为O(V）。
遍历图的过程实质上是对每个顶点查找其邻接点的过程，其耗费的时间取决于所采用结构。
邻接表表示时，查找所有顶点的邻接点所需时间为O(E)，访问顶点的邻接点所花时间为O（V）,此时，总的时间复杂度为O(V+E)。
邻接矩阵表示时，查找每个顶点的邻接点所需时间为O(V)，要查找整个矩阵，故总的时间度为O(V^2)。
v为图的顶点数，E为边数。

最小生成树

建模中，最小生成树常被用在一些运筹规划的问题中；最常见的有如周游世界等。

Prim算法

算法思想与步骤

1).输⼊：⼀个加权连通图，其中顶点集合为V，边集合为E；

2).初始化：Vnew = {x}，其中x为集合V中的任⼀节点（起始点），Enew = {},为空；

3).重复下列操作，直到Vnew = V： a.在集合E中选取权值最⼩的边<u, v>，其中u为集合Vnew中的元素，⽽v 不在Vnew集合当中，并且v∈V（如果存在有多条满⾜前述条件即具有相同 权值的边，则可任意选取其中之⼀）； b.将v加⼊集合Vnew中，将<u, v>边加⼊集合Enew中；

4).输出：使⽤集合Vnew和Enew来描述所得到的最⼩⽣成树。

算法分析

这⾥记顶点数v，边数e
对于邻接矩阵算法复杂度为:O(v2)
对于邻接表算法复杂度为:O(elog2v)

Kruskal算法

算法思想与步骤

1).记Graph中有v个顶点，e个边

2).新建图Graphnew，Graphnew中拥有原图中相同的e个顶点，但没有边

3).将原图Graph中所有e个边按权值从⼩到⼤排序

4).循环：从权值最⼩的边开始遍历每条边 直⾄图Graph中所有的节点都在同⼀ 个连通分量中 if 这条边连接的两个节点于图Graphnew中不在同⼀个连通分量中 添加这条边到图Graphnew中

两算法间的异同

从策略上来说，Prim算法是直接查找，多次寻找邻边的权重最⼩值，⽽Kruskal 是需要先对权重排序后查找的～ 所以说，Kruskal在算法效率上是⽐Prim快的，因为Kruskal只需⼀次对权重的排 序就能找到最⼩⽣成树，⽽Prim算法需要多次对邻边排序才能找到～

算例

建模过程以Kruskal算法为例

实现程序

a=zeros(6);%邻接矩阵初始化
a(1,[2:6])=[56 35 21 51 60];
a(2,[3:6])=[21 57 78 70];
a(3,[4:6])=[36 68 68];
a(4,[5:6])=[51 61];
a(5,6)=13;
a=a';
a=sparse(a);%变化成下三角矩阵
[ST,pred]=graphminspantree(a,'method','Kruskal')%调用工具箱求得最小生成树
nodestr=['L','M','N','Pa','T'];%输入顶点名称的字符细胞组
h=view(biograph(ST,nodestr,'ShowArrows','off','ShowWeight','on'))
h.EdgeType='segmented';%边连接成线段
h.LayoutType='equilibrium';
dolayout(h)%设置图形布局属性并刷新图形布局

算例结果

图论的问题利用Matlab进行求解更加简便直观

最短路

在建模中，最短路常求解带权图两点的最短路径，常用算法有

Dijkstria算法

算法思想与步骤

1.将图上的初始点看作⼀个集合S，其它点看作另⼀个集合

2.根据初始点，求出其它点到初始点的距离d[i] （若相邻，则d[i]为边权值；若 不相邻，则d[i]为⽆限⼤）

3.选取最⼩的d[i]（记为d[x]），并将此d[i]边对应的点（记为x）加⼊集合S （实际上，加⼊集合的这个点的d[x]值就是它到初始点的最短距离）

4.再根据x，更新跟 x 相邻点 y 的d[y]值：d[y] = min{ d[y], d[x] + 边权值w[x] [y] }，因为可能把距离调⼩，所以这个更新操作叫做松弛操作。

5.重复3，4两步，直到⽬标点也加⼊了集合，此时⽬标点所对应的d[i]即为最 短路径⻓度

Floyd算法

算法思想与步骤

这个算法简单来说就是利⽤动态规划进⾏批量处理。它具有⾼效，代码简短的优 势，⽐较常⽤
我们⽤dp[ k ][ i ][ j ]表示i到j能经过1 ~ k的点的最短路。 那么实际上dp[ 0 ][ i ][ j ]就是原图，如果i, j之间存在边，那么i, j之间不经过任何点 的最短路就是边⻓
否则，i, j之间的最短路为⽆穷⼤
所以就有转移⽅程
dp[ k ][ i ][ j ] = min(dp[ k - 1 ][ i ][ j ], dp[ k - 1 ][ i ][ k ] + dp[ k - 1 ][ k ][ j ])
我们再分析就会发现，dp[k] 只能由 dp[k - 1]转移⽽来。
所以，状态转移⽅程可以进⼀步简化为 dp[ i ][ j ] = min(dp[ i ][ j ], dp[ i ][ k ] + dp[ k ][ j ]);

算例

算例程序

clc,
clear
a=zeros(5);%邻接矩阵初始化
a(1,[2:5])=[0.8 2 3.8 6];
a(2,[3:5])=[0.9 2.1 3.9];
a(3,[4:5])=[1.1 2.3];
a(4,5)=1.4;
b=sparse(a);
[dist,path]=graphshortestpath(b,1,5,'Directed',1)%调用工具箱求最短路
%调用模型为dist最短路长度，path最短路长度
% 这里直接用最小生成树方法来生成图似乎不通？？？？
% nodestr=['1','2','3','4'];%输入顶点名称的字符细胞组
% h=view(biograph(dist,nodestr,'ShowArrows','off','ShowWeight','on'))
% h.EdgeType='segmented';%边连接成线段
% h.LayoutType='equilibrium';
%dolayout(h)%设置图形布局属性并刷新图形布局
h=view(biograph(b,[],'showW','on'));
edges=getedgesbynodeid(h,get(h.Nodes(path),'ID'));
set(h.Nodes(path),'color',[1 0 0])

以Dilkstria算法求解为例

算例结果

最短路为1 2 3 5即前三年机器都更换

最大流最小割

由于笔者学艺稍逊，同时建模中问题求最大流居多，因此，笔者再此介绍最大流解题思想.

算法思想与步骤

最大流思想
最大流的三个常用算法

算例

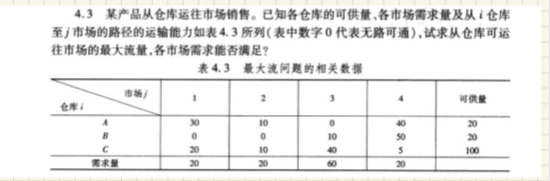
对于最大流问题，一般在建模过程加入S点作为流出点（源点）t点作为流入点（终点）构造成一个最大流问题。

算例程序

clc,
clear
a=zeros(9);
a(1,[2:4])=[20 20 100];%构造带权邻接矩阵
a(2,[5 6 8])=[30 10 40];
a(3,[7 8])=[10 50];
a(4,[5:8])=[20 10 40 5];
a([5:8],9)=[20 20 60 20];
a=sparse(a);
[M,F,K]=graphmaxflow(a,1,9)%b为manflow、c为最大流对应的带权矩阵，d是最小割
%尝试调用biograph进行形象的画图
% View graph with original flows
h = view(biograph(a,[],'ShowWeights','on'))
% View graph with actual flows
view(biograph(F,[],'ShowWeights','on'))
% Show in the original graph one solution of the mincut problem
set(h.Nodes(K(1,:)),'Color',[1 0 0])

计算结果

左图为最大流对应的解的带权有向图右图为原来图做完最小割后的情形。

最小费用最大流

笔者校赛建模曾是论文主笔，做的赛题便是上述类型，基本套路是先对问题进行最大流求解，在建立数学模型计算出最小费用，详细的讲解可以该类型的建模优秀论文进行参阅。

算例

程序

首先对其进行最大流求解，可得最大流为15

clc,
clear
a=zeros(7);
a(1,[2:3])=[8 7];%构造带权邻接矩阵
a(2,[4:6])=[8 8 8];
a(3,[4:6])=[8 8 8];
a([4:6],7)=[4 5 6];
a=sparse(a);
[M,F,K]=graphmaxflow(a,1,7)%M为manflow、F为最大流对应的带权矩阵，K是最小割
%尝试调用biograph进行形象的画图
nodestr=['S','A','B','1','2','3','t' ]
% View graph with original flows
h = view(biograph(a,[],'ShowWeights','on'))
% View graph with actual flows
view(biograph(F,[],'ShowWeights','on'))
% Show in the original graph one solution of the mincut problem
set(h.Nodes(K(1,:)),'Color',[1 0 0])
h=view(biograph(F,nodestr,'ShowWeight','on'))
%dolayout(h)%设置图形布局属性并刷新图形布局

随后使用lingo进行最小费用的求解得最小费用为240

model:
sets:
nodes/s,a,s,b,a l,a 2，b1,b2,b3,1 t,2 t,3 t/:b,c,f:
endsets:
data:
b=0 0 20 24 5 30 22 20 0 0 0;
c=8 7 8 8 8 7 7 7 4 5 6;
d=15 0 0 0 0 0 -15;
enddata
n=@size(nodes);
min=@sum(arcs:b*f);
@for(node(i):@sum(arcs(i,j):f(i,j))-@sum(arcs(j,i):f(j,i))=d(i));
@for(arcs:@bnd(0,f,c));
end

运行结果

总结

经过本次梳理，发觉：建模知我长短，而我却不晓建模深浅。
几个遗留问题：最大流算法的算法原理与分析。
最大流最小费用在求最小费用时的数学模型建立。
收获：matlab几个常用图论包的调用，和与图论有关的作图工具箱的使用biography函数的使用