目的

在数字设备上绘制一条直线，其过程为给定直线的起点和终点，在光栅显示器的二维点阵中确定一组点最佳逼近所给直线。
绘制直线的本质是确定点序列。

数值微分法（DDA）

算法原理

直线的一阶导数连续，对应微分增量成比例，可以使用当前位置 $(x_i,y_i)$分别加上两个小增量 $\varepsilon*\Delta x$与 $\varepsilon*\Delta y$即可求出相应的 $(x_{i+1},y_{i+1})$（ $\varepsilon$取值极小），即：
$y_{i+1}=y_i+\varepsilon*\Delta y$
$x_{i+1}=x_i+\varepsilon*\Delta x$
相应的直线的斜率为：
$\frac{dy}{dx}=\frac{\Delta y}{\Delta x}=\frac{Y_1-Y_0}{X_1-X_0}=k$

近似拟合

由于在实际的机器中我们无法实现那么高的精度，所以我们选择 $\varepsilon=\frac{1}{max(|\Delta x|,|\Delta y|)}$，将对应的 $\varepsilon*\Delta x$或 $\varepsilon*\Delta y$变为单位步长，对应有不同斜率有两种情况：
一种情况为： $max(|\Delta x|,|\Delta y|)=|\Delta x|$，即 $|k|<=1$。
$y_{i+1}=y_i+\varepsilon*\Delta y=y_i+\frac{1}{|\Delta x|}*\Delta y=y_i\pm k$
$x_{i+1}=x_i+\varepsilon*\Delta x=x_i+\frac{1}{|\Delta x|}*\Delta x=x_i\pm 1$

另一种情况为： $max(|\Delta x|,|\Delta y|)=|\Delta y|$，即 $|k|>=1$。
$y_{i+1}=y_i+\varepsilon*\Delta y=y_i+\frac{1}{|\Delta y|}*\Delta y=y_i\pm 1$
$x_{i+1}=x_i+\varepsilon*\Delta x=x_i+\frac{1}{|\Delta y|}*\Delta x=x_i\pm \frac{1}{k}$

由于在绘制时设备无法绘制半个像素，所以需要对x，y进行四舍五入取整，实现为：
$x_i=(int)(x_i+0.5)$， $y_i=(int)(y_i+0.5)$

代码实现

void DDA(int x0,int x1,int y0,int y1)
{
	int dx.dy,epsl,k;
	float x,y,xIncre,yIncre;
	dx=x1-x0;
	dy=y1-y0;
	x=x0;
	y=y0;
	if(abs(dx)>abs(dy)){//对应|k|与1比较
		epsl=abs(dx);
	}else{
		epsl=abs(dy);
	}
	xIncre=(float)dx/(float)epsl;
	yIncre=(float)dy/(float)epsl;
	for(k=0;k<=epsl;k++){
		drawPixel((int)(x+0.5),(int)(y+0.5));
		x+=xIncre;
		y+=yIncre;
	}
}

在迭代中，对应新的x，y的值都是以前一步的值加上一个增量获得的，对应代码中的x+=xIncre与y+=yIncre，这种表示的算法为一个增量算法。算法简单，易于实现。

评价

优点：算法直观，易于实现。
缺点：涉及浮点数运算，不利于硬件实现。

中点Bresenham算法

算法原理

对于相应直线的斜率有：
$\frac{\Delta y}{\Delta x}=\frac{Y_1-Y_0}{X_1-X_0}=k$
直线方程有 $f(x,y)=y-kx-b$
相应的在图像上可以将平面划分为三个部分，分别为 $f(x,y)=0,f(x,y)>0,f(x,y)<0$

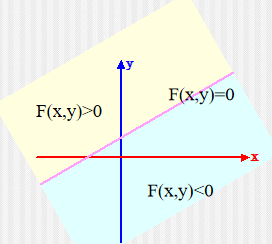
这里我们仅考虑 $0<k<1$的情况，所以对于x方向的增量(增量取1)，产生的y只有两个可能的点(x+1，y)，或者(x+1,y+1)，我们以两点之间的中点来进行评判，即(x+1,y+0.5)。对于实际的直线f(x,y),我们将中点带入有：d=f(x+1,y+0.5)，如果其值大于0，说明对应直线在中点下方，所以应该取(x+1，y)，若值小于0，说明对应直线在中点上方，所以应该取(x+1，y+1)，即：
$y=y+1 (d<0)$
$y=y (d \geq 0)$

误差迭代

对于相应产生误差d，根据之前产生的误差的取值有两种取值方式：
当d小于0时，上次对应取的点为f(x+1,y+1)，所以这次我们判断的中点为f(x+2,y+1.5)。
对应的结果为 $d_{i+1}=f(x+2,y+1.5)=y+1.5-k(x+2)-b=y+0.5-k(x+1)-b-k=d_i-k+1$
对应误差的增量为 $1-k$

当d大于0时，上次对应取的点为f(x+1,y)，所以这次我们判断的中点为f(x+2,y+0.5)。
对应的结果为 $d_{i+1}=f(x+2,y+0.5)=y+0.5-k(x+2)-b=y+0.5-k(x+1)-b-k=d_i-k$
对应误差的增量为 $-k$

误差的初值为对应(x,y)取 $(x_0,y_0)$,中点为 $(x_0+1,y_0+0.5)$， $d_{0}=f(x_0+1,y_0+0.5)$
对应 $f(x_0,y_0)=0=y_0-kx_0-b$，所以有 $d_0=0.5-k$
展开一下有 $d_0=0.5-\frac{\Delta y}{\Delta x}$，即为 $2\Delta xd_0=\Delta x-2\Delta y$
将相应的 $d_0=2\Delta xd_0$，对应的增量也对应乘以 $2\Delta x$为 $-k*2\Delta x=-2\Delta y$与 $(1-k)*2\Delta x=2\Delta x-2\Delta y$

代码实现

void MidBresenham(int x0,int x1,int y0,int y1){
	int dx,dy,d,UpIncre,DownIncre,x,y;
	if(x0>x1){
		x=x1;
		x1=x0;
		x0=x;
		y=y1;
		y1=y0;
		y0=y;
	}
	x=x0;
	y=y0;
	dx=x1-x0;
	dy=y1-y0;
	d=dx-2*dy;
	UpIncre=2*dx-2*dy;
	DownIncre=(-2)*dy;
	while(x<=x1){
		drawPixel(x,y);
		x++;
		if(d<0){
			y++;
			d+=UpIncre;
		}else{
			d+=DownIncre;
		}
	}
}

对应 $k>1$时将对应的x与y互换即可，如果斜率为负值，将对应其中一个坐标改增量为减即可，其余的操作均是相同的。同时避免了除法运算的问题。