题目地址: http://poj.org/problem?id=2955

题目内容:

Description

Input

Output

Sample Input

((()))
()()()
([]])
)[)(
([][][)
end

Sample Output

6
6
4
0
6

　　在我第一次遇到这题时，我尝试用栈来做，结果怎么也做不出来......实际上，这题应该用动态规划来做。

　　在讲这题之前，先弄明白“子序列”和“子字符串”这两个概念。

　　所谓子字符串，就是在一个字符串里取其中的一段，这一段就叫做子字符串。比如在字符串“abcdefg”中取一段“bcde”，“bcde”就是“abcdefg”的子字符串。子字符串中的所有字符在原字符串中的位置都是连续的，在中间不能断开，否则就不叫子字符串，而是叫子序列。比如，“bcdg”就不是“abcdefg”的子字符串，但它是子序列。子序列可以是断开的，也可以是不断开的，但是子字符串不可以是断开的。所以子字符串都属于子序列。
　　
　　题目中的要求就是要我们从一个由括号组成的字符串中，找出该字符串中的一个括号全部匹配的子序列，使得该子序列是所有括号全部匹配的子序列中最长的，而这个最长的子序列的长度就是我们需要输出的答案。

　　根据动态规划的思想，我们首先要做的是把大问题分解为小问题。这里的大问题就是要求出一串字符串的最长匹配子序列的长度，我们自然可以想到，小问题就是求出字符串的一段较短的子字符串的最长匹配子序列的长度。对于长度为1和2的子字符串，我们直接很容易就可以得到相应的子序列的长度。那么，如何利用长度为1和2的子字符串来推算出长度为3，4，5......的子字符串的最长匹配子序列的长度呢？

　　我们定义一个函数dp(x,y)，这个函数的值为从下标x开始到下标y为止对应的子字符串的最长匹配子序列的长度。显然，所有长度为1的子字符串的dp值都为0。除了“()”和“[]”对应的dp值为2外，所有长度为2的子字符串的dp值也为0。

　　接下来假设我们要求一段长度大于2的子字符串s的dp值，s的第一个字符的下标为x，最后一个字符的下标为y，并且s的所有子字符串(不包括s本身)的dp值都是已知的。那么我们要怎么求呢？请思考一下。

　　在这里,s的dp值跟它的子字符串的dp值之间的关系并不太简单，并不是用一个简单的式子就能表示的。我们需要用到枚举的思路，把s中所有可能满足条件的子序列都枚举出来，找到其中最长的一条子序列，那么这条最长的子序列的长度就是s的dp值。下面讲讲具体应该怎么枚举。

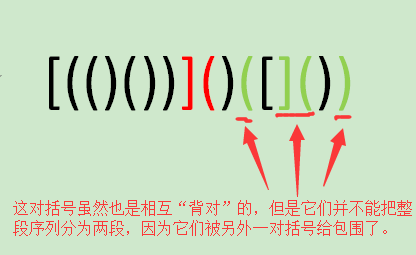
　　在s的最长匹配子序列中，有可能存在这样的一对括号：这对括号的位置相邻，而且它们是相互“背对”的，比如“)(”、“][”、“)[”、“](”，并且它们没有被任何其他括号给包围。这样的一对括号能够把最长匹配子序列分为两段。如下图所示。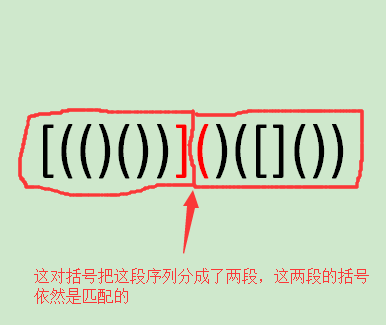

 

　　这样一对特殊的括号就是我们求s的dp值过程中的关键之一。如果我们能够找到一个数k，使得这对特殊括号的左边那个括号的下标小于等于k，右边的括号大于等于k + 1，那么s的dp值不就等于dp(x,k) + dp(k + 1,y)了吗？但是我们要怎么找到这个数k呢？那就只能靠枚举啦！我们依次令k等于x,x + 1,x + 2,......,y - 1，并求出所有dp(x,k) + dp(k + 1,y)的值，最后取最大值即可。

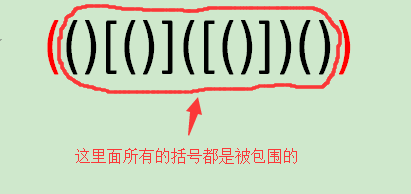
　　这时有的小伙伴可能就会发问了，如果s的最长匹配子序列内部所有括号都是被包围的，我们就找不到上面所说的那对特殊括号了，这时候该怎么办？



　　这个不成问题，我们在枚举k的过程中，有可能会使得最长匹配子序列中所有括号的下标都小于等于k或者大于等于k，这时我们依然能够求得s的dp值。

　　“但是如果那两个最外围的括号的下标恰好分别是x和y，你这样枚举k可就算不出来正确的dp值了！”

　　这样的话问题就更简单了，s的dp值直接就等于2 + dp(x + 1,y - 1)。

　　综上，我们只要把dp(x,k)+dp(k + 1,y)(k = x,x + 1,x + 2,......,y - 1)的值都枚举出来，并且在s的两端的括号匹配时，把2 + dp(x + 1,y - 1)也枚举出来，取这些值中的最大值为s的dp值，那么就能求得s的最长匹配子序列的长度。

　　所以，这道题的求解过程应该是这样的：先把字符串的所有长度为1和2的子字符串的dp值求出来，然后用之前所说的方法，利用长度为1和2的子字符串的dp值求出长度为3的子字符串的dp值，进而求出长度为4,5,6......的子字符串的dp值，最后就能求得整个字符串的dp值了，整个字符串的dp值就是我们所要的答案。

　　接下来上代码，结束。

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int SIZE = 110;
char str[SIZE];
int dp[SIZE][SIZE];

int getLength(char* str,int upper)
{
    //因为数组dp是定义在全局作用域中的，其内部元素的初始值都为0，故这里直接求长度为2的子字符串的dp值即可。
    for(int i = 0;i <= upper - 1;++i)
    {
        if((str[i] == '(' && str[i + 1] == ')') || (str[i] == '[' && str[i + 1] == ']'))
        {
            dp[i][i + 1] = 2;
        }
    }

    for(int gap = 2;gap <= upper;++gap)
    {
        for(int i = 0;i <= upper - gap;++i)
        {
            if((str[i] == '(' && str[i + gap] == ')') || (str[i] == '[' && str[i + gap] == ']'))
            {
                dp[i][i + gap] = max(dp[i][i + gap],2 + dp[i + 1][i + gap -1]);
            }
            for(int j = i;j <= i + gap - 1;++j)
            {
                dp[i][i + gap] = max(dp[i][i + gap],dp[i][j] + dp[j + 1][i + gap]);
            }
        }
    }

    return dp[0][upper];
}

int main()
{
    while(scanf("%s",str) && strcmp(str,"end") != 0)
    {
        printf("%d\n",getLength(str,strlen(str) - 1));
        memset(dp,0,sizeof(dp));
    }
}