声明：本博客所有随笔都参照了网络资料或其他博客，仅为博主想加深理解而写，如有疑问欢迎与博主讨论✧｡٩(ˊᗜˋ)و✧*｡

割点

概念

在一个无向图中，将某一个点以及此点所连的所有的边去掉，剩下的点不再全部连通，那么这个点就叫做割点

tarjan算法

强连通分量中也有个叫 \(tarjan\) 的算法，因为是由同一个人发明出来的，至于这俩算法有没有关联，等后面再谈

首先我们要把整个图变成一颗 \(dfs\) 树

（至于为什么要变成一棵树，我想过了但是没有想出来，也许只是为了方便后续操作？如果有知道的小伙伴可以分享一下ヾ(๑╹◡╹)ﾉ"）

随意选择一个点作为根，从根节点往下搜索，每个搜到的节点打个标记，若搜索过程中碰到已打过标记的点则回溯，最后就搜出一颗 \(dfs\) 树了

例如这样的一张图：

我们选定 \(1\) 为根节点，做一颗 \(dfs\) 树，即为：

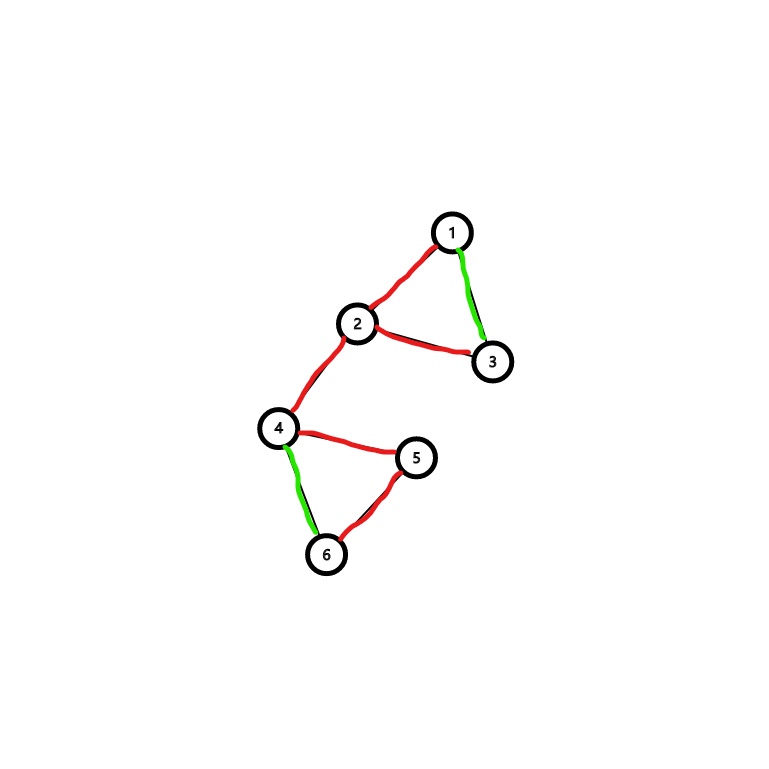
红色的边即为树边，绿色的边为回边（前向边/返祖边），通过回边可以去往之前到过的点

对于根来说很好判断，只要有两个或以上的子树就为割点，因为去掉之后子树间不可能连通

对于子树中的点，我们记录两个值: \(dfn[i]\) 和 \(low[i]\) ，\(dfn[i]\) 表示在 \(dfs\) 树中的编号，\(low[i]\) 表示当前点及其子树中所有的节点，通过回边所连的点中的最小编号（貌似有点绕，要多读几遍）

对于一条边 \((u, v)\) 来说，如果 \(low[v] \ >= \ dfn[u]\) ，那么 \(u\) 点即为割点

为什么呢？

因为 \(low[v]\) 的定义为通过回边连出去的最小编号，则若 \(low[v]\) 小于 当前 \(u\) 的编号的话，那么将 \(u\) 点删掉， \(v\) 点照样可以通过 \(low[v]\) 这条边连出去，而形成连通；但若 \(low[v]\) 所连出去的边最小也还比 \(u\) 大，意思就是还是在 \(u\) 的子树中，那么一旦删去了 \(u\) ，则 \(v\) 将无法连通，即 \(u\) 为割点

Code

void tarjan(int u, int fa)//fa只是一个用来判断是否是根节点的变量
{
    dfn[u] = low[u] = ++ num;//dfs树的初值
    int son = 0;
    for(int i = head[u]; i; i = next[i])
    {
        int v = ver[i];
        if(! dfn[v])
        {
            tarjan(v, fa);
            low[u] = min(low[u], low[v]);
            if(u != fa) ans[u] = low[v] >= dfn[u] ? 1 : ans[u];
            else ++ son; //如果是根节点则记录儿子数
        }
        low[u] = min(low[u], dfn[v]);//若 v 是已经到过的点，即 (u, v) 为回边，那么 u 就是可以连到 v 的，即如此更新
    }
    if(u == fa) ans[u] = son >= 2 ? 1 : ans[u];
}