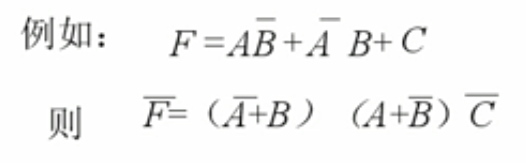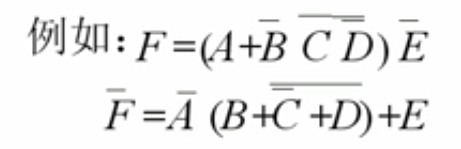【数电专栏】

B 逻辑函数及其描述

B.a 逻辑函数的基本概念

普通代数中的函数： $Y=A\times B+C$
左边是因变量，右边是自变量

逻辑代数中的函数： $Y=AB+C$
左边是输出变量，右边是输入变量

两者区别：

• 变量取值范围不同，输入和输出逻辑变量取值只能是0或1。
• 运算不同，逻辑代数是与运算，或运算，非运算。

<1> 逻辑函数的一般定义：设某一逻辑电路的输入逻辑变量为 $A_1、A_2、...、A_n$,输出逻辑变量为 $F$，如图所示。如果当 $A_1、A_2、...、A_n$的值确定后， $F$的值就唯一的被确定下来，则 $F$被称为 $A_1、A_2、...、A_n$的逻辑函数，记为 $F=f(A_1、A_2、...、A_n)$。
例子：加油站油罐液位控制系统
有两台一大一小电动机 $M_L$和 $M_S$驱动油泵向油罐注油。当油罐的液体位低于A点高于B点时由小电动机 $M_S$单独驱动；当液位在B点和C点之间时，由大电动机 $M_L$单独驱动；当液位在C点以下是，由两台电动机同时驱动。试设计控制该电动机工作的逻辑电路。
液位 $A、B、C$输入逻辑变量电动机 $M_S和M_L$为输出逻辑变量，液位低于 $A、B、C$某点时，用1表示，否则用0表示 $M_S和M_L$工作时用1表示，0表示不工作。
液位控制真值表：

逻辑函数：
$M_S=A\bullet \overline{B}\bullet\overline{C}+A\bullet B\bullet C$（100+111）
$M_L=A\bullet B\bullet\overline{C}+A\bullet B\bullet C$（110+111）
逻辑电路：

B.b 逻辑函数的描述方法

文字描述，真值表，逻辑函数表达式，逻辑电路图，卡诺图

（1）逻辑真值表

由于每个逻辑变量只能有0和1两种可能的取值，因此，n个逻辑变量只能有 $2^n$中取值组合。

（2）逻辑函数式

是把输出与输入之间的逻辑关系写成与、或、非等运算的组合式，即逻辑代数式。例如：
$F=f(A,B)=A\overline{B}+\overline{A}B$

（3）逻辑图
逻辑图就是用逻辑符号表示逻辑函数中各变量之间的与、或、非运算的逻辑电路图。

B.c逻辑函数各种表示方法间的相互转换

（1）逻辑函数表达式 $\iff$真值表

1）逻辑函数表达式 $\longrightarrow$真值表
首先，将n个变量的 $2^n$种0、1状态组合按二进制数按顺序填写到真值表的左边一栏。
然后将每一行的变量值代入逻辑表达式，算出输出逻辑值，记入右边一栏中
例：
$F=A\overline{B}+\overline{A}B$

2）逻辑函数表达式 $\longleftarrow$真值表
第一步 在真值表上找出输出1的行
第二步 将这一行中所有自变量写成与项，并且当变量的值为“1”时写成原变量 $A$，当变量对应的值为“0”写为反变量 $\overline{A}$。
第三步 将所有乘积项逻辑加，便得到逻辑函数表达式
例：

$\overline{A}\ \overline{B}C\qquad\overline{A}B\overline{C}\qquad A\overline{B}\ \overline{C}\qquad ABC$
$F=\overline{A}\ \overline{B}C+\overline{A}B\overline{C}+A\overline{B}\ \overline{C}+ABC$

（2）逻辑函数表达式 $\iff$逻辑电路图

1）逻辑电路图 $\longrightarrow$逻辑表达式
第一步 逐级写出逻辑函数表达式
第二步 最后写出输出端的逻辑函数表达式
例子：

2）逻辑表达式 $\longrightarrow$逻辑电路图

C 逻辑代数的运算法则

C.a 逻辑函数的相等

设有两个逻辑函数
$F_1=f_1(a_1，a_2，...，a_n)$
$F_2=f_2(a_1，a_2，...，a_n)$
若两逻辑函数具有完全相同的真值表，则这两个逻辑函数相等。真值表法是判断逻辑函数相等关系的最基本方法。此外，也可用逻辑代数的定理、规则和公式进行证明。

C.b逻辑代数的基本定律

（1）基本公式：

1）0-1律
$1\cdot A=A$ （常闭合的开关与A串联，结果完全取决于A ）
$0+A=A$ （常断开的开关与A并联，结果完全取决于A ）
$0\cdot A=A$（常断开的开关与A串联，结果永远是断开的）
$1+A=1$（常闭合的开关与A并联，结果永远是通的））

2）交换律：
$A\cdot B=B\cdot A$
$A+B=B+A$

3)结合率
$A\cdot (B\cdot C)=(A\cdot B)\cdot C$
$A+(A+B)=(A+B)+C$

4）分配律：
$A\cdot(B+C)=A\cdot B+A\cdot C$
$A+(B\cdot C)=(A+B)(A+C)$

5）互补律：
$A+\overline{A}=1$
$A\cdot \overline{A}=0$

6）重叠率：
$A\cdot A=A$
$A+A=A$

7） 还原率：
$\overline{\overline{A}}=A$

（2）常用公式

8）反演率：也称为摩根定理
$\overline{A\cdot B}=\overline{A}+\overline{B}$
$\overline{A+B}=\overline{A}\cdot \overline{B}$

9）吸收率( $I$)：
$A+AB=A$
$A(A+B)=A$

10)吸收律（ $II$）
$A+\overline{A}B=A+B$
$A(\overline{A}+B)=AB$

11)吸收律（ $III$）
$AB+A\overline{B}=A$
$(A+B)(A+\overline{B})=A$

12）冗余定律：冗余定律也成为多余项定理
$AB+\overline{A}C+BC=AB+\overline{A}C$
$(A+B)(\overline{A}+C)(B+C)=(A+B)(\overline{A}+C)$

C.c 逻辑代数的三个基本规则

（1）代入规则

代入规则指出，将逻辑等式中的某一变量代以另一函数，其等式仍然成立。
例如：利用代入规则可以证明:
$\overline{A+C+D}=\overline{A}\ \overline{C}\ \overline{D}$
令 $A+C=M,\\ \overline{M+D}=\overline{M}\cdot \overline{D} =\overline{A+C}\cdot \overline{D} =\overline{A}\ \overline{C}\ \overline{D}$

（2）对偶规则

将原函数式 $F=f(A,B,...)$中的所有 $"\cdot"$变为 $"+"$， $“+”$变为 $"\cdot"$,0变为1，1变为0,所有变量不变，这样得到的新函数，叫原函数式的对偶式 $F'$。

注意：

• 由原式求对偶式时，原来的运算顺序保持不变。要正确运用括号来表示运算顺序，原来先运算的仍然要先运算。
• 求对偶式时，原式中的长短非号一律保持不变。
• $F和F'$互为对偶，显然，某逻辑函数的对偶便为原函数，即 $(F')'=F$。

例子：

注：基本公式同一定律的两个式子为对偶式。

（3）反演规则

从原函数求反函数的过程叫做反演。将原函数式 $F=f(A,B,...)$中的所有 $"\cdot"$变为 $"+"$， $“+”$变为 $"\cdot"$,0变为1，1变为0，原、反变量互变，这样得到的新函数 $\overline{F}$叫函数式的反函数。
例子:

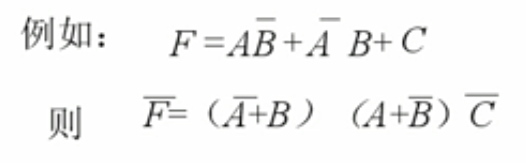
注意：

• 反演时，原来的运算顺序应保持不变。原式中要先运算的仍要先运算。
• 反演过程中，多个变量上面的长非号没有变，但长非号下面的每个变量都变了。
• 例子：
• 

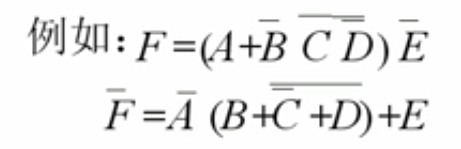
小结：至此，我们定义了五种逻辑符号： $0、1、\cdot 、+、-$，确定了基本定律（基本公式）和常用公式。三个基本规则，它们构成了整个逻辑代数系统。任何逻辑问题均可用它们来描述、推导和变换，这些都是学习数字逻辑电路最起码的基础知识。