1、问题
最小生成树算法(MST),分别用prim和kruskal算法实现。
最小生成树:一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。----百度百科
通俗来讲,最小生成树就是在原有图上,选择n-1条边,抛弃未选择的边,使得所有n个结点都是连通的,并且这n-1条边的权值和最小。由n个点,n-1条边,易得出这是一棵树,同权值和最小这个要 求,组成了“最小生成树”的名称。
2、解析
MST主要有两种方法。
1、Prim算法
①.任意选择一点A作为源点。将其标记,表示加入集合a。
②.选择离集合a最近的点B,标记,加入集合a,权值和ans+=权值。
③.在B加入集合a后,要将未标记的点与集合的最小距离更新。
④.重复执行②与③步骤,直到没有点未被标记或已到达n个点结束。
⑤.若被标记的点小于n,则该图不连通;若等于n,则MST存在,且权值和为ans
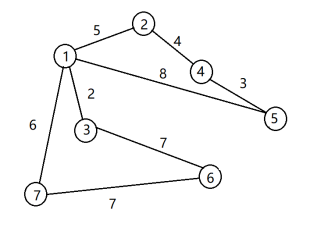
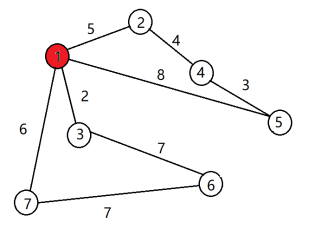
(1)原图 (2) 1作为源点,加入集合a
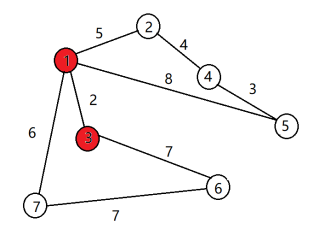
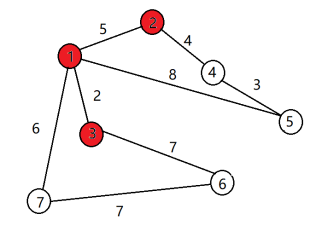
(3) 结点3离集合a最近,加入集合a,ans+=2 (4)同理,2加入集合a,ans+=5
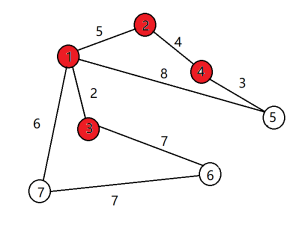

(5)同理,4加入集合a,ans+=4 (6)同理,5加入集合a,ans+=3
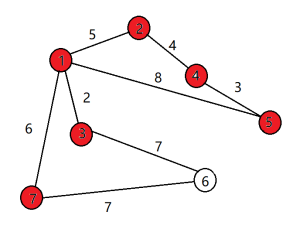
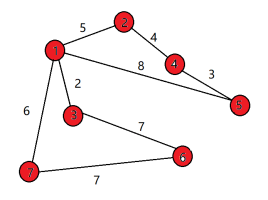
(7) 同理,7加入集合a,ans+=6 (8)同理,6加入集合a,ans+=7
至此,所以7个点都加入了集合a中,选择了n-1条边,ans=27。算法结束。
2、Kruscal算法
①.将所以的边权,由小到大排列,创建空的边集合a。
②.从第一条边开始遍历,若此边加入集合a后会构成环,则跳过检查下一条边,否则加入集合a中,ans+=权值。
③.若成功加入n-1条边,则权值和则为ans;否则证明此图不连通。
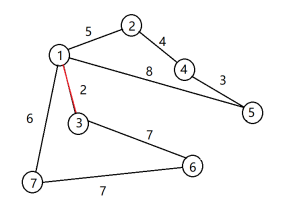
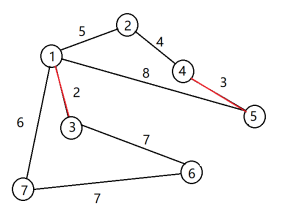
(1) 加入e(1,3),ans+=2 (2)加入e(4,5),ans+=3
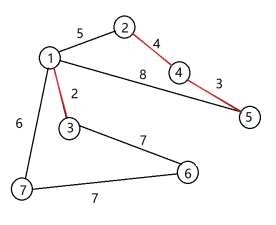
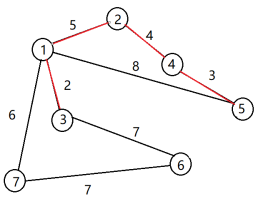
(3)加入e(2,4),ans+=4 (4)加入e(1,2),ans+=5
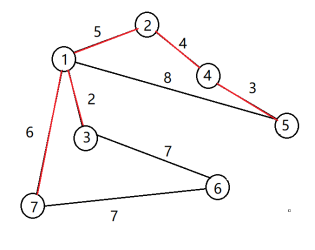
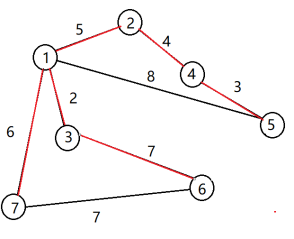
(5)加入e(1,7),ans+=6 (6)加入e(3,6),ans+=7
至此,n-1条边都加入到了集合a中,ans=27。算法结束。
2、设计
1、Prim算法
此算法的时间复杂度重点在于如何快速取出离集合最近的点。因此我们可以用堆优化的方法降低时间复杂度。
//采用堆优化后的伪代码 memset(dis,127,sizeof(dis)); while(队列非空&&加入点的个数<n) { 若此节点被访问过则continue; 标记此节点; ans+=weight; ++cnt; for(链式前向星存图,遍历此节点的边) { int to=下一个节点; if(weight<dis[to]) { dis[to]=weight; push(make_pair(dis[to],to)); } } } if(cnt==n)cout<<”权值和为”<<ans<<”\n”; else cout<<”此图不连通”<<”\n”;
2、Kruscal算法
此算法的重难点在于如何判断新加入的边是否会与原集合构成环,可以用并查集来检查,检查边两点是否有公共祖先。
//p[i]数组保存i的祖先 int find(int x) { //找到x点的祖先 if(x==p[x])return x; else return p[x]=find(p[x]); } //将x与y合并 void join(int x,int y) { int a=find(a),b=find(y); p[a]=b; } void kruscal() { 将边从小到大排序; for(遍历边) { 若边的两节点属于同一集合,continue; join(两节点); ans+=weight; ++cnt; } } if(cnt==n-1)cout<<”权值和为”<<ans<<”\n”; else cout<<”此图不连通”<<”\n”;
4、分析
1、Prim算法
对于普通的解法,根据原理,for的范围是1至n-1,为O(n)的复杂度。for里还有两层单独的for语句,第一层为找到最近的点,复杂度为O(n);第一层为更新各个未遍历的点离集合的最小距离,若未经过存储优化,也有O(n)的复杂度,综上,朴素时间复杂度为O(n²)。
但我加入了pair、priority_queue以及链式前向星存图,我们知道队列的操作为log(n),因此找点的复杂度为log(n),更新操作最多遍历m次边,复杂度为O(m),综上,堆优化的时间复杂度被降低至mlog(n)。
2、Kruscal算法
易得第一层for循环最多遍历m条边,复杂度为O(m);并查集查找祖先与合并的操作分析比较复杂,我从网上查阅得知复杂度为,而外层还有个一个sort函数,复杂度为O(mlog(m)),综上,时间复杂度为O(mlog(m))。
5、源码
Prim算法
/* author: keke project name:Prim算法(堆优化) Time Complexity: O(mlog(n)) */ #include<bits/stdc++.h> using namespace std; #define pi acos(-1.0) #define inf 0x3f3f3f3f typedef long long ll; typedef unsigned long long ull; typedef double db; int mo[4][2] = { -1,0,1,0,0,-1,0,1 }; //int mo[8][2] = { -1,0,1,0,-1,-1,1,1,0,-1,0,1,1,-1,-1,1 }; const int maxn = 2e5 + 10; int n, m, ans, head[maxn], cnt, dis[5010], sum; bool vis[maxn]; struct xx {//链式前向星存图 int t, next, w; }xx[maxn << 1]; void add(int a, int b, int c) {//添加边 xx[cnt].next = head[a]; xx[cnt].t = b; xx[cnt].w = c; head[a] = cnt++; } priority_queue<pair<int, int> >q; void solve(int x) { memset(dis, 127, sizeof(dis));//初始化为很大的数 dis[x] = 0;//设置源点的dis为0 q.push(make_pair(0, 1)); while (!q.empty() && sum < n) { int a = q.top().first, b = q.top().second; q.pop(); if (vis[b])continue; vis[b] = true; ++sum, ans -= a;//a为负数 for (int i = head[b]; ~i; i = xx[i].next) { int to = xx[i].t; if (xx[i].w < dis[to]) { dis[to] = xx[i].w; q.push(make_pair(-dis[to], to));//加个'-',大根堆变小根堆 } } } } int main() { #ifdef ONLINE_JUDGE #else freopen("input.txt", "r", stdin); #endif ios::sync_with_stdio(0); cin.tie(0), cout.tie(0); cout << fixed << setprecision(2); memset(head, -1, sizeof(head)); cin >> n >> m; while (m--) { int a, b, c; cin >> a >> b >> c; add(a, b, c); add(b, a, c);//无向图,需要反向加边 } solve(1);//设置节点1为源点 if (sum == n)cout << ans << "\n"; else cout << "orz" << "\n"; return 0; //good job! }
Kruscal
/* author: keke project name:Kruscal算法 Time Complexity: O(mlog(m)) */ #include<bits/stdc++.h> using namespace std; #define pi acos(-1.0) #define inf 0x3f3f3f3f typedef long long ll; typedef unsigned long long ull; typedef double db; int mo[4][2] = { -1,0,1,0,0,-1,0,1 }; //int mo[8][2] = { -1,0,1,0,-1,-1,1,1,0,-1,0,1,1,-1,-1,1 }; const int maxn = 2e5 + 10; int n, m, is, t, ans, p[5010], cnt; struct xx {//存边 int f, t, w; }xx[maxn]; int find(int x) {//并查集查找祖先,维护集合问题 if (x == p[x])return x; else return p[x] = find(p[x]); } bool cmp(struct xx a, struct xx b) { return a.w < b.w; }//权值从小到大 void solve() { sort(xx + 1, xx + 1 + m, cmp); int sum = 0;//计加入的边数 for (int i = 1; i <= m; i++) { int a = find(xx[i].f), b = find(xx[i].t); if (a != b) {//若不会构成环,则将这条边加入集合 p[a] = b; ++sum, ans += xx[i].w; } if (sum == n - 1)break; } if (sum == n - 1)cout << ans << "\n"; else cout << "orz" << "\n"; } int main() { #ifdef ONLINE_JUDGE #else freopen("input.txt", "r", stdin); #endif ios::sync_with_stdio(0); cin.tie(0), cout.tie(0); cout << fixed << setprecision(2); cin >> n >> m; for (int i = 1; i <= n; i++)p[i] = i; for (int i = 1; i <= m; i++) { cin >> xx[i].f >> xx[i].t >> xx[i].w; } solve(); return 0; //good job! }