一、特征值的界估计
定义1：若n阶复数矩阵A=(aij)m*n的特征值的集合（A的谱）为{λ1，λ2，.....，λn}，则有不等式
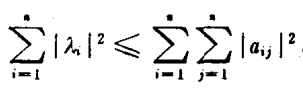当且仅当A为正规矩阵时等号成立；
二、圆盘定理
圆盘定理用于对矩阵的特征值在复数平面上的位置做出准确的估计；
定理2：设A=(aij)为任一n阶复数矩阵，则A的特征值都在复数平面的n个圆盘
|z-aii|<=Ri （i为自然数集合，aii是矩阵对角线元素）的并集内部，这里的Ri为
Ri=|ai1|+|ai2|+.....+|ain|；（第i行所有元素的之和），上述的圆盘|z-aii|<=Ri称为盖儿圆，此定理表明对于矩阵A的任一特征值λ，
总存在盖儿圆Si，使得λ属于Si.。
注：此定理仅仅是说明了矩阵A的特征值落在A的n个盖儿圆的并集内部，并未指出是在那个圆盘中有多少个特征值；
定理2：矩阵A的任一由k个盖儿圆组成的连通部分里面，有且只有A的k个特征值（当A的主对角线上有相同元素时，按照
重复次数计算，有相同特征值时亦需要按照重复次数计算）
三、谱半径的估计
定义：谱半径就是矩阵A所有特征值中模的最大值；
定理1：复数域上的任一n阶方阵A的谱半径都不超过A的范数||A||；此处的||A||为任一方阵范数
定理2：如果A是正规矩阵，则谱半径等于A的第二范数||A||2；
第一个推论：通过列元素求和，取列值和的最大值；
第二个推论：通过行元素求和，取行值和的最大值；
对于第三个推论中：
四、广义逆矩阵与线性方程组的解
定义1：设A是一个n*m的矩阵，一个n*m的矩阵G称为A的一个{1}-广义逆，如果对任意给出的m*1矩阵B，只要方程组AX=B
有解，则X=GB也一定是解；
定理1：n*m矩阵G是m*n矩阵A的一个1{}-广义逆，当且仅当AGA=A；
A的{1}-广义逆为n*m阶，X为r*(m-r)矩阵，Y为(n-r)*r矩阵，Z为(n-r)*(m-r)矩阵；//可进行简单推导
注：由上述定义可知对于任意m*n矩阵A，其{1}-广义逆总是存在，即A{1}总是非空，又由XYZ的任意性可知广义逆并不唯一；
定理：若G是m*n矩阵A的一个{1}-广义逆，AX=B有解时，其通解可以表示为X=GB+（E-GA）Z，Z为任意n维列向量。
定理：设G为m*n矩阵A的一个{1}-广义逆，并且（GA）^H=（GA）（即GA为正规阵）那么对任给的m维列向量B，只要
AX=B有解，则X=GB就是其最小范数解；
定理：若G是m*n矩阵A的一个{1}-广义逆，并且（AG）^H=（AG）（即GA为正规阵）那么对任给的m维列向量B，只要
AX=B有解，则X=GB就是其最小二乘解；
定义：设A为任一m*n矩阵，如果n*m矩阵G满足Moore-Penrose方程
1）AGA=A 2）GAG=G 3）（GA）^H=（GA） 4）（AG）^H=（AG）的一部分或者全部，则称G为A的广义逆矩阵。
满足条件1的广义逆矩阵就是{1}-广义逆，记做A{1}；
满足全部四个条件的广义逆矩阵记为A{1,2,3,4}，这一类广义逆对于给定的A来说，有且只有唯一的一个广义逆与之对应，
记为A+，并称之为M-P广义逆；
五、广义逆矩阵A+
定理：设A是m*n矩阵，则M-P广义逆矩阵A+存在且唯一，即同时满足以下条件
1）AGA=A 2）GAG=G 3）（GA）^H=（GA） 4）（AG）^H=（AG）的n*m矩阵G存在且唯一，记做A+；
常用的广义逆矩阵求解公式：
对于行列满秩的情况下：
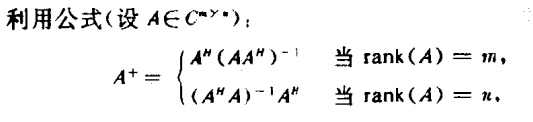
对于一般情况下（极限求解）：
A^H为其共轭转置矩阵，如果A矩阵为实数阵就是A的转置矩阵（对于共轭复数即实部相等，虚部互为相反数）；
M-P广义逆矩阵A+的性质：
（A+）+=A （AA+）^2=AA+ （A^H）+=（A+）^H
