决策树

决策树是一种基于规则的方法，它用一组嵌套的规则进行预测。在树的每个决策节点处，根据判断结果进入一个分支，反复执行这种操作直到到达叶子节点，得到预测结果。这些规则是通过训练得到的，而不是人工制定的。 ————《机器学习与应用》雷明

其实在我看来，本质上，它就是从一层层的if/else 问题中进行学习，并得出结论。

$Eg$ : 你想要区分下面的四种动物：熊、鹰、企鹅和海豚
你的目标是通过提出尽可能少的if/else问题来得到正确答案。你可能会提出类似与下图的问题：
在这里插入图片描述

决策树是一种通过对特征属性的分类对样本进行分类的树形结构，包括有向边与三类节点：

根节点（root node），表示第一个特征属性，只有出边没有入边；上例中的：有没有羽毛
内部节点（internal node），表示特征属性，有一条入边至少两条出边：上例中的：会不会飞？有没有鱼鳍？
叶子节点（leaf node），表示类别，只有一条入边没有出边。上例中的：企鹅、海豚等。

ID3

ID3算法是决策树的一种，它是基于奥卡姆剃刀原理的，即用尽量用较少的东西做更多的事。ID3算法，即Iterative Dichotomiser 3，迭代二叉树3代，是Ross Quinlan发明的一种决策树算法，这个算法的基础就是上面提到的奥卡姆剃刀原理，越是小型的决策树越优于大的决策树，尽管如此，也不总是生成最小的树型结构，而是一个启发式算法。

在信息论中，期望信息越小，那么信息增益就越大，从而纯度就越高。ID3算法的核心思想就是以信息增益来度量属性的选择，选择分裂后信息增益最大的属性进行分裂。该算法采用自顶向下的贪婪搜索遍历可能的决策空间。

信息熵与信息增益

在信息增益（Information gain）中，重要性的衡量标准就是看特征能够为分类系统带来多少信息，带来的信息越多，该特征越重要。在认识信息增益之前，先来看看信息熵的定义

熵（entropy）这个概念最早起源于物理学，在物理学中是用来度量一个热力学系统的无序程度，而在信息学里面，熵是对不确定性的度量。在1948年，香农引入了信息熵(Information entropy)，将其定义为离散随机事件出现的概率，一个系统越是有序，信息熵就越低，反之一个系统越是混乱，它的信息熵就越高。所以信息熵可以被认为是系统有序化程度的一个度量。

信息的大小跟随机事件的概率有关。越小概率的事情发生了产生的信息量越大，如湖南产生的地震了；越大概率的事情发生了产生的信息量越小，如太阳从东边升起来了（肯定发生嘛，没什么信息量）。

假如一个随机变量 $X$ 的取值为 $X=(x_1,x_2,...,x_n)$ ，每一种取到的概率分别是 $(p_1,p_2,...,p_n)$ ，那么 $X$ 的熵定义为

$E(X)=-\sum_{i=1}^np_ilog_2p_i（当对数的底为2时，熵的单位为bit；为e时，单位为nat。）$

同理对于连续随机变量Y，其熵可定义为

$E(Y)=-\int_{-\infty}^{+\infty}f(y)log_2f(y)dy$

当给定随机变量 $X$ 的条件下随机变量 $Y$ 的熵可定义为条件熵 $H(Y|X)$ :

$E(Y|X)=-\sum_{i=1}^np_iE(Y| X=x_i)$

意思是一个变量的变化情况可能越多，那么它携带的信息量就越大。

所谓信息增益就是数据在得到特征X的信息时使得类Y的信息不确定性减少的程度。假设数据集D的信息熵为 $E(D)$ ,给定特征A之后的条件熵为 $E(D|A)$ ,则特征A对于数据集的信息增益 $g(D,A)$ 可表示为：

$g(D,A)=E(D)-E(D|A)$

信息增益越大，则该特征对数据集确定性贡献越大，表示该特征对数据有较强的分类能力。

接下来以天气预报的例子来说明。下面是描述天气数据表，学习目标是play或者not play。

humility	outlook	play	temp	windy
high	sunny	no	hot	false
high	sunny	no	hot	true
high	overcast	yes	hot	false
high	rainy	yes	mild	false
normal	rainy	yes	cool	false
normal	rainy	no	cool	true
normal	overcast	yes	cool	true
high	sunny	no	mild	false
normal	sunny	yes	cool	false
normal	rainy	yes	mild	false
normal	sunny	yes	mild	true
high	overcast	yes	mild	true
normal	overcast	yes	hot	false
high	rainy	no	mild	true

可以看出标签Play中一共14个样例，包括9个正例和5个负例。

计算目标特征的信息熵

$E_{Play}=E(5,9)=E(0.36,0.64)=-(0.36log_20.36)-(0.64log_20.64)=0.94$
计算加入某个特征后的条件熵

$E(Y|X)=-\sum_{i=1}^np_iE(Y| X=x_i)$ [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KNzs0y12-1582361735135)(C:\Users\xiang0712\AppData\Roaming\Typora\typora-user-images\image-20200220182203003.png)]

$E(Play|outlook)=P(Sun)*E(3,2)+P(Ove)*E(4,0)+P(Rai)*E(2,3)$

$=(5/14)*0.97+(4/14)*0+(5/14)*0.97=0.69$
计算信息增益
$g(D,A)=E(D)-E(D|A)$
$g(Play,outlook)=E_{play}-E(Paly|outlook)=0.94-0.69=0.25$

同理计算其他特征得信息增益为：

$g(Play,temp)=0.15$
$g(Play,humidity)=0.05$
$g(Play,windy)=0.03$

所第一个结点应该为 $Outlook$ ,因为它的信息增益最大。在依次计算下面的结点。

最终得如下的决策树：

在决策树的每一个非叶子结点划分之前，先计算每一个属性所带来的信息增益，选择最大信息增益的属性来划分，因为信息增益越大，区分样本的能力就越强，越具有代表性，很显然这是一种自顶向下的贪心策略。以上就是ID3算法的核心思想。

代码实现

"""
ID3-->
    |-->entroy()   计算熵
    |-->split_dataframe 分离数据
    |-->choose_best_col  选择最好的属性（信息增益）
    |-->choose_best_gainratio    信息增益率
    |-->ID3Tree
       |-->Node    存储结点
          |-->connect
	   |-->print_tree
	   |-->construct_tree  创建决策树
	      |-->construct

"""


import numpy as np
import numpy as np
import pandas as pd
from math import log


def entropy(ele):
    """
    set(ele)
    {'yes', 'no'}
    """
    probs = [ele.count(i) / len(ele) for i in set(ele)]
    entropy = -sum([prob * log(prob, 2) for prob in probs])
    return entropy

def split_dataframe(data, col):
    unique_values = set(data[col])
    result_dict = {elem: pd.DataFrame for elem in unique_values}
    for key in result_dict.keys():
        result_dict[key] = data[:][data[col] == key]
    return result_dict
#选择最好的属性
def choose_best_col(data, label):
    entropy_D = entropy(data[label].tolist())
    print("目标特征%s的信息熵：%lf"%(label,entropy_D))
    """
    data[play].tolist()
    ['no', 'no', 'yes', 'yes', 'yes', 'no', 'yes', 'no', 'yes', 'yes', 'yes', 'yes', 'yes', 'no']
    """
    cols = [col for col in data.columns if col not in [label]]
    max_value, best_col = 0, None
    max_splited = None
    for col in cols:
        splited_set = split_dataframe(data, col)
        entropy_DA = 0
        for subset_col, subset in splited_set.items():
            entropy_Di = entropy(subset[label].tolist())
            entropy_DA += len(subset) / len(data) * entropy_Di
        info_gain = entropy_D - entropy_DA
        print("特征%s的信息增益为%lf"%(col,info_gain))
        if info_gain > max_value:
            max_value, best_col = info_gain, col
            max_splited = splited_set
    print("最好的特征：%s\n"%best_col)
    return max_value, best_col, max_splited


class ID3Tree:
    #生成结点
    class Node:
        def __init__(self, name):
            self.name = name
            self.connections = {}

        def connect(self, label, node):
            self.connections[label] = node

    def __init__(self, data, label):
        self.columns = data.columns
        self.data = data
        self.label = label
        self.root = self.Node("Root")
	#打印结果
    def print_tree(self, node, tabs):
        print(tabs + node.name)
        for connection, child_node in node.connections.items():
            print(tabs + "\t" + "(" + connection + ")")
            self.print_tree(child_node, tabs + "\t\t")
	#创建决策树
    def construct_tree(self):
        self.construct(self.root, "", self.data, self.columns)

    def construct(self, parent_node, parent_connection_label, input_data, columns):
        max_value, best_col, max_splited = choose_best_col(input_data[columns], self.label)

        if not best_col:
            node = self.Node(input_data[self.label].iloc[0])
            parent_node.connect(parent_connection_label, node)
            return

        node = self.Node(best_col)
        parent_node.connect(parent_connection_label, node)

        new_columns = [col for col in columns if col != best_col]

        for splited_value, splited_data in max_splited.items():
            self.construct(node, splited_value, splited_data, new_columns)


df = pd.read_csv('example.csv', dtype={'windy':'str'})
print("数据集")
print(df)
id3 = ID3Tree(df, "Play")
id3.construct_tree()
id3.print_tree(id3.root, '')

运行结果

Root
	()
		outlook
			(overcast)
				yes
			(sunny)
				humility
					(normal)
						yes
					(high)
						no
			(rainy)
				windy
					(false)
						yes
					(true)
						no

C4.5

C4.5是在ID3决策树的基础之上稍作改进的

它克服了ID3 的两个缺点：

用信息增益选择属性时偏向于选择分枝比较多的属性值，即取值多的属性
不能处理连贯（连续）属性

在ID3中选择最优子结点是用的信息增益来作比较，这样就会出现选择是会偏向选择分枝比较多的属性值；而C4.5在选择最优的子结点时，使用的是信息增益率。

信息增益率

增益率（Gain Ratio)是可以作为选择最优划分属性的方法，增益率的计算公式为：
${gain\_ratio(D,A)}=\frac {g(D,A)}{E(A)}=\frac {E(D)-E(D|A)}{E(A)}$

代码实现

因为这里是改进ID3的算法，而且就是选择最优属性的时候改变了，所以我们只需改变函数choose_best_col即可

#再声明一个函数
# C4.5 算法，比较信息增益率
def choose_best_gainratio(data, label):
    entropy_D = entropy(data[label].tolist())
    print("目标特征%s的信息熵：%lf"%(label,entropy_D))
    """
    data[play].tolist()
    ['no', 'no', 'yes', 'yes', 'yes', 'no', 'yes', 'no', 'yes', 'yes', 'yes', 'yes', 'yes', 'no']
    """
    cols = [col for col in data.columns if col not in [label]]
    max_value, best_col = 0, None
    max_splited = None
    for col in cols:
        splited_set = split_dataframe(data, col)
        entropy_DA = 0
        entropy_A=0
        for subset_col, subset in splited_set.items():
            entropy_Di = entropy(subset[label].tolist())
            entropy_DA += len(subset) / len(data) * entropy_Di
        entropy_A =entropy(data[col].tolist())
        if entropy_A!=0:
            info_gain_ratio = (entropy_D - entropy_DA)/entropy_A
        else:
            info_gain_ratio=0
        print("特征%s的信息增益率为%lf"%(col,info_gain_ratio))
        if info_gain_ratio > max_value:
            max_value, best_col = info_gain_ratio, col
            max_splited = splited_set
    print("最好的特征：%s\n"%best_col)
    return max_value, best_col, max_splited

部分计算过程

目标特征play的信息熵：0.940286
特征humility的信息增益率为0.151836
特征outlook的信息增益率为0.156428
特征temp的信息增益率为0.018773
特征windy的信息增益率为0.048849
最好的特征：outlook

目标特征play的信息熵：0.970951
特征humility的信息增益率为0.020571
特征temp的信息增益率为0.020571
特征windy的信息增益率为1.000000
最好的特征：windy

目标特征play的信息熵：0.970951
特征humility的信息增益率为1.000000
特征temp的信息增益率为0.375150
特征windy的信息增益率为0.020571
最好的特征：humility

目标特征play的信息熵：-0.000000
特征humility的信息增益率为-0.000000
特征temp的信息增益率为-0.000000
特征windy的信息增益率为-0.000000
最好的特征：None

最终结果

Root
	()
		outlook
			(rainy)
				windy
					(false)
						yes
					(true)
						no
			(overcast)
				yes
			(sunny)
				humility
					(normal)
						yes
					(high)
						no

可以看出这里的决策树与ID3算法得出的决策树是一样的

CART

分类与回归树（Classification and Regression Trees, CART）是由四人帮Leo Breiman, Jerome Friedman, Richard Olshen与Charles Stone于1984年提出，既可用于分类也可用于回归。

Gini不纯度

这里是使用Gini不纯度的值来做为选择最佳属性的条件：

$Gini不纯度： Gini(D)=1-\sum_iP_i^2=1-\frac{\sum_iN_{i}^2}{N^2}$

当样本属于某一类时Gini不纯度的值最小，此时最小值为0；当样本均匀分布于每一类时Gini不纯度的值最大。

上面定义的是样本集的不纯度，我们需要评价的是分裂的好坏，因此，需要根据样本集的不纯度构造出分裂的不纯度。分裂规则将节点的训练样本集分裂成左右两个子集，分裂的目标是把数据分成两部分之后这两个子集都尽可能纯。因此，我们计算左右子集的不纯度之和作为分裂的不纯度，显然求和需要加上权重，以反映左右两边的训练样本数。由此得到分裂的不纯度计算公式为

$G=\frac {N_L}{N}G(D_L)+\frac{N_R}{N}G(D_R)$

其中， $G(D_L)$ 是左子集的不纯度； $G(D_R)$ 是右子集的不纯度； N 是总样本数； $N_L$ 是左子集的样本数；$ N_R $是右子集的样本数。

如果采用 Gini 不纯度指标，将 Gini 不纯度的计算公式代人上式可以得到

$G=\frac {N_L}{N}\left(1-\frac{\sum_iN_{L,i}^2}{N_L^2} \right)+\frac{N_R}{N}\left(1-\frac{\sum_iN_{R,i}^2}{N_L^2} \right)$
$=\frac{1}{N}\left(N_L-\frac{\sum_iN_{L,i}^2}{N_L}+N_R-\frac{\sum_iN_{R,i}^2}{N_R} \right)$

$=1-\frac1N\left(\frac{\sum_iN_{L,i}^2}{N_L}+ \frac{\sum_iN_{R,i}^2}{N_R}\right)$

由于 N 是常数，要让 Gini 不纯度最小化等价于让下面的值最大化：

$G=\frac{\sum_iN_{L,i}^2}{N_L}+ \frac{\sum_iN_{R,i}^2}{N_R}$

这个值可以看作 Gini 纯度，它的值越大，样本越纯。寻找最佳分裂时需要计算用每个阈值对样本集进行分裂后的这个值，寻找该值最大时对应的分裂，它就是最佳分裂。

如果是数值型特征，对于每个特征将 $l$ 个训练样本按照该特征的值从小到大排序，假设排序后的值为 $x_1,x_2,....,x_l$

接下来从 $x_1$ 开始，依次用每个 $x_i$ 作为阈值，将样本分成左右两部分，计算上面的纯度值，该值最大的那个分裂阈值就是此特征的最佳分裂阈值。在计算出每个特征的最佳分裂阈值和上面的纯度值后，比较所有这些分裂的纯度值大小，该值最大的分裂为所有特征的最佳分裂。这里采用贪心法的策略，每次都是选择当前条件下最好的分裂作为当前节点的分裂。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-481k4fBO-1582361735136)(C:\Users\xiang0712\AppData\Roaming\Typora\typora-user-images\image-20200222164132382.png)]
对于回归树，衡量分裂的标准是回归误差（即样本方差），每次分裂时选用使得方差最小化的那个分裂。假设节点的训练样本集有 $l$ 个样本（ $x_i,y_i$ ），其中， $x_i$ 为特征向量， $y_i$ 为实数的标签值。节点的回归值为所有样本的均值，回归误差为所有样本的标签值与回归值的均方和误差，定义为
$E(D)=\frac1l\sum_{i=1}^l(y_i-\vec{y})^2$
把均值的定义带入上式，得到
$E(D)=\frac1l\sum_{i=1}^l(y_i-\frac1l\sum_{j=1}^ly_i^2)^2$

根据样本集的回归误差，我们同样可以构造出分裂的回归误差。分裂的目标是最大程度地减小回归误差，因此，把分裂的误差指标定义为分裂之前的回归误差减去分裂之后左右子树的回归误差：

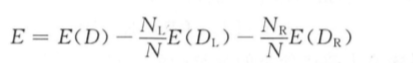
将误差的计算公式代入上式，可以得到

寻找最佳分裂时要计算上面的值，让该值最大化的分裂就是最佳分裂。回归树对类别型特征的处理和分类树类似，只是 E 值的计算公式不同，其他的过程相同。

引用

[1] Pang-Ning Tan, Michael Steinbach, Vipin Kumar, Introduction to Data Mining.
[2] Naren Ramakrishnan, The Top Ten Algorithms in Data Mining.
[3] 李航,《统计学习方法》.
[4] 雷明,《机器学习与应用》
[5] https://www.cnblogs.com/en-heng/p/5013995.html
[6] https://blog.csdn.net/u011067360/article/details/24871801
[7] https://github.com/luwill/machine-learning-code-writing

AU20190909

发布了20 篇原创文章 · 获赞 6 · 访问量 866

私信关注

Day6_决策树_ID3_C4.5_CART

决策树

ID3

信息熵与信息增益

代码实现

C4.5

信息增益率

代码实现

CART

Gini不纯度

引用

猜你喜欢